Trắc nghiệm Ôn tập chương 6 - Vật Lí 12Đề bài
Câu 1 :
Giới hạn quang điện của Cu là 300 nm. Công thoát của electron khỏi Cu là:
Câu 2 :
Các bức xạ trong dãy Banme thuộc vùng nào trong các vùng sau?
Câu 3 :
Kim loại dùng làm Catot của một tế bào quang điện có \(A{\rm{ }} = {\rm{ }}6,625{\rm{ }}eV\). Lần lượt chiếu vào catot các bước sóng: \({\lambda _1} = 0,1875\mu m\); \({\lambda _2} = 0,1925\mu m\); \({\lambda _3} = 0,1685\mu m\). Hỏi bước sóng nào gây ra được hiện tượng quang điện?
Câu 4 :
Động năng ban đầu cực đại của các e phụ thuộc vào?
Câu 5 :
Chiếu một chùm bức xạ đơn sắc vào một tấm kẽm có giới hạn quang điện \(0,35μm\) . Hiện tượng quang điện sẽ không xảy ra khi chùm bức xạ có bước sóng là
Câu 6 :
Theo quan điểm của thuyết lượng tử phát biểu nào sau đây là không đúng?
Câu 7 :
Công thoát của kim loại Na là 2,48 eV. Chiếu một chùm bức xạ có bước sóng \(0,36\mu m\) vào tế bào quang điện có catôt làm bằng Na thì cường độ dòng quang điện bão hoà là 3mA . Số êlectron bị bứt ra khỏi catôt trong mỗi giây là:
Câu 8 :
Phát biểu nào sau đây là ĐÚNG khi nói về quang phổ của nguyên tử H
Câu 9 :
Giới hạn quang điện của Na là \(0,50\mu m\). Chiếu vào Na tia tử ngoại có bước sóng \(\lambda = 0,25\mu m\). Vận tốc ban đầu cực đại của electron quang điện là:
Câu 10 :
Gọi \({\lambda _\alpha }\) và \({\lambda _\beta }\) lần lượt là 2 bước sóng của 2 vạch \(H{_\alpha }\) và \({H_\beta }\) trong dãy Banme. Gọi \({\lambda _1}\) là bước sóng của vạch đầu tiên trong dãy Pasen. Xác định mối liên hệ của \({\lambda _\alpha },{\lambda _\beta },{\lambda _1}\)
Câu 11 :
Chiếu ánh sáng đơn sắc có bước sóng \(320{\rm{ }}nm\) vào bề mặt ca tốt của một tế bào quang điện làm bằng xedi có giới hạn quang điện là \({\lambda _0} = 660nm\). Hiệu điện thế hãm của nó có giá trị là:
Câu 12 :
Dãy Laiman trong quang phổ vạch của Hiđrô ứng với sự dịch chuyển của các electron từ các quỹ đạo dừng có năng lượng cao về quỹ đạo:
Câu 13 :
Trong một tế bào quang điện có \({I_{bh}} = 2\mu A\) và hiệu suất lượng tử là \(0,5\% \). Số photon đến Ca tốt mỗi giây là:
Câu 14 :
Chiếu một bức xạ có bước sóng λ = 0, 48µm lên một tấm kim loại có công thoát A = 2,4.10-19J. dùng màn chắn tách ra một chùm hẹp các êlectron quang điện và hướng chúng bay theo chiều véc tơ cường độ điện trường có E = 1000 V/m. Quãng đường tối đa mà êlectron chuyển động được theo chiều véc tơ cường độ điện trường xấp xỉ là:
Câu 15 :
Cho giới hạn quang điện của catot là \({\lambda _0} = 660nm\) và đặt vào đó giữa Anot và Catot một \({U_{AK}} = {\rm{ }}1,5{\rm{ }}V\). Dùng bức xạ có \(\lambda = 330nm\). Động năng cực đại của các quang electron khi đập vào anot là:
Câu 16 :
Chiếu ánh sáng đơn sắc có bước sóng \(\lambda = 330nm\) vào bề mặt ca tốt của một tế bào quang điện hiệu điện thế hãm của nó có giá trị là \({U_h}\). Cho giới hạn quang điện của catot là \({\lambda _0} = 660nm\) và đặt vào đó giữa Anot và Catot một \({U_{AK}} = {\rm{ }}1,5{\rm{ }}V\). Tính động năng cực đại của các quang electron khi đập vào anot nếu dùng bức xạ \(\lambda ' = 282,5nm\):
Câu 17 :
Chiếu ánh sáng đơn sắc có bước sóng \(\lambda = 546{\rm{ }}nm\) vào bề mặt ca tốt của một tế bào quang điện, có \({I_{bh}} = {\rm{ }}2{\rm{ }}mA\). Công suất lượng tử là \(P{\rm{ }} = {\rm{ }}1,515{\rm{ }}W\). Tính hiệu suất lượng tử.
Câu 18 :
Năng lượng cần thiết để iôn hoá nguyên tử kim loại là 2,2eV. Kim loại này có giới hạn quang điện là:
Câu 19 :
Chiếu đồng thời hai bức xạ vào một tế bào quang điện, ta cần dùng các hiệu điện thế hãm để triệt tiêu dòng quang điện. Cho biết Uh1= 2Uh2. Hỏi có thể kết luận gì?
Câu 20 :
Kim loại dùng làm catôt của một tế bào quang điện có công thoát là 2,2eV. Chiếu vào catôt bức xạ điện từ có bước sóng \(\lambda \) . Để triệt tiêu dòng quang điện cần đặt một hiệu điện thế hãm Uh = 0,4 V. Tần số của bức xạ điện từ là:
Câu 21 :
Phát biểu nào sau đây không đúng khi nói về hiện tượng quang dẫn
Câu 22 :
Cho h = 6,625.10-34Js, c = 3.108m/s. Tính năng lượng của phôtôn có bước sóng 500nm?
Câu 23 :
Nguyên tắc hoạt động của quang trở dựa vào hiện tượng nào?
Câu 24 :
Công thoát của kim loại làm catốt của một tế bào quang điện là 2,5eV. Khi chiếu bức xạ có bước sóng \(\lambda \) vào catốt thì các electron quang điện bật ra có động năng cực đại là 1,5eV. Bước sóng của bức xạ nói trên là:
Câu 25 :
Cường độ dòng điện bão hòa bằng \(40\mu A\) thì số electron bị bứt ra khỏi catốt tế bào quang điện trong 1 giây là:
Câu 26 :
Chất lỏng fluorexein hấp thụ ánh sáng kích thích có bước sóng λ = 0,48μm và phát ra ánh sáng có bước sóng λ’ = 0,64μm. Biết hiệu suất của sự phát quang này là 90% (hiệu suất của sự phát quang là tỉ số giữa năng lượng của ánh sáng phát quang và năng lượng của ánh sáng kích thích trong một đơn vị thời gian), số phôtôn của ánh sáng kích thích chiếu đến trong 1s là 2012.1010 hạt. Số phôtôn của chùm sáng phát quang phát ra trong 1s là:
Câu 27 :
Nguồn sáng thứ nhất có công suất P1 phát ra ánh sáng đơn sắc có bước sóng \({\lambda _1} = 450nm\). Nguồn sáng thứ hai có công suất P2 phát ra ánh sáng đơn sắc có bước sóng \({\lambda _2} = 0,60\mu m\). Trong cùng một khoảng thời gian, tỉ số giữa số photon mà nguồn thứ nhất phát ra so với số photon mà nguồn thứ hai phát ra là 3:1. Tỉ số P1 và P2 là:
Câu 28 :
Bước sóng dài nhất để bứt được electrôn ra khỏi 2 kim loại a và b lần lượt là \(3nm\) và \(4,5nm\). Công thoát tương ứng là \({A_1}\) và \({A_2}\) sẽ là :
Câu 29 :
Chiếu ánh sáng đơn sắc có bước sóng \(\lambda = {\rm{ }}546{\rm{ }}nm\) vào bề mặt ca tốt của một tế bào quang điện. Giả sử các electron đó được tách ra bằng màn chắn dể lấy một chùm hẹp hướng vào một từ trường đều có \(B{\rm{ }} = {\rm{ }}{10^{ - 4}}T\) , sao cho vec tơ B vuông góc với vân tốc của hạt. Biết quỹ đạo của hạt có bán kính cực đại \(R{\rm{ }} = {\rm{ }}23,32{\rm{ }}mm\) . Tìm độ lớn vận tốc ban đầu cực đại của các electron quang điện.
Câu 30 :
Giới hạn quang điện của kim loại là \({\lambda _0}\). Chiếu vào catôt của tế bào quang điện lần lượt hai bức xạ có bước sóng \({\lambda _1} = \dfrac{{{\lambda _0}}}{2}\) và \({\lambda _2} = \dfrac{{{\lambda _0}}}{3}\). Gọi \({U_1}\) và \({U_2}\) là điện áp hãm tương ứng để triệt tiêu dòng quang điện thì:
Câu 31 :
Chiếu lên bề mặt một tấm kim loại có công thoát electrôn là A = 2,1 eV chùm ánh sáng đơn sắc có bước sóng λ = 0,485μm . Người ta tách ra một chùm hẹp các electrôn quang điện có vận tốc ban đầu cực đại hướng vào một không gian có cả điện trường đều E và từ trường đều B . Ba véc tơ v , E , B vuông góc với nhau từng đôi một. Cho B = 5.10-4 T . Để các electrôn vẫn tiếp tục chuyển động thẳng và đều thì cường độ điện trường E có giá trị nào sau đây?
Câu 32 :
Trong thí nghiệm Young về giao thoa ánh sáng, nguồn S phát ra đồng thời ba bức xạ đơn sắc có bước sóng lần lượt là 0,4µm; 0,5µm và 0,6µm. Trên màn, trong khoảng giữa hai vân sáng liên tiếp cùng màu với vân sáng trung tâm, số vị trí mà ở đó chỉ có một bức xạ cho vân sáng?
Lời giải và đáp án
Câu 1 :
Giới hạn quang điện của Cu là 300 nm. Công thoát của electron khỏi Cu là:
Đáp án : B Phương pháp giải :
Sử dụng công thức tính công thoát: \(A{\rm{ }} = {\rm{ }}\dfrac{{h.c}}{{{\lambda _0}}}\) với \(h = {6,625.10^{ - 34}}\): hằng số Plăng; \({\lambda _0}\): giới hạn quang điện Lời giải chi tiết :
- Ta có: \({\lambda _0} = 300nm = {3.10^{ - 7}}m\) - Áp dụng công thức tính công thoát: \(A{\rm{ }} = {\rm{ }}\dfrac{{h.c}}{{{\lambda _0}}} = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{3.10}^{ - 7}}}} = {6,625.10^{ - 19}}J = \dfrac{{{{6,625.10}^{ - 19}}}}{{{{1,6.10}^{ - 19}}}} = 4,14eV\)
Câu 2 :
Các bức xạ trong dãy Banme thuộc vùng nào trong các vùng sau?
Đáp án : B Phương pháp giải :
Sử dụng lí thuyết về quang phổ của nguyên tử Hidro (dãy Laiman, Banme, Passen) Lời giải chi tiết :
A – sai vì các bức xạ trong dãy Passen mới thuộc vùng hồng ngoại B – đúng vì các bức xạ của dãy Banme một phần nằm trong vùng ánh sáng nhìn thấy,một phần nằm trong vùng tử ngoại C – sai vì các bức xạ trong dãy Lai man mới thuộc vùng tử ngoại D – sai vì các bức xạ của dãy Banme một phần nằm trong vùng ánh sáng nhìn thấy,một phần nằm trong vùng tử ngoại
Câu 3 :
Kim loại dùng làm Catot của một tế bào quang điện có \(A{\rm{ }} = {\rm{ }}6,625{\rm{ }}eV\). Lần lượt chiếu vào catot các bước sóng: \({\lambda _1} = 0,1875\mu m\); \({\lambda _2} = 0,1925\mu m\); \({\lambda _3} = 0,1685\mu m\). Hỏi bước sóng nào gây ra được hiện tượng quang điện?
Đáp án : C Phương pháp giải :
- Sử dụng công thức tính công thoát để tính giới hạn quang điện \({\lambda _0}\):\(A{\rm{ }} = {\rm{ }}\dfrac{{h.c}}{{{\lambda _0}}} \to {\lambda _0} = \dfrac{{h.c}}{A}\) - Điều kiện xảy ra hiện tượng quang điện là: \(\lambda \le {\lambda _0}\)với \({\lambda _0}\): giới hạn quang điện Lời giải chi tiết :
- Ta có: \(A{\rm{ }} = {\rm{ }}\dfrac{{h.c}}{{{\lambda _0}}} \to {\lambda _0} = \dfrac{{h.c}}{A} = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{6,625.1,6.10}^{ - 19}}}} = {0,1875.10^{ - 6}}m = 0,1875\mu m\) - Điều kiện xảy ra hiện tượng quang điện là: \(\lambda \le {\lambda _0} \to \) \({\lambda _1},{\lambda _3}\)gây ra được hiện tượng quang điện
Câu 4 :
Động năng ban đầu cực đại của các e phụ thuộc vào?
Đáp án : D Phương pháp giải :
Sử dụng công thức Anhxtanh: \(\xi = \dfrac{{h.c}}{\lambda } = A + {{\rm{W}}_{od\max }} = \dfrac{{h.c}}{{{\lambda _0}}} + {{\rm{W}}_{od\max }}\) Lời giải chi tiết :
- Sử dụng công thức Anhxtanh: \(\xi = A + {{\rm{W}}_{od\max }} \to {{\rm{W}}_{od\max }} = \xi - A\) \( \to \) Động năng ban đầu cực đại của các e phụ thuộc vào năng lượng của photon chiếu tới và công thoát \( \to \) D đúng
Câu 5 :
Chiếu một chùm bức xạ đơn sắc vào một tấm kẽm có giới hạn quang điện \(0,35μm\) . Hiện tượng quang điện sẽ không xảy ra khi chùm bức xạ có bước sóng là
Đáp án : D Phương pháp giải :
Sử dụng điều kiện xảy ra hiện tượng quang điện là: \(\lambda \le {\lambda _0}\) Lời giải chi tiết :
- Ta có: \({\lambda _0} = 0,35\mu m\) - Sử dụng điều kiện xảy ra hiện tượng quang điện là: \(\lambda \le {\lambda _0}\) \( \to \) hiện tượng quang điện sẽ không xảy ra với bước sóng là \(0,4\mu m\)
Câu 6 :
Theo quan điểm của thuyết lượng tử phát biểu nào sau đây là không đúng?
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết của thuyết lượng tử Ánh sáng: - Chùm ánh sáng là một chùm hạt ( phôtôn ; các lượng tử ánh sáng) - Mỗi phôtôn có năng lượng xác định e = hf (f là tần số của sóng ánh sáng đơn sắc tương ứng); năng lượng của photon ánh sáng không đổi khi ánh sáng truyền đi và không phụ thuộc khoảng cách đến nguồn sáng - Cường độ của chùm sáng tỉ lệ với số phôtôn phát ra trong 1 giây. - Các phôtôn bay dọc theo tia sáng với tốc độ \(c = {3.10^8}m/s\) trong chân không Lời giải chi tiết :
A,B,C – đúng D – sai vì các photn bay dọc theo tia sáng với tốc độ \(c = {3.10^8}m/s\), tuy nhiên các photon tong các chùm sáng khác nhau có bước sóng khác nhau, dẫn tới năng lượng \(\xi = \dfrac{{h.c}}{\lambda }\)là khác nhau
Câu 7 :
Công thoát của kim loại Na là 2,48 eV. Chiếu một chùm bức xạ có bước sóng \(0,36\mu m\) vào tế bào quang điện có catôt làm bằng Na thì cường độ dòng quang điện bão hoà là 3mA . Số êlectron bị bứt ra khỏi catôt trong mỗi giây là:
Đáp án : A Phương pháp giải :
Sử dụng công thức tính \({n_e} = \dfrac{{{I_{bh}}}}{e}\) Lời giải chi tiết :
Ta có: \({n_e} = \dfrac{{{I_{bh}}}}{e} = \dfrac{{{{3.10}^{ - 3}}}}{{{{1,6.10}^{ - 19}}}} = {1,875.10^{16}}\)
Câu 8 :
Phát biểu nào sau đây là ĐÚNG khi nói về quang phổ của nguyên tử H
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết về quang phổ Hidro: quang phổ Hidro là quang phổ vạch phát xạ bao gồm 3 dãy: dãy Laiman (thuộc vùng tử ngoại); dãy Banme (một phần thuộc vùng tử ngoại, một phần thuộc vùng ánh sáng nhìn thấy); dãy Passen (thuộc vùng hồng ngoại) Lời giải chi tiết :
A,B- sai vì quang phổ của nguyên tử H là quang phổ vạch, gồm 4 vạch màu đỏ, lam, chàm, tím C- sai vì giữa các dãy Laiman, Banme, Passen có ranh giới xác định D- đúng
Câu 9 :
Giới hạn quang điện của Na là \(0,50\mu m\). Chiếu vào Na tia tử ngoại có bước sóng \(\lambda = 0,25\mu m\). Vận tốc ban đầu cực đại của electron quang điện là:
Đáp án : B Phương pháp giải :
Sử dụng công thức Anhxtanh: \(\xi = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + \dfrac{1}{2}mv_{\max }^2 \to {v_{\max }}\) Lời giải chi tiết :
\(\lambda = 0,25\mu m = {0,25.10^{ - 6}}m\); \({\lambda _0} = 0,50\mu m = {0,5.10^{ - 6}}m\) Ta có: \(\begin{array}{l}\xi = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + \dfrac{1}{2}mv_{\max }^2\\ \to {v_{\max }} = \sqrt {\dfrac{{2.h.c}}{m}(\dfrac{1}{\lambda } - \dfrac{1}{{{\lambda _0}}})} = \sqrt {\dfrac{{{{2.6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{9,1.10}^{ - 31}}}}(\dfrac{1}{{{{0,25.10}^{ - 6}}}} - \dfrac{1}{{{{0,5.10}^{ - 6}}}})} = {9,34.10^5}m/s\end{array}\)
Câu 10 :
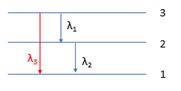
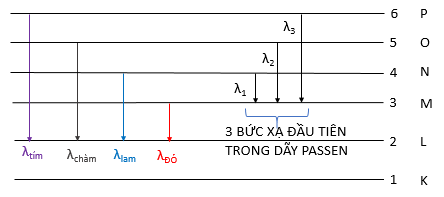
Gọi \({\lambda _\alpha }\) và \({\lambda _\beta }\) lần lượt là 2 bước sóng của 2 vạch \(H{_\alpha }\) và \({H_\beta }\) trong dãy Banme. Gọi \({\lambda _1}\) là bước sóng của vạch đầu tiên trong dãy Pasen. Xác định mối liên hệ của \({\lambda _\alpha },{\lambda _\beta },{\lambda _1}\)
Đáp án : C Phương pháp giải :
Sử dụng công thức: \(\dfrac{1}{{{\lambda _3}}} = \dfrac{1}{{{\lambda _1}}} + \dfrac{1}{{{\lambda _2}}}\)
Lời giải chi tiết :
Thay \({\lambda _\alpha } = {\lambda _{do}};{\lambda _\beta } = {\lambda _{lam}} \to \dfrac{1}{{{\lambda _1}}} = \dfrac{1}{{{\lambda _\beta }}} - \dfrac{1}{{{\lambda _\alpha }}}\)
Câu 11 :
Chiếu ánh sáng đơn sắc có bước sóng \(320{\rm{ }}nm\) vào bề mặt ca tốt của một tế bào quang điện làm bằng xedi có giới hạn quang điện là \({\lambda _0} = 660nm\). Hiệu điện thế hãm của nó có giá trị là:
Đáp án : C Phương pháp giải :
Sử dụng công thức Anhxtanh: \({\rm{\xi = A + e}}{\rm{.}}{{\rm{U}}_h} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _o}}} + e.{U_h} \to {U_h} = \dfrac{{h.c}}{e}(\dfrac{1}{\lambda } - \dfrac{1}{{{\lambda _0}}})\) Lời giải chi tiết :
Ta có: \({\rm{\xi = A + e}}{\rm{.}}{{\rm{U}}_h} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _o}}} + e.{U_h} \to {U_h} = \dfrac{{h.c}}{e}(\dfrac{1}{\lambda } - \dfrac{1}{{{\lambda _0}}}) = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{1,6.10}^{ - 19}}}}(\dfrac{1}{{{{320.10}^{ - 9}}}} - \dfrac{1}{{{{660.10}^{ - 9}}}}) = 2V\)
Câu 12 :
Dãy Laiman trong quang phổ vạch của Hiđrô ứng với sự dịch chuyển của các electron từ các quỹ đạo dừng có năng lượng cao về quỹ đạo:
Đáp án : A Phương pháp giải :
Sử dụng lí thuyết về các dãy Laiman, Banme, Passen trong quang phổ vạch của Hidro Lời giải chi tiết :
Ta có: Dãy Laiman trong quang phổ vạch của Hiđrô ứng với sự dịch chuyển của các electron từ các quỹ đạo dừng có năng lượng cao về quỹ đạo K
Câu 13 :
Trong một tế bào quang điện có \({I_{bh}} = 2\mu A\) và hiệu suất lượng tử là \(0,5\% \). Số photon đến Ca tốt mỗi giây là:
Đáp án : C Phương pháp giải :
- Sử dụng công thức tính hiệu suất lượng tử: \(H = \dfrac{{{n_e}}}{{{N_f}}}.100\% \) - Công thức tính số e thoát ra khỏi anot: \({n_e} = \dfrac{{{I_{bh}}}}{e}\) - Công thức tính số photon đập vào catot: \({n_f} = \dfrac{P}{\xi } = \dfrac{P}{{\dfrac{{hc}}{\lambda }}}\) Lời giải chi tiết :
- Ta có: \({n_e} = \dfrac{{{I_{bh}}}}{e} = \dfrac{{{{2.10}^{ - 6}}}}{{{{1,6.10}^{ - 19}}}} = {1,25.10^{13}}\) - Lại có: \(H = \dfrac{{{n_e}}}{{{N_f}}}.100\% \to {N_f} = \dfrac{{{{1,25.10}^{13}}.100\% }}{{0,5}} = {2,5.10^{15}}\)
Câu 14 :
Chiếu một bức xạ có bước sóng λ = 0, 48µm lên một tấm kim loại có công thoát A = 2,4.10-19J. dùng màn chắn tách ra một chùm hẹp các êlectron quang điện và hướng chúng bay theo chiều véc tơ cường độ điện trường có E = 1000 V/m. Quãng đường tối đa mà êlectron chuyển động được theo chiều véc tơ cường độ điện trường xấp xỉ là:
Đáp án : D Phương pháp giải :
Áp dụng công thức Anh – xtanh và lí thuyết về chuyển động thẳng biến đổi đều Công thức Anh – xtanh: \({{hc} \over \lambda } = A + {1 \over 2}mv_0^2\) Lực điện: F = qE Công thức của chuyển động thẳng biến đổi đều: \({v^2} - v_0^2 = 2as\) Lời giải chi tiết :
+ Theo công thức Anh - xtanh : \({{hc} \over \lambda } = A + {1 \over 2}m.{v_0}^2 \Rightarrow {v_0}^2 = {2 \over m}\left( {{{hc} \over \lambda } - A} \right)\) \(({m_e} = {9,1.10^{ - 31}}kg)\) + Ta có: \(a = {F \over m} = {{qE} \over m}\) + Chuyển động của e là chuyển động chậm dần đều với vận tốc đầu v0 và gia tốc a Electron dừng => v = 0 \( \Leftrightarrow {0^2}-{\rm{ }}{v_0}^2 = {\rm{ }}2as \Rightarrow s = - {{{v_0}^2} \over {2a}} = - {{{2 \over m}\left( {{{hc} \over \lambda } - A} \right)} \over {2.{{qE} \over m}}} = - {{{{hc} \over \lambda } - A} \over {qE}} \Rightarrow s = 0,109cm\)
Câu 15 :
Cho giới hạn quang điện của catot là \({\lambda _0} = 660nm\) và đặt vào đó giữa Anot và Catot một \({U_{AK}} = {\rm{ }}1,5{\rm{ }}V\). Dùng bức xạ có \(\lambda = 330nm\). Động năng cực đại của các quang electron khi đập vào anot là:
Đáp án : D Phương pháp giải :
- Sử dụng công thức Anhxtanh \(\xi = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + {{\rm{W}}_{od\max }}\) - Sử dụng định lí biến thiên động năng: \({{\rm{W}}_{od\max }} - {{\rm{W}}_{dm{\rm{ax}}}} = e.{U_{AK}} \to {{\rm{W}}_{dm{\rm{ax}}}} = {{\rm{W}}_{od\max }} - e.{U_{AK}}\) Lời giải chi tiết :
- Ta có, \(\begin{array}{l}\xi = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + {{\rm{W}}_{od\max }}\\ \to {{\rm{W}}_{od\max }} = h.c.(\dfrac{1}{\lambda } - \dfrac{1}{{{\lambda _0}}}) = {6,625.10^{ - 34}}{.3.10^8}.(\dfrac{1}{{{{0,33.10}^{ - 6}}}} - \dfrac{1}{{{{0,66.10}^{ - 6}}}}) = {3,01.10^{ - 19}}J\end{array}\) - Sử dụng định lí biến thiên động năng: \(\begin{array}{l}{{\rm{W}}_{dm{\rm{ax}}}} - {{\rm{W}}_{od\max }} = e.{U_{AK}}\\ \to {{\rm{W}}_{dm{\rm{ax}}}} = {{\rm{W}}_{od\max }} + e.{U_{AK}} = {3,01.10^{ - 19}} + {1,6.10^{ - 19}}.1,5 = {5,41.10^{ - 19}}J\end{array}\)
Câu 16 :
Chiếu ánh sáng đơn sắc có bước sóng \(\lambda = 330nm\) vào bề mặt ca tốt của một tế bào quang điện hiệu điện thế hãm của nó có giá trị là \({U_h}\). Cho giới hạn quang điện của catot là \({\lambda _0} = 660nm\) và đặt vào đó giữa Anot và Catot một \({U_{AK}} = {\rm{ }}1,5{\rm{ }}V\). Tính động năng cực đại của các quang electron khi đập vào anot nếu dùng bức xạ \(\lambda ' = 282,5nm\):
Đáp án : B Phương pháp giải :
- Sử dụng công thức Anhxtanh \(\xi = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + {{\rm{W}}_{od\max }}\) - Sử dụng định lí biến thiên động năng: \({{\rm{W}}_{od\max }} - {{\rm{W}}_{dm{\rm{ax}}}} = e.{U_{AK}} \to {{\rm{W}}_{dm{\rm{ax}}}} = {{\rm{W}}_{od\max }} - e.{U_{AK}}\) Lời giải chi tiết :
- Ta có, \(\begin{array}{l}\xi = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + {{\rm{W}}_{od\max }}\\ \to {{\rm{W}}_{od\max }} = h.c.(\dfrac{1}{\lambda } - \dfrac{1}{{{\lambda _0}}}) = {6,625.10^{ - 34}}{.3.10^8}.(\dfrac{1}{{{{0,2825.10}^{ - 6}}}} - \dfrac{1}{{{{0,66.10}^{ - 6}}}}) = {4,02.10^{ - 19}}J\end{array}\) - Sử dụng định lí biến thiên động năng: \(\begin{array}{l}{{\rm{W}}_{dm{\rm{ax}}}} - {{\rm{W}}_{od\max }} = e.{U_{AK}}\\ \to {{\rm{W}}_{dm{\rm{ax}}}} = {{\rm{W}}_{od\max }} + e.{U_{AK}} = {4,02.10^{ - 19}} + {1,6.10^{ - 19}}.1,5 = {6,42.10^{ - 19}}J\end{array}\)
Câu 17 :
Chiếu ánh sáng đơn sắc có bước sóng \(\lambda = 546{\rm{ }}nm\) vào bề mặt ca tốt của một tế bào quang điện, có \({I_{bh}} = {\rm{ }}2{\rm{ }}mA\). Công suất lượng tử là \(P{\rm{ }} = {\rm{ }}1,515{\rm{ }}W\). Tính hiệu suất lượng tử.
Đáp án : A Phương pháp giải :
- Sử dụng công thức tính hiệu suất lượng tử: \(H = \dfrac{{{n_e}}}{{{N_f}}}.100\% \) - Công thức tính số e thoát ra khỏi anot: \({n_e} = \dfrac{{{I_{bh}}}}{e}\) - Công thức tính số photon đập vào catot: \({n_f} = \dfrac{P}{\xi } = \dfrac{P}{{\dfrac{{hc}}{\lambda }}}\) Lời giải chi tiết :
- Ta có: \({n_e} = \dfrac{{{I_{bh}}}}{e} = \dfrac{{{{2.10}^{ - 3}}}}{{{{1,6.10}^{ - 19}}}} = {1,25.10^{16}}\) \({n_f} = \dfrac{P}{\xi } = \dfrac{P}{{\dfrac{{hc}}{\lambda }}} = \dfrac{{1,515}}{{\dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{546.10}^{ - 9}}}}}} = {4,16.10^{18}}\) \( \to H = \dfrac{{{n_e}}}{{{N_f}}}.100\% = \dfrac{{{{1,25.10}^{16}}}}{{{{4,16.10}^{18}}}} = {30.10^{ - 2}}\% \)
Câu 18 :
Năng lượng cần thiết để iôn hoá nguyên tử kim loại là 2,2eV. Kim loại này có giới hạn quang điện là:
Đáp án : B Phương pháp giải :
Sử dụng khái niệm năng lượng cần thiết để ion hóa nguyên tử là năng lượng cần cung cấp để đưa electron từ trạng thái cơ bản ra xa vô cực: \(\Delta {\rm{W = }}\dfrac{{hc}}{{{\lambda _0}}}\) Lời giải chi tiết :
Ta có: \(\Delta {\rm{W = }}\dfrac{{hc}}{{{\lambda _0}}} \to {\lambda _0} = \dfrac{{hc}}{{\Delta {\rm{W}}}} = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{2,2.1,6.10}^{ - 19}}}} = {5,6.10^{ - 7}}m = 0,56\mu m\)
Câu 19 :
Chiếu đồng thời hai bức xạ vào một tế bào quang điện, ta cần dùng các hiệu điện thế hãm để triệt tiêu dòng quang điện. Cho biết Uh1= 2Uh2. Hỏi có thể kết luận gì?
Đáp án : B Phương pháp giải :
Sử dụng công thức: \(\xi = A + e.{U_h}\); \(\xi = \dfrac{{h.c}}{\lambda }\) Lời giải chi tiết :
Ta có: \(\begin{array}{l}\xi = A + e.{U_h}\\ \to {\xi _1} = A + e.{U_{h1}};{\xi _2} = A + e.{U_{h2}}\end{array}\) Vì \({U_{h1}} = 2{U_{h2}} \to {\xi _1} > {\xi _2}\) Lại có: \(\xi = \dfrac{{h.c}}{\lambda }\) \( \to {\lambda _1} < {\lambda _2}\)
Câu 20 :
Kim loại dùng làm catôt của một tế bào quang điện có công thoát là 2,2eV. Chiếu vào catôt bức xạ điện từ có bước sóng \(\lambda \) . Để triệt tiêu dòng quang điện cần đặt một hiệu điện thế hãm Uh = 0,4 V. Tần số của bức xạ điện từ là:
Đáp án : D Phương pháp giải :
Sử dụng công thức:\(\xi = A + e.{U_h} \to h.f = A + e.{U_h}\) Lời giải chi tiết :
Ta có: \(\xi = A + e.{U_h} \to h.f = A + e.{U_h} \to f = \dfrac{{A + e.{U_h}}}{h} = \dfrac{{{{2,2.1,6.10}^{ - 19}} + {{1,6.10}^{ - 19}}.0,4}}{{{{6,625.10}^{ - 34}}}} = {6,28.10^{14}}(Hz)\)
Câu 21 :
Phát biểu nào sau đây không đúng khi nói về hiện tượng quang dẫn
Đáp án : B Phương pháp giải :
- Sử dụng lí thuyết về hiện tượng quang dẫn: Hiện tượng quang dẫn là hiện tượng khi chiếu ánh sáng thích hợp vào một khối bán dẫn, electron liên kết được giải phóng tạo thành electron dẫn - Điều kiện xảy ra hiện tượng quang dẫn là: \(\lambda \le {\lambda _0}\)với \({\lambda _0}\): giới hạn quang dẫn Lời giải chi tiết :
A,C- đúng vì Hiện tượng quang dẫn là hiện tượng khi chiếu ánh sáng thích hợp vào một khối bán dẫn, electron liên kết được giải phóng tạo thành electron dẫn B- sai vì giới hạn quang dẫn \({\lambda _0}\)là bước sóng kích thích dài nhất mà còn có thể gây ra hiện tượng quang dẫn D- đúng vì ánh sáng kích thích của hiện tượng quang dẫn không cần phải có năng lượng lớn
Câu 22 :
Cho h = 6,625.10-34Js, c = 3.108m/s. Tính năng lượng của phôtôn có bước sóng 500nm?
Đáp án : C Phương pháp giải :
Sử dụng công thức: \(\xi = h.f = \dfrac{{h.c}}{\lambda }\) Lời giải chi tiết :
Ta có: \(\xi = h.f = \dfrac{{h.c}}{\lambda } = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{500.10}^{ - 9}}}} = {3,975.10^{ - 19}}J = 2,5eV\)
Câu 23 :
Nguyên tắc hoạt động của quang trở dựa vào hiện tượng nào?
Đáp án : A Lời giải chi tiết :
B, C, D- sai vì quang điện trở hoạt động dựa trên hiện tượng quang điện trong
Câu 24 :
Công thoát của kim loại làm catốt của một tế bào quang điện là 2,5eV. Khi chiếu bức xạ có bước sóng \(\lambda \) vào catốt thì các electron quang điện bật ra có động năng cực đại là 1,5eV. Bước sóng của bức xạ nói trên là:
Đáp án : A Phương pháp giải :
Sử dụng công thức Anhxtanh:\(\xi = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = A + {{\rm{W}}_{od\max }}\) Lời giải chi tiết :
Ta có: \(\xi = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = A + {{\rm{W}}_{od\max }} \to \lambda = \dfrac{{h.c}}{{A + {{\rm{W}}_{od\max }}}} = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{(2,5 + 1,5){{.1,6.10}^{ - 19}}}} = {3,1.10^{ - 7}}m = 0,31\mu m\)
Câu 25 :
Cường độ dòng điện bão hòa bằng \(40\mu A\) thì số electron bị bứt ra khỏi catốt tế bào quang điện trong 1 giây là:
Đáp án : A Phương pháp giải :
Sử dụng công thức \({n_e} = \dfrac{{{I_{bh}}}}{e}\) Lời giải chi tiết :
Ta có: \({n_e} = \dfrac{{{I_{bh}}}}{e} = \dfrac{{{{40.10}^{ - 6}}}}{{{{1,6.10}^{ - 19}}}} = {2,5.10^{14}}Hz\)
Câu 26 :
Chất lỏng fluorexein hấp thụ ánh sáng kích thích có bước sóng λ = 0,48μm và phát ra ánh sáng có bước sóng λ’ = 0,64μm. Biết hiệu suất của sự phát quang này là 90% (hiệu suất của sự phát quang là tỉ số giữa năng lượng của ánh sáng phát quang và năng lượng của ánh sáng kích thích trong một đơn vị thời gian), số phôtôn của ánh sáng kích thích chiếu đến trong 1s là 2012.1010 hạt. Số phôtôn của chùm sáng phát quang phát ra trong 1s là:
Đáp án : B Phương pháp giải :
- Sử dụng công thức tính năng lượng của một photon: \(\xi = \dfrac{{h.c}}{\lambda }\) - Công thức tính năng lượng của N photon: \(E = N.\xi = N.\dfrac{{h.c}}{\lambda }\) - Hiệu suất của sự phát quang: \(H = \dfrac{{{E_2}}}{{{E_1}}}.100\% \); Trong đó: \({E_2}\): năng lượng của ánh sáng phát quang; \({E_1}\): năng lượng của ánh sáng kích thích (trong cùng một đơn vị thời gian) Lời giải chi tiết :
Ta có: - Năng lượng của ánh sáng kích thích đến trong 1 s là: \({E_1} = {N_1}.{\xi _1} = {N_1}.\dfrac{{h.c}}{{{\lambda _1}}}\) - Năng lượng của ánh sáng phát ra trong 1 s là: \({E_2} = {N_2}.{\xi _2} = {N_2}.\dfrac{{h.c}}{{{\lambda _2}}}\) - Ta lại có: hiệu suất của sự phát quang: \(H = \dfrac{{{E_2}}}{{{E_1}}}.100\% = \dfrac{{{N_2}.{\lambda _1}}}{{{N_1}.{\lambda _2}}}.100\% \to {N_2} = \dfrac{{H.{N_1}.{\lambda _2}}}{{{\lambda _1}.100\% }} = \dfrac{{{{90.2012.10}^{10}}{{.0,64.10}^{ - 6}}}}{{{{0,48.10}^{ - 6}}.100\% }} = {2,4144.10^{13}}\)(hạt)
Câu 27 :
Nguồn sáng thứ nhất có công suất P1 phát ra ánh sáng đơn sắc có bước sóng \({\lambda _1} = 450nm\). Nguồn sáng thứ hai có công suất P2 phát ra ánh sáng đơn sắc có bước sóng \({\lambda _2} = 0,60\mu m\). Trong cùng một khoảng thời gian, tỉ số giữa số photon mà nguồn thứ nhất phát ra so với số photon mà nguồn thứ hai phát ra là 3:1. Tỉ số P1 và P2 là:
Đáp án : A Phương pháp giải :
Sử dụng công thức tính số photon đập vào catot: \({n_f} = \dfrac{P}{\xi } = \dfrac{P}{{\dfrac{{hc}}{\lambda }}}\) Lời giải chi tiết :
Ta có: \({n_f} = \dfrac{P}{\xi } = \dfrac{P}{{\dfrac{{hc}}{\lambda }}} \to \dfrac{{{n_{f1}}}}{{{n_{f2}}}} = \dfrac{{{P_1}.{\lambda _1}}}{{{P_2}.{\lambda _2}}} \to \dfrac{3}{1} = \dfrac{{{P_1}.450}}{{{P_2}.600}} \to \dfrac{{{P_1}}}{{{P_2}}} = 4\)
Câu 28 :
Bước sóng dài nhất để bứt được electrôn ra khỏi 2 kim loại a và b lần lượt là \(3nm\) và \(4,5nm\). Công thoát tương ứng là \({A_1}\) và \({A_2}\) sẽ là :
Đáp án : B Phương pháp giải :
Sử dụng công thức tính công thoát: \(A = \dfrac{{h.c}}{{{\lambda _0}}}\) Lời giải chi tiết :
Ta có: \({A_1} = \dfrac{{h.c}}{{{\lambda _{01}}}};{A_2} = \dfrac{{h.c}}{{{\lambda _{02}}}} \to \dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{{\lambda _{02}}}}{{{\lambda _{01}}}} = \dfrac{{4,5}}{3} = 1,5 \to {A_1} = 1,5{A_2}\)
Câu 29 :
Chiếu ánh sáng đơn sắc có bước sóng \(\lambda = {\rm{ }}546{\rm{ }}nm\) vào bề mặt ca tốt của một tế bào quang điện. Giả sử các electron đó được tách ra bằng màn chắn dể lấy một chùm hẹp hướng vào một từ trường đều có \(B{\rm{ }} = {\rm{ }}{10^{ - 4}}T\) , sao cho vec tơ B vuông góc với vân tốc của hạt. Biết quỹ đạo của hạt có bán kính cực đại \(R{\rm{ }} = {\rm{ }}23,32{\rm{ }}mm\) . Tìm độ lớn vận tốc ban đầu cực đại của các electron quang điện.
Đáp án : D Phương pháp giải :
Sử dụng công thức tính bán kính quĩ đạo của electron chuyển động vuông góc với từ trường: \({R_{{\rm{max}}}} = \dfrac{{m.{v_{{\rm{max}}}}}}{{q.B}}\) Lời giải chi tiết :
Ta có: \({R_{{\rm{max}}}} = \dfrac{{m.{v_{{\rm{max}}}}}}{{q.B}} \to {v_{{\rm{max}}}} = \dfrac{{{R_{{\rm{max}}}}q.B}}{m} = \dfrac{{{{23,32.10}^{ - 3}}{{.1,6.10}^{ - 19}}{{.10}^{ - 4}}}}{{{{9,1.10}^{ - 31}}}} = {4,1.10^5}(m/s)\)
Câu 30 :
Giới hạn quang điện của kim loại là \({\lambda _0}\). Chiếu vào catôt của tế bào quang điện lần lượt hai bức xạ có bước sóng \({\lambda _1} = \dfrac{{{\lambda _0}}}{2}\) và \({\lambda _2} = \dfrac{{{\lambda _0}}}{3}\). Gọi \({U_1}\) và \({U_2}\) là điện áp hãm tương ứng để triệt tiêu dòng quang điện thì:
Đáp án : C Phương pháp giải :
Sử dụng công thức Anhxtanh: \(\xi = A + e.{U_h} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + e.{U_h}\) Lời giải chi tiết :
Ta có: \(\dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + e.{U_h}\) \(\begin{array}{l} \to \dfrac{{h.c}}{{{\lambda _1}}} = \dfrac{{h.c}}{{{\lambda _0}}} + e.{U_{h1}};\dfrac{{h.c}}{{{\lambda _2}}} = \dfrac{{h.c}}{{{\lambda _0}}} + e.{U_{h2}}\\ \to \dfrac{{h.c}}{{{\lambda _0}/2}} = \dfrac{{h.c}}{{{\lambda _0}}} + e.{U_1};\dfrac{{h.c}}{{{\lambda _0}/3}} = \dfrac{{h.c}}{{{\lambda _0}}} + e.{U_2}\\ \to \dfrac{{2h.c}}{{{\lambda _0}}} = \dfrac{{h.c}}{{{\lambda _0}}} + e.{U_1};\dfrac{{3h.c}}{{{\lambda _0}}} = \dfrac{{h.c}}{{{\lambda _0}}} + e.{U_2}\\ \to e.{U_1} = \dfrac{{h.c}}{{{\lambda _0}}};e.{U_2} = \dfrac{{2h.c}}{{{\lambda _0}}}\\ \to {U_1} = 0,5{U_2}\end{array}\)
Câu 31 :
Chiếu lên bề mặt một tấm kim loại có công thoát electrôn là A = 2,1 eV chùm ánh sáng đơn sắc có bước sóng λ = 0,485μm . Người ta tách ra một chùm hẹp các electrôn quang điện có vận tốc ban đầu cực đại hướng vào một không gian có cả điện trường đều E và từ trường đều B . Ba véc tơ v , E , B vuông góc với nhau từng đôi một. Cho B = 5.10-4 T . Để các electrôn vẫn tiếp tục chuyển động thẳng và đều thì cường độ điện trường E có giá trị nào sau đây?
Đáp án : A Phương pháp giải :
- Sử dụng công thức \(\dfrac{{h.c}}{\lambda } = A + \dfrac{1}{2}m{v^2}_{{\rm{max}}}\)để tính \({v_{{\rm{max}}}}\) - Sử dụng công thức tính lực điện: \(F = qE\) - Sử dụng công thức tính lực Lo ren xơ: \({F_L} = qvB\) - Electron chuyển động thẳng đều trong vùng không gian có cả từ trường đều và điện trường đều: \(F = {F_L} \to qE = qvB \to E = vB\) Lời giải chi tiết :
- Ta có: \(\dfrac{{h.c}}{\lambda } = A + \dfrac{1}{2}m{v^2}_{{\rm{max}}} \to {v_{{\rm{max}}}} = \sqrt {\dfrac{2}{m}(\dfrac{{h.c}}{\lambda } - A)} = \sqrt {\dfrac{2}{{{{9,1.10}^{ - 31}}}}(\dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{0,485.10}^{ - 6}}}} - {{2,1.1,6.10}^{ - 19}})} = {4,03.10^5}(m/s)\) - Electron chuyển động thẳng đều trong vùng không gian có cả từ trường đều và điện trường đều khi lực điện cân bằng với lực Lo ren xo: \(F = {F_L} \to qE = qvB \to E = vB = {4,03.10^5}{.5.10^{ - 4}} = 201,4(V/m)\)
Câu 32 :
Trong thí nghiệm Young về giao thoa ánh sáng, nguồn S phát ra đồng thời ba bức xạ đơn sắc có bước sóng lần lượt là 0,4µm; 0,5µm và 0,6µm. Trên màn, trong khoảng giữa hai vân sáng liên tiếp cùng màu với vân sáng trung tâm, số vị trí mà ở đó chỉ có một bức xạ cho vân sáng?
Đáp án : B Phương pháp giải :
Khoảng vân: \(i = \frac{{\lambda D}}{a}\) Vì ba ánh sáng cùng cho các vân sáng, nên vị trí ba vân sáng trùng nhau thỏa mãn : \(x = {k_1}.\frac{{{\lambda _1}.D}}{a} = {k_2}.\frac{{{\lambda _2}.D}}{a} = {k_3}.\frac{{{\lambda _3}.D}}{a} \Rightarrow {i_1}:{i_2}:{i_3} = {\lambda _1}:{\lambda _2}:{\lambda _3} = a:b:c\) Khi xác định vị trí vân sáng của một ánh sáng đơn sắc, ta tìm số vân trong khoảng giữa hai vân sáng trùng 3 màu trừ đi số vân sáng trùng hai màu từng cặp. Lời giải chi tiết :
Áp dụng công thức tính khoảng vân \(i = \frac{{\lambda D}}{a}\) Vì ba ánh sáng cùng cho các vân sáng, nên vị trí ba vân sáng trùng nhau thỏa mãn : \(\begin{array}{l} Ta xét vân trung tâm và vân trùng 3 màu đầu tiên, ứng với vị trí: \(x = 15{i_1} = 12{i_2} = 10{i_3}\) Vị trí trùng nhau của hai bước sóng λ1 và λ2 có khoảng vân trùng cặp 12 là: \({i_{12}} = 5{i_1} = 4{i_2}\) Vậy trong khoảng từ vân trung tâm đến vân trùng 3 màu đầu tiên có số vị trí trùng nhau của hai bước sóng λ1 và λ2là: \(\;\left( {15\;:5} \right) - 1 = 2\) Vị trí trùng nhau của hai bước sóng λ1 và λ3 có khoảng vân trùng cặp 13 là: \(\;{i_{13}} = 3{i_1} = 2{i_3}\) Vậy trong khoảng từ vân trung tâm đến vân trùng 3 màu đầu tiên có số vị trí trùng nhau của hai bước sóng λ1 và λ3 là: \(\left( {15\;:3} \right) - 1 = 4\) Vị trí trùng nhau của hai bước sóng λ2 và λ3 có khoảng vân trùng cặp 23 là: \({i_{23}} = 6{i_2} = 5{i_3}\) Vậy trong khoảng từ vân trung tâm đến vân trùng 3 màu đầu tiên có số vị trí trùng nhau của hai bước sóng λ2 và λ3là: \(\left( {12\;:6} \right) - 1 = 1\) Vậy số vị trí chỉ có 1 vạch màu đơn sắc là : \((15 + 12 + 10) - (1.3 + 2.2 + 2.4 + 2.1) = 20\)
|



















Danh sách bình luận