Trắc nghiệm Bài 20. Phương trình dao động mạch LC (q - u - i) - Vật Lí 12Đề bài
Câu 1 :
Phương trình dao động của điện tích trong mạch dao động LC là \(q = {Q_0}\cos (\omega t + \varphi )\). Biểu thức của dòng điện trong mạch là:
Câu 2 :
Phương trình dao động của điện tích trong mạch dao động LC là \(q = {Q_0}\cos (\omega t + \varphi )\). Biểu thức của hiệu điện thế trong mạch là:
Câu 3 :
Biểu thức của cường độ dòng điện trong mạch dao động LC là \(i = {I_0}\cos (\omega t + \varphi )\). Biểu thức của điện tích trong mạch là:
Câu 4 :
Một mạch dao động gồm một tụ điện có điện dung \(C = 10 pF\) và cuộn dây thuần cảm có độ tự cảm \(L = 0,25 mH\), cường độ dòng điện cực đại là \(50 mA\). Tại thời điểm ban đầu cường độ dòng điện qua mạch bằng không. Biểu thức của điện tích trên tụ là:
Câu 5 :
Cho mạch dao động điện từ tự do gồm tụ điện có điện dung C = 1μF. Biết biểu thức cường độ dòng điện trong mạch là i = 20cos(1000t + π/2) mA. Biểu thức điện áp giữa hai bản tụ điện có dạng:
Câu 6 :
Một mạch dao động LC có điện áp 2 bản tụ là u = 5cos(104t) V, điện dung C = 0,4 μF. Biểu thức cường độ dòng điện trong mạch là :
Câu 7 :
Mạch dao động gồm tụ điện có điện dung \(C = 10nF\)và cuộn dây thuần cảm có hệ số tử cảm \(L = {10_{}}mH\). Tụ điện được tích điện đến hiệu điện thế 12V. Sau đó cho tụ phóng điện trong mạch. Lấy \({\pi ^2} = 10\) và gốc thời gian là lúc tụ bắt đầu phóng điện. Biểu thức của dòng điện trong cuộn cảm là :
Câu 8 :
Mạch dao động LC gồm cuộn dây thuần cảm có độ tự cảm \(L = 2mH\) và tụ điện có điện dung \(C = 5pF\) Tụ được tích điện đến hiệu điện thế 10V, sau đó người ta để cho tụ phóng điện trong mạch. Nếu chọn gốc thời gian là lúc tụ bắt đầu phóng điện thì biểu thức của điện tích trên bản tụ điện là:
Câu 9 :
Cho mạch điện như hình vẽ. Biết $C = 500 pF$, $L = 0,2mH$, $E = 1,5 V$. Lấy $π^2= 10$. Tại thời điểm $t = 0$, khóa K chuyển từ 1 sang 2. Thiết lập phương trình biểu diễn sự phụ thuộc của điện tích trên tụ điện C theo thời gian? 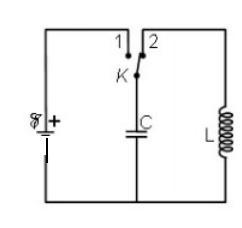
Câu 10 :
Một mạch dao động lí tưởng đang có dao động điện từ tự do với chu kì dao động T. Tại thời điểm t = 0, điện tích trên một bản tụ điện đạt giá trị cực đại. Điện tích trên bản tụ này bằng 0 ở thời điểm đầu tiên (kể từ t = 0) là:
Câu 11 :
Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm 1 H và tụ điện có điện dung 10 μF. Lấy π2 = 10. Lúc đầu, điện tích trên một bản tụ điện đạt giá trị cực đại. Điện tích trên tụ điện có giá trị bằng một nửa giá trị ban đầu sau khoảng thời gian ngắn nhất là:
Câu 12 :
Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm 5μH và tụ điện có điện dung 5 μF. Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là
Câu 13 :
Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Tại thời điểm t = 0, điện tích trên một bản tụ điện cực đại. Sau khoảng thời gian ngắn nhất Δt thì điện tích trên bản tụ này bằng một nửa giá trị cực đại. Chu kì dao động riêng của mạch dao động này là:
Câu 14 :
Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại trên một bản tụ điện là \(4\sqrt 2 \mu C\) và cường độ dòng điện cực đại trong mạch là \(0,5\sqrt 2 \pi A\) Thời gian ngắn nhất để điện tích trên một bản tụ giảm từ q0 đến \(\frac{{{q_0}}}{{\sqrt 2 }}\) là:
Câu 15 :
Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do, thời điểm ban đầu điện tích trên tụ điện đạt giá trị cực đại q0 = 10-8 C. Thời gian ngắn nhất để tụ phóng hết điện tích là 2 μs. Cường độ hiệu dụng của dòng điện trong mạch là:
Câu 16 :
Một mạch dao động điện từ LC lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại trên một bản tụ điện là q0 = 1μC và cường độ dòng điện cực đại trong mạch là I0 = 3π mA. Tính từ thời điểm điện tích trên tụ là q0 , khoảng thời gian ngắn nhất để dòng điện trong mạch có độ lớn bằng I0 là:
Câu 17 :
Khi điện tích trên tụ tăng từ $0$ lên $0,5{\rm{ }}\left( {\mu C} \right)$ thì đồng thời cường độ dòng điện trong mạch dao động LC lí tưởng giảm từ $3\pi \left( {mA} \right)$ xuống \(\dfrac{{3\sqrt 3 \pi }}{2}mA\) . Khoảng thời gian xảy ra sự biến thiên này là:
Câu 18 :
Trong mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Biết thời gian để cường độ dòng điện trong mạch giảm từ giá trị cực đại I0 = 2,22 A xuống còn một nửa là τ = 8/3 (μs). Ở những thời điểm cường độ dòng điện trong mạch bằng không thì điện tích trên tụ bằng:
Câu 19 :
Trong mạch dao động lí tưởng đang có dao động điện từ tự do với chu kỳ T. Biết tụ điện có điện dung \(2nF\) và cuộn cảm có độ tự cảm \(8mH\). Tại thời điểm t1, cường độ dòng điện trong mạch có độ lớn \(5 mA\). Tại thời điểm t2 = t1 + 2π.10-6(s) điện áp giữa hai bản tụ có độ lớn
Câu 20 :
Một mạch dao động lí tưởng gồm cuộn cảm thuần có độ tư cảm \(L\) và tụ điện có điện dung \(C\) đang có dao động điện từ tự do. Ở thời điểm \(t\), dòng điện qua cuộn dây có cường độ bằng \(0\) thì ở thời điểm \(t + \dfrac{{\pi \sqrt {LC} }}{2}\)
Câu 21 :
Một mạch dao động LC lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C đang có dao động điện từ tự do. Điện tích trên một bản tụ ở thời điểm t có dạng biểu thức \(q = {q_0}cos\left( {\omega t + \frac{\pi }{2}} \right)\left( C \right)\) (t tính bằng giây). Kể từ thời điểm ban đầu \(t = 0\), sau khoảng thời gian ngắn nhất \({10^{ - 6}}s\) thì điện tích trên bản tụ bằng 0. Tần số dao động của mạch này là
Câu 22 :
Cường độ dòng điện tức thời trong một mạch dao động là \(i = 0,05\cos 100\pi t\) (A). Hệ số tự cảm của cuộn dây là 2mH. Lấy \({\pi ^2} = 10\). Điện dung và biểu thức điện tích của tụ điện có giá trị nào sau đây?
Câu 23 :
Trong mạch dao động LC lý tưởng, đại lượng nào không thỏa mãn phương trình vi phân dạng \(x'' - {\omega ^2}x = 0\), với \(\omega = \dfrac{1}{{\sqrt {LC} }}\).
Câu 24 :
Một mạch dao động LC lí tưởng với \(q\) là điện tích trên tụ, \(i\) là dòng điện tức thời trong mạch. Đồ thị thể hiện sự phụ thuộc của \({q^2}\) vào \({i^2}\) như hình vẽ. Bước sóng mà mạch thu được trong không khí là
Lời giải và đáp án
Câu 1 :
Phương trình dao động của điện tích trong mạch dao động LC là \(q = {Q_0}\cos (\omega t + \varphi )\). Biểu thức của dòng điện trong mạch là:
Đáp án : B Phương pháp giải :
Xem lí thuyết mục 1 Lời giải chi tiết :
\(q = {Q_0}\cos (\omega t + \varphi )\) Biểu thức của cường độ dòng điện trong mạch: \(i = q' = \omega {Q_0}\cos (\omega t + \varphi + \frac{\pi }{2})\)
Câu 2 :
Phương trình dao động của điện tích trong mạch dao động LC là \(q = {Q_0}\cos (\omega t + \varphi )\). Biểu thức của hiệu điện thế trong mạch là:
Đáp án : B Phương pháp giải :
Xem lí thuyết mục 1 Lời giải chi tiết :
\(q = {Q_0}\cos (\omega t + \varphi )\) Biểu thức của hiện điện thế trong mạch là: \(u = \frac{{{Q_0}}}{C}\cos (\omega t + \varphi )\)
Câu 3 :
Biểu thức của cường độ dòng điện trong mạch dao động LC là \(i = {I_0}\cos (\omega t + \varphi )\). Biểu thức của điện tích trong mạch là:
Đáp án : B Phương pháp giải :
+ Áp dụng độ lệch pha giữa cường độ dòng điện và điện tích + Áp dụng biểu thức mối liên hệ giữa cường độ dòng điện cực đại và điện tích cực đại : \({I_0} = \omega {q_0}\) Lời giải chi tiết :
Ta có , điện tích q trễ pha hơn cường độ dòng điện 1 góc π/2 và \({I_0} = \omega {q_0}\) \(i = {I_0}\cos (\omega t + \varphi ) \to q = \frac{{{I_0}}}{\omega }\cos (\omega t + \varphi - \frac{\pi }{2})\)
Câu 4 :
Một mạch dao động gồm một tụ điện có điện dung \(C = 10 pF\) và cuộn dây thuần cảm có độ tự cảm \(L = 0,25 mH\), cường độ dòng điện cực đại là \(50 mA\). Tại thời điểm ban đầu cường độ dòng điện qua mạch bằng không. Biểu thức của điện tích trên tụ là:
Đáp án : D Phương pháp giải :
- Cách 1: + Áp dụng công thức tính tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }}\) + Áp dụng công thức tính điện tích cực đại trên bản tụ: \({q_0} = \dfrac{{{I_0}}}{\omega }\) + Xác định \(\varphi \), tại \(t{\rm{ }} = {\rm{ }}0\): \(q = {q_0}cos\varphi \) - Cách 2: + Sử dụng vòng tròn lượng giác + Ta có: \(i = q'\) => điện tích \(q\) trễ pha \(\dfrac{\pi }{2}\) so với cường độ dòng điện hay \({\varphi _q} = {\varphi _i} - \dfrac{\pi }{2}\) + Viết phương trình điện tích \(q = {q_0}cos\left( {\omega t + {\varphi _q}} \right)\) Lời giải chi tiết :
+ Tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {0,{{25.10}^{ - 3}}{{.10.10}^{ - 12}}} }} = {2.10^7}(ra{\rm{d}}/s)\) + Điện tích cực đại trên tụ: \({q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{{{50.10}^{ - 3}}}}{{{{2.10}^7}}} = 2,{5.10^{ - 9}}C\) + Tại t = 0: \(i = 0 \to q = {q_{max}} = {q_0} = {q_0}c{\rm{os}}\varphi \to c{\rm{os}}\varphi {\rm{ = 1}} \to \varphi {\rm{ = 0}}\) => \(q{\text{ }} = {\text{ }}2,{5.10^{ - 9}}cos\left( {{{2.10}^7}t} \right){\text{ }}C\) Cách 2: Ta có: + Tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {0,{{25.10}^{ - 3}}{{.10.10}^{ - 12}}} }} = {2.10^7}(ra{\rm{d}}/s)\) + Cường độ dòng điện cực đại: \({I_0} = \omega {q_0} \to {q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{{{50.10}^{ - 3}}}}{{{{2.10}^7}}} = 2,{5.10^{ - 9}}C\) + Tại thời điểm ban đầu \(t = 0\), \(i = 0\) và đang tăng, vẽ trên vòng tròn lượng giác, ta được: 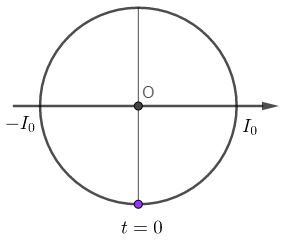 \( \to {\varphi _i} = - \dfrac{\pi }{2}\) \( \to {\varphi _q} = {\varphi _i} - \dfrac{\pi }{2} = \dfrac{\pi }{2} - \dfrac{\pi }{2} = 0\) => Phương trình điện áp: \(q = {q_0}cos\left( {\omega t + {\varphi _q}} \right) = 2,{5.10^{ - 9}}cos\left( {{{2.10}^7}t} \right)C\)
Câu 5 :
Cho mạch dao động điện từ tự do gồm tụ điện có điện dung C = 1μF. Biết biểu thức cường độ dòng điện trong mạch là i = 20cos(1000t + π/2) mA. Biểu thức điện áp giữa hai bản tụ điện có dạng:
Đáp án : C Phương pháp giải :
+ Đọc phương trình cường độ dòng điện + Áp dụng công thức tính tần số góc : \(\omega = \frac{1}{{\sqrt {LC} }}\) + Áp dụng biểu thức mối liên hệ giữa hiệu điện thế cực đại và cường độ dòng điện cực đại: \({U_0} = {I_0}\sqrt {\frac{L}{C}} \) + Áp dụng biểu thức mối liên hệ giữa pha của cường độ dòng điện và điện áp giữa 2 bản tụ : \({\varphi _i} = {\varphi _u} + \frac{\pi }{2}\) Lời giải chi tiết :
Từ phương trình : i = 20cos(1000t + π/2) mA, ta có: + Tần số góc: \(\omega = 1000 = \frac{1}{{\sqrt {LC} }} \to L = \frac{1}{{{\omega ^2}C}} = \frac{1}{{{{1000}^2}{{.10}^{ - 6}}}} = 1H\) + Cường độ dòng điện cực đại: I0 = 20mA - Ta có: \(CU_0^2 = LI_0^2 \to {U_0} = \sqrt {\frac{{LI_0^2}}{C}} = \sqrt {{{\frac{{1.({{20.10}^{ - 3}})}}{{{{10}^{ - 6}}}}}^2}} = 20V\) - Dòng điện trong mạch dao động nhanh pha\(\frac{\pi }{2}\) so với điện áp trong mạch: \({\varphi _i} = {\varphi _u} + \frac{\pi }{2} \to {\varphi _u} = {\varphi _i} - \frac{\pi }{2} = \frac{\pi }{2} - \frac{\pi }{2} = 0\) => u = 20cos(1000t) V
Câu 6 :
Một mạch dao động LC có điện áp 2 bản tụ là u = 5cos(104t) V, điện dung C = 0,4 μF. Biểu thức cường độ dòng điện trong mạch là :
Đáp án : B Phương pháp giải :
+ Đọc phương trình cường độ dòng điện + Áp dụng công thức tính tần số góc : \(\omega = \frac{1}{{\sqrt {LC} }}\) + Áp dụng biểu thức mối liên hệ giữa hiệu điện thế cực đại và cường độ dòng điện cực đại: \({I_0} = {U_0}\sqrt {\frac{C}{L}} \) + Áp dụng biểu thức mối liên hệ giữa pha của cường độ dòng điện và điện áp giữa 2 bản tụ : \({\varphi _i} = {\varphi _u} + \frac{\pi }{2}\) Lời giải chi tiết :
Từ phương trình : u = 5cos(104t) V, ta có: + Tần số góc: \(\omega = {10^4} = \frac{1}{{\sqrt {LC} }} \to L = \frac{1}{{{\omega ^2}C}} = \frac{1}{{{{({{10}^4})}^2}.0,{{4.10}^{ - 6}}}} = 0,025H\) + Hiệu điện thế cực đại: U0 = 5V - Ta có: \(CU_0^2 = LI_0^2 \to {I_0} = \sqrt {\frac{{CU_0^2}}{L}} = \sqrt {{{\frac{{0,{{4.10}^{ - 6}}5}}{{0,025}}}^2}} = 0,02A\) - Dòng điện trong mạch dao động nhanh pha\(\frac{\pi }{2}\) so với điện áp trong mạch: \({\varphi _i} = {\varphi _u} + \frac{\pi }{2} = 0 + \frac{\pi }{2} = \frac{\pi }{2}\) => i = 2.10-2cos(104t + π/2) A
Câu 7 :
Mạch dao động gồm tụ điện có điện dung \(C = 10nF\)và cuộn dây thuần cảm có hệ số tử cảm \(L = {10_{}}mH\). Tụ điện được tích điện đến hiệu điện thế 12V. Sau đó cho tụ phóng điện trong mạch. Lấy \({\pi ^2} = 10\) và gốc thời gian là lúc tụ bắt đầu phóng điện. Biểu thức của dòng điện trong cuộn cảm là :
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính tần số góc: \(\omega = \frac{1}{{\sqrt {LC} }}\) + Áp dụng biểu thức mối liên hệ giữa cường độ dòng điện cực đại và hiệu điện thế cực đại: \({I_0} = {U_0}\sqrt {\frac{C}{L}} \) + Xác định pha ban đầu của dao động Lời giải chi tiết :
Ta có: + Tần số góc của dao động: \(\omega = \frac{1}{{\sqrt {LC} }} = \frac{1}{{\sqrt {{{10.10}^{ - 3}}{{.10.10}^{ - 9}}} }} = {10^5}(ra{\rm{d}}/s)\) + Cường độ dòng điện cực đại: \({I_0} = {U_0}\sqrt {\frac{C}{L}} = 12\sqrt {\frac{{{{10.10}^{ - 9}}}}{{{{10.10}^{ - 3}}}}} = {12.10^{ - 3}}A\) + Tại t = 0: \(q = {q_0} \to {\varphi _q} = 0\) Ta có: Dòng điện trong mạch dao động nhanh pha\(\frac{\pi }{2}\) so với điện tích trong mạch: \({\varphi _i} = {\varphi _q} + \frac{\pi }{2} = 0 + \frac{\pi }{2} = \frac{\pi }{2}\) => Biểu thức cường độ dòng điện trong mạch: \(i = 12c{\rm{os}}\left( {{{10}^5}t + \frac{\pi }{2}} \right)mA\)
Câu 8 :
Mạch dao động LC gồm cuộn dây thuần cảm có độ tự cảm \(L = 2mH\) và tụ điện có điện dung \(C = 5pF\) Tụ được tích điện đến hiệu điện thế 10V, sau đó người ta để cho tụ phóng điện trong mạch. Nếu chọn gốc thời gian là lúc tụ bắt đầu phóng điện thì biểu thức của điện tích trên bản tụ điện là:
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính tần số góc: \(\omega = \frac{1}{{\sqrt {LC} }}\) + Áp dụng biểu thức: \({U_0} = \frac{{{q_0}}}{C}\) + Xác định pha ban đầu của dao động Lời giải chi tiết :
Ta có: + Tần số góc của dao động: \(\omega = \frac{1}{{\sqrt {LC} }} = \frac{1}{{\sqrt {{{2.10}^{ - 3}}{{.5.10}^{ - 12}}} }} = {10^7}(ra{\rm{d}}/s)\) + Điện tích cực đại: \({U_0} = \frac{{{q_0}}}{C} \to {q_0} = {U_0}C = {10.5.10^{ - 12}} = {5.10^{ - 11}}C\) + Tại t = 0: \(q = {q_0} \to {\varphi _q} = 0\) => Biểu thức điện tích trên bản tụ là: \(q = {5.10^{ - 11}}c{\rm{os}}\left( {{{10}^7}t} \right)C\)
Câu 9 :
Cho mạch điện như hình vẽ. Biết $C = 500 pF$, $L = 0,2mH$, $E = 1,5 V$. Lấy $π^2= 10$. Tại thời điểm $t = 0$, khóa K chuyển từ 1 sang 2. Thiết lập phương trình biểu diễn sự phụ thuộc của điện tích trên tụ điện C theo thời gian? 
Đáp án : B Phương pháp giải :
+ Áp dụng công thức tính tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }}\) + Áp dụng biểu thức: \({U_0} = \dfrac{{{q_0}}}{C}\) + Xác định pha ban đầu của dao động + Viết phương trình điện tích Lời giải chi tiết :
Ta có: + Tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {0,{{2.10}^{ - 3}}{{.500.10}^{ - 12}}} }} = {10^6}\pi (ra{\text{d}}/s)\) + Điện tích cực đại: ${U_0} = \dfrac{{{q_0}}}{C} \to {q_0} = {U_0}C = E.C = 1,{5.500.10^{ - 12}} = 0,{75.10^{ - 9}}C$ Khi K ở vị trí 1 => Tụ được tích điện + Tại t = 0: Khóa K chuyển từ 1 sang 2 => Tụ bắt đầu phóng điện \( \to t = 0:q = {q_0} \to {\varphi _q} = 0\) => Biểu thức điện tích q-t: \(q{\rm{ }} = {\rm{ }}0,75cos({10^6}\pi t){\rm{ }}nC\)
Câu 10 :
Một mạch dao động lí tưởng đang có dao động điện từ tự do với chu kì dao động T. Tại thời điểm t = 0, điện tích trên một bản tụ điện đạt giá trị cực đại. Điện tích trên bản tụ này bằng 0 ở thời điểm đầu tiên (kể từ t = 0) là:
Đáp án : D Phương pháp giải :
Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Khoảng thời gian để điện tích trên bản tụ có giá trị từ q0 đến 0 là: \(\frac{T}{4}\) 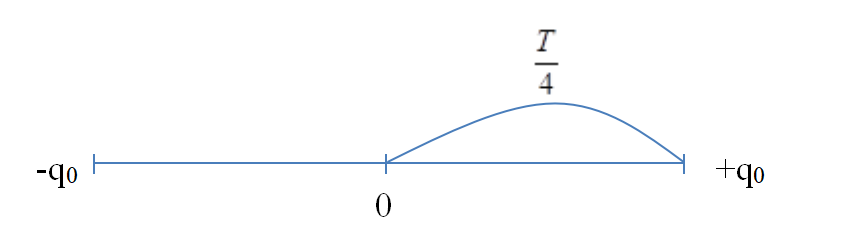
Câu 11 :
Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm 1 H và tụ điện có điện dung 10 μF. Lấy π2 = 10. Lúc đầu, điện tích trên một bản tụ điện đạt giá trị cực đại. Điện tích trên tụ điện có giá trị bằng một nửa giá trị ban đầu sau khoảng thời gian ngắn nhất là:
Đáp án : C Phương pháp giải :
+ Áp dụng công thức tính chu kì dao động của mạch LC: \(T = 2\pi \sqrt {LC} \) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Ta có + Chu kì dao động của mạch: \(T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{1.10.10}^{ - 6}}} = 0,02{\rm{s}}\) + Khoảng thời gian ngắn nhất đi từ q0 đến q0/2 là : \(\frac{T}{6} = \frac{{0,02}}{6} = \frac{1}{{300}}s\) 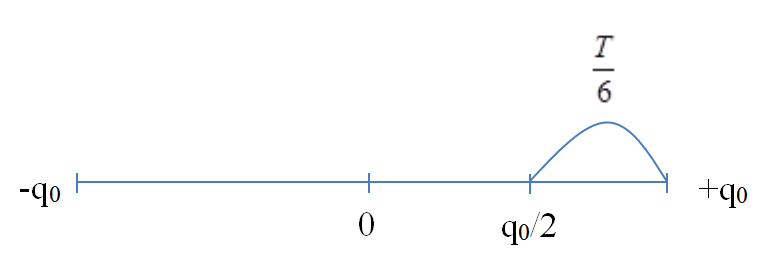
Câu 12 :
Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm 5μH và tụ điện có điện dung 5 μF. Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính chu kì dao động của mạch LC: \(T = 2\pi \sqrt {LC} \) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Ta có + Chu kì dao động của mạch: \(T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{5.10}^{ - 6}}{{.5.10}^{ - 6}}} = 10\pi {.10^{ - 6}}{\rm{s}}\) + Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên bản tụ có độ lớn cực đại là : \(\frac{T}{2} = \frac{{10\pi {{.10}^{ - 6}}}}{2} = 5\pi {.10^{ - 6}}s\) 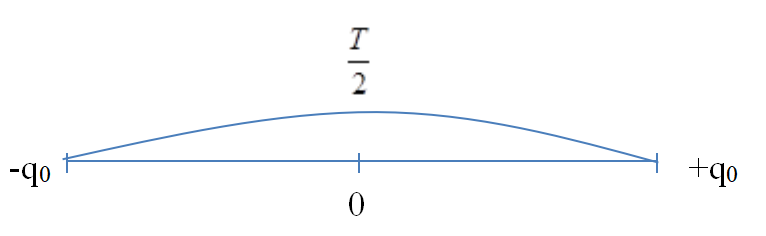
Câu 13 :
Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Tại thời điểm t = 0, điện tích trên một bản tụ điện cực đại. Sau khoảng thời gian ngắn nhất Δt thì điện tích trên bản tụ này bằng một nửa giá trị cực đại. Chu kì dao động riêng của mạch dao động này là:
Đáp án : B Phương pháp giải :
Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Khoảng thời gian ngắn nhất điện tích từ q0 về q0/2: \(\Delta t = \frac{T}{6} \to T = 6\Delta t\) 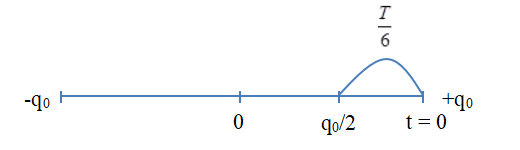
Câu 14 :
Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại trên một bản tụ điện là \(4\sqrt 2 \mu C\) và cường độ dòng điện cực đại trong mạch là \(0,5\sqrt 2 \pi A\) Thời gian ngắn nhất để điện tích trên một bản tụ giảm từ q0 đến \(\frac{{{q_0}}}{{\sqrt 2 }}\) là:
Đáp án : D Phương pháp giải :
+ Áp dụng biểu thức mối liên hệ giữa cường độ dòng điện cực đại và điện tích cực đại: \({I_0} = \omega {q_0}\) + Áp dụng công thức tính chu kì dao động trong mạch LC: \(T = \frac{{2\pi }}{\omega }\) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Ta có: + \({I_0} = \omega {q_0} \to \omega = \frac{{{I_0}}}{{{q_0}}} = \frac{{0,5\sqrt 2 \pi }}{{4\sqrt 2 {{.10}^{ - 6}}}} = 125000\pi \) + Chu kì dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{125000\pi }} = 1,{6.10^{ - 5}}s\) + Thời gian ngắn nhất để điện tích trên một bản tụ giảm từ q0 đến \(\frac{{{q_0}}}{{\sqrt 2 }}\) là: \(\frac{T}{8} = \frac{{1,{{6.10}^{ - 5}}}}{8} = {2.10^{ - 6}}s\) 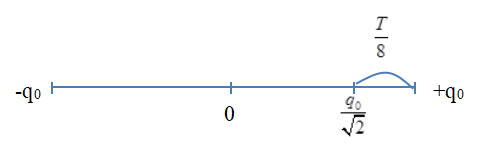
Câu 15 :
Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do, thời điểm ban đầu điện tích trên tụ điện đạt giá trị cực đại q0 = 10-8 C. Thời gian ngắn nhất để tụ phóng hết điện tích là 2 μs. Cường độ hiệu dụng của dòng điện trong mạch là:
Đáp án : A Phương pháp giải :
+ Sử dụng trục thời gian suy ra từ vòng tròn + Áp dụng công thức tính tần số góc: \(\omega = \frac{{2\pi }}{T}\) + Áp dụng biểu thức mối liên hệ giữa cường độ dòng điện cực đại và điện tích cực đại: \({I_0} = \omega {q_0}\) Lời giải chi tiết :
Ta có, thời gian ngắn nhất để tụ phóng hết điện tích từ q = q0 (thời gian đi từ q0 đến 0) là: \(t = \frac{T}{4} = 2\mu s \to T = 8\mu s\) Tần số góc: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{{{8.10}^{ - 6}}}} = 25\pi {.10^4}(ra{\rm{d}}/s)\) Cường độ dòng điện cực đại: \({I_0} = \omega {q_0} = 25\pi {.10^4}{.10^{ - 8}} \approx 7,{85.10^{ - 3}}mA\) => Cường độ dòng điện hiệu dụng:$I = \frac{{{I_0}}}{{\sqrt 2 }} = \frac{{{{7,85.10}^{ - 3}}}}{{\sqrt 2 }} = {5,55.10^{ - 3}}A = 5,55mA$
Câu 16 :
Một mạch dao động điện từ LC lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại trên một bản tụ điện là q0 = 1μC và cường độ dòng điện cực đại trong mạch là I0 = 3π mA. Tính từ thời điểm điện tích trên tụ là q0 , khoảng thời gian ngắn nhất để dòng điện trong mạch có độ lớn bằng I0 là:
Đáp án : D Phương pháp giải :
+ Áp dụng biểu thức mối liên hệ giữa cường độ dòng điện cực đại và điện tích cực đại: \({I_0} = \omega {q_0}\) + Áp dụng biểu thức: \(T = \frac{{2\pi }}{\omega }\) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Ta có: \({I_0} = \omega {q_0} \to \omega = \frac{{{I_0}}}{{{q_0}}} = \frac{{3\pi {{.10}^{ - 3}}}}{{{{10}^{ - 6}}}} = 3\pi {.10^3}(ra{\rm{d}}/s)\) Chu kì dao động của mạch: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{3\pi {{.10}^3}}} = \frac{2}{3}{10^{ - 3}}s\) Tại thời điểm q = q0 thì cường độ dòng điện i = 0 (do cường độ dòng điện và điện tích lệch pha nhau 900) => Khoảng thời gian ngắn nhất để i = 0 đến i = I0 là \(\frac{T}{4} = \frac{{\frac{2}{3}{{.10}^{ - 3}}}}{4} = \frac{1}{6}{.10^{ - 3}}s\)
Câu 17 :
Khi điện tích trên tụ tăng từ $0$ lên $0,5{\rm{ }}\left( {\mu C} \right)$ thì đồng thời cường độ dòng điện trong mạch dao động LC lí tưởng giảm từ $3\pi \left( {mA} \right)$ xuống \(\dfrac{{3\sqrt 3 \pi }}{2}mA\) . Khoảng thời gian xảy ra sự biến thiên này là:
Đáp án : D Phương pháp giải :
+ Sử dụng vòng tròn lượng giác + Áp dụng công thức mối liên hệ giữa q0 và I0: \(\omega = \dfrac{{{I_0}}}{{{q_0}}}\) + Áp dụng công thức: \(\Delta \varphi = \omega \Delta t\) Lời giải chi tiết :
Ta có: - Khi $q = 0,i = 3\pi (mA) = {I_0}$ => khi \(i = \dfrac{{3\sqrt 3 \pi }}{2}mA = \dfrac{{{I_0}\sqrt 3 }}{2}\) Vẽ vòng tròn lượng giác, ta được: 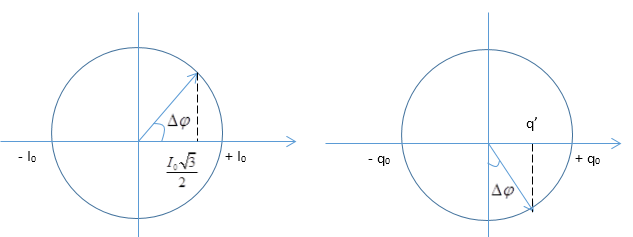 Từ vòng tròn lượng giác, ta có: ${\rm{cos}}\Delta \varphi {\rm{ = }}\dfrac{{\dfrac{{{I_0}\sqrt 3 }}{2}}}{{{I_0}}} = \dfrac{{\sqrt 3 }}{2} \to \Delta \varphi = \dfrac{\pi }{6}$ \(\begin{array}{l} \to q' = {q_0}\sin \Delta \varphi = {q_0}\sin \dfrac{\pi }{6} = \dfrac{{{q_0}}}{2} = 0,5\mu C \to {q_0} = 1\mu C\\ \to \omega = \dfrac{{{I_0}}}{{{q_0}}} = \dfrac{{3\pi {{.10}^{ - 3}}}}{{{{10}^{ - 6}}}} = 3\pi {.10^3}({\rm{r}}a{\rm{d}}/s)\end{array}\) Ta có: \(\Delta \varphi = \omega \Delta t \to \Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{\pi }{6}}}{{3\pi {{.10}^3}}} = \dfrac{1}{{18}}{.10^{ - 3}} = \dfrac{1}{{18}}ms\)
Câu 18 :
Trong mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Biết thời gian để cường độ dòng điện trong mạch giảm từ giá trị cực đại I0 = 2,22 A xuống còn một nửa là τ = 8/3 (μs). Ở những thời điểm cường độ dòng điện trong mạch bằng không thì điện tích trên tụ bằng:
Đáp án : B Phương pháp giải :
+ Sử dụng trục thời gian suy ra từ vòng tròn + Áp dụng công thức tính tần số góc: \(\omega = \frac{{2\pi }}{T}\) + Áp dụng công thức tính điện tích cực đại trên bản tụ: \({q_0} = \frac{{{I_0}}}{\omega }\) Lời giải chi tiết :
Ta có khoảng thời gian để cường độ dòng điện trong mạch giảm từ I0 đến I0/2 là: \(\tau = \frac{T}{6} = \frac{8}{3}\mu s \to T = 16\mu s\) Tần số góc: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{{{16.10}^{ - 6}}}} = 12,5\pi {.10^4}(ra{\rm{d}}/s)\) - Khi i = 0 thì q = q0 : do cường độ dòng điện và điện tích lệch pha nhau một góc π/2 Ta có, \({q_0} = \frac{{{I_0}}}{\omega } = \frac{{2,22}}{{12,5\pi {{.10}^4}}} = 5,{65.10^{ - 6}}C\)
Câu 19 :
Trong mạch dao động lí tưởng đang có dao động điện từ tự do với chu kỳ T. Biết tụ điện có điện dung \(2nF\) và cuộn cảm có độ tự cảm \(8mH\). Tại thời điểm t1, cường độ dòng điện trong mạch có độ lớn \(5 mA\). Tại thời điểm t2 = t1 + 2π.10-6(s) điện áp giữa hai bản tụ có độ lớn
Đáp án : A Phương pháp giải :
Chu kỳ mạch dao động LC là: \(T = 2\pi \sqrt {LC} \) Liên hệ giữa điện áp cực đại và dòng điện cực đại: \(CU_0^2 = LI_0^2\) Điện tích cực đại q0 = CU0 Mạch LC có u và i vuông pha nhau Lời giải chi tiết :
Chu kỳ mạch dao động LC là: \(T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{8.10}^{ - 3}}{{.2.10}^{ - 9}}} = 8\pi {.10^{ - 6}}(s) \Rightarrow \omega = 2,{5.10^5}rad/s\) Ta có: \(CU_0^2 = LI_0^2 \Rightarrow {U_0} = \sqrt {\dfrac{{LI_0^2}}{C}} = 2000{I_0}\) ZL = 2000Ω; ZC = 2000Ω nên u và i cùng pha nhau Ở thời điểm t1 có i1 = ωq0cos(ωt1) = ωCU0cos(ωt1) = 5mA Ở thời điểm t2 có u2 = \({U_0}{\rm{cos}}\left[ {\omega ({t_1} + \dfrac{T}{4}) - \dfrac{\pi }{2}} \right] = {U_0}{\rm{cos}}\omega {{\rm{t}}_1} = \dfrac{{{i_1}}}{{\omega C}} = \dfrac{{{{5.10}^{ - 3}}}}{{2,{{5.10}^5}{{.2.10}^{ - 9}}}} = 10V\)
Câu 20 :
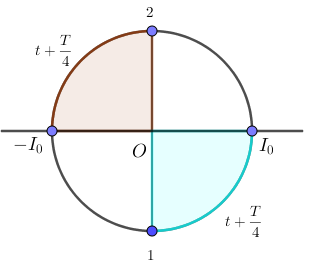
Một mạch dao động lí tưởng gồm cuộn cảm thuần có độ tư cảm \(L\) và tụ điện có điện dung \(C\) đang có dao động điện từ tự do. Ở thời điểm \(t\), dòng điện qua cuộn dây có cường độ bằng \(0\) thì ở thời điểm \(t + \dfrac{{\pi \sqrt {LC} }}{2}\)
Đáp án : C Phương pháp giải :
Xác định giá trị i, u, q tại thời điểm \(t + \dfrac{{\pi \sqrt {LC} }}{2}\) Lời giải chi tiết :
Ta có, tại thời điểm t cường độ dòng điện \(i = 0A\) (có thể ở vị trí 1 hoặc 2 như hình vẽ) Ở thời điểm \(t + \dfrac{{\pi \sqrt {LC} }}{2} = t + \dfrac{T}{4}\) + Ứng với vị trí 1 => tại thời điểm \(t + \dfrac{T}{4}\) cường độ dòng điện \(i = {I_0}\) + Ứng với vị trí 2 => tại thời điểm \(t + \dfrac{T}{4}\) cường độ dòng điện \(i = - {I_0}\)
\(\Rightarrow \left| i \right| = {I_0}\) và \(u = 0,q = 0\) \( \Rightarrow \) Năng lượng điện trường: \({{\rm{W}}_d} = \dfrac{{{q^2}}}{{2C}} = 0\)
Câu 21 :
Một mạch dao động LC lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C đang có dao động điện từ tự do. Điện tích trên một bản tụ ở thời điểm t có dạng biểu thức \(q = {q_0}cos\left( {\omega t + \frac{\pi }{2}} \right)\left( C \right)\) (t tính bằng giây). Kể từ thời điểm ban đầu \(t = 0\), sau khoảng thời gian ngắn nhất \({10^{ - 6}}s\) thì điện tích trên bản tụ bằng 0. Tần số dao động của mạch này là
Đáp án : C Phương pháp giải :
+ Đọc phương trình điện tích + Sử dụng trục thời gian suy ra từ vòng tròn lượng giác Lời giải chi tiết :
Biểu thức điện tích: \(q = {q_0}co{\rm{s}}\left( {\omega t + \frac{\pi }{2}} \right)\left( C \right)\) Tại \(t = 0\) có \(q = 0\)
Thời gian ngắn nhất kể từ \(t = 0\) đến khi điện tích trên tụ bằng 0 là: \(\Delta t = \frac{T}{2} = {10^{ - 6}}s \Rightarrow T = {2.10^{ - 6}}s\) Tần số: \(f = \frac{1}{T} = 500000H{\rm{z}} = 500kH{\rm{z}}\)
Câu 22 :
Cường độ dòng điện tức thời trong một mạch dao động là \(i = 0,05\cos 100\pi t\) (A). Hệ số tự cảm của cuộn dây là 2mH. Lấy \({\pi ^2} = 10\). Điện dung và biểu thức điện tích của tụ điện có giá trị nào sau đây?
Đáp án : D Phương pháp giải :
Sử dụng các công thức: \(\left\{ \begin{array}{l}\omega = \frac{1}{{\sqrt {LC} }}\\{\rm{W}} = \frac{{LI_0^2}}{2} = \frac{{CU_0^2}}{2} = \frac{{Q_0^2}}{{2C}}\end{array} \right.\) Lời giải chi tiết :
Ta có: \(\omega = \frac{1}{{\sqrt {LC} }} \Leftrightarrow 100\pi = \frac{1}{{\sqrt {{{2.10}^{ - 3}}.C} }}\) \( \Rightarrow C = {5.10^{ - 3}}F\) Lại có: \(\frac{{LI_0^2}}{2} = \frac{{Q_0^2}}{{2C}} \Leftrightarrow Q_0^2 = LI_0^2C\) \({Q_0} = {I_0}\sqrt {LC} = 0,05.\frac{1}{{100\pi }} = \frac{{{{5.10}^{ - 4}}}}{\pi }\left( C \right)\) Mặt khác, q trễ pha hơn i góc \(\frac{\pi }{2}\) suy ra \({\varphi _q} = 0 - \frac{\pi }{2} = - \frac{\pi }{2}\) Vậy \(q = \frac{{{{5.10}^{ - 4}}}}{\pi }\cos \left( {100\pi t - \frac{\pi }{2}} \right)\left( C \right)\)
Câu 23 :
Trong mạch dao động LC lý tưởng, đại lượng nào không thỏa mãn phương trình vi phân dạng \(x'' - {\omega ^2}x = 0\), với \(\omega = \dfrac{1}{{\sqrt {LC} }}\).
Đáp án : B Phương pháp giải :
Điện tích, cường độ dòng điện, hiệu điện thế của mạch dao động có tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }}\) Năng lượng trên tụ điện và cuộn cảm dao đông với tần số góc: \(\omega ' = 2\omega = \dfrac{2}{{\sqrt {LC} }}\) Lời giải chi tiết :
Năng lượng trên tụ điện dao động với tần số góc \(\omega = \dfrac{2}{{\sqrt {LC} }}\) \( \Rightarrow \) Tần số góc \(\omega = \dfrac{1}{{\sqrt {LC} }}\) không phải là tần số của năng lượng tụ điện.
Câu 24 :
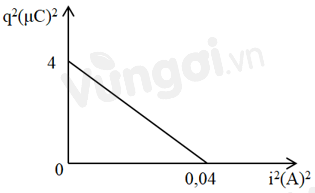
Một mạch dao động LC lí tưởng với \(q\) là điện tích trên tụ, \(i\) là dòng điện tức thời trong mạch. Đồ thị thể hiện sự phụ thuộc của \({q^2}\) vào \({i^2}\) như hình vẽ. Bước sóng mà mạch thu được trong không khí là
Đáp án : D Phương pháp giải :
+ Biểu điện điện tích và cường độ dòng điện: \(\left\{ \begin{array}{l}q = {Q_0}.cos\left( {\omega t + \varphi } \right)\\i = {I_0}.cos\left( {\omega t + \varphi + \frac{\pi }{2}} \right)\end{array} \right.\) + Biểu thức vuông pha của q và i: \({\left( {\dfrac{q}{{{Q_0}}}} \right)^2} + {\left( {\dfrac{i}{{{I_0}}}} \right)^2} = 1\) + Mối liên hệ giữa điện tích cực đại và cường độ dòng điện cực đại: \({I_0} = \omega {Q_0}\) + Bước sóng: \(\lambda = \dfrac{{2\pi c}}{\omega }\) Lời giải chi tiết :
Từ đồ thị ta thấy: + Tại \(\left\{ \begin{array}{l}{i^2} = 0\\{q^2} = 4{\left( {\mu C} \right)^2}\end{array} \right. \Rightarrow Q_0^2 = 4{\left( {\mu C} \right)^2} \Rightarrow {Q_0} = 2\mu C\) + Tại: \(\left\{ {\begin{array}{*{20}{l}}{{q^2} = 0}\\{{i^2} = 0,04{\mkern 1mu} {\mkern 1mu} {{\left( A \right)}^2}}\end{array}} \right. \Rightarrow I_0^2 = 0,04{\mkern 1mu} {\mkern 1mu} {\left( A \right)^2} \Rightarrow {I_0} = 0,2{\mkern 1mu} {\mkern 1mu} \left( A \right)\) \( \Rightarrow \omega {\rm{}} = \dfrac{{{I_0}}}{{{Q_0}}} = \dfrac{{0,2}}{{{{2.10}^{ - 6}}}} = {1.10^5}{\mkern 1mu} {\mkern 1mu} \left( {rad/s} \right)\) Bước sóng mà mạch thu được trong không khí là: \(\lambda = \dfrac{{2\pi c}}{\omega } = \dfrac{{2\pi {{.3.10}^8}}}{{{{1.10}^5}}} = 6\pi {.10^3}\,\,\left( m \right)\)
|



















Danh sách bình luận