Trắc nghiệm Bài 1. Dao động điều hòa - Các đại lượng đặc trưng - Vật Lí 12Đề bài
Câu 1 :
Một vật dao động điều hòa với phương trình $x=Acos(ωt+φ)$. $A$ được gọi là:
Câu 2 :
Một vật dao động điều hoà theo phương trình \(x = 2cos\left( {5\pi t + \frac{{7\pi }}{3}} \right)cm\). Biên độ dao động của vật là:
Câu 3 :
Phương trình dao động điều hòa của một chất điểm có dạng \(x = {\rm{ }}Acos\left( a \right)t\) .Độ dài quỹ đạo của dao động là:
Câu 4 :
Một chất điểm dao động điều hoà trên quỹ đạo $MN = 30 cm$, biên độ dao động của vật là:
Câu 5 :
Một vật dao động điều hòa với phương trình $x=Acos(ωt+φ)$. Pha dao động tại thời điểm $t$ là:
Câu 6 :
Một vật dao động điều hòa theo phương trình x = 3cos(7πt + π) cm, pha dao động tại thời điểm t = 1 (s) là:
Câu 7 :
Một vật dao động điều hoà theo phương trình \(x = {\rm{ }}-5cos(5\pi t{\rm{ }} - 7\pi /6)cm\). Biên độ dao động và pha ban đầu của vật là:
Câu 8 :
Một vật dao động điều hòa thực hiện được N dao động trong thời gian ∆t giây. Chu kỳ dao động của vật là:
Câu 9 :
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\), chu kỳ dao động của chất điểm được xác định bởi:
Câu 10 :
Một vật dao động điều hòa trong thời gian $20$ giây vật thực hiện được $80$ dao động toàn phần. Chu kỳ dao động của vật là:
Câu 11 :
Một con lắc lò xo dao động với phương trình $x = 6c{\text{os}}\left( {20\pi t } \right)cm$. Xác định chu kỳ, tần số dao động của chất điểm.
Câu 12 :
Chất điểm dao động điều hòa với phương trình \(x = 6cos\left( {10t - \dfrac{{3\pi }}{2}} \right)cm\). Li độ của chất điểm khi pha dao động bằng \(\dfrac{{2\pi }}{3}\) là:
Câu 13 :
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\). Biểu thức vận tốc tức thời của chất điểm là:
Câu 14 :
Một vật dao động điều hòa có phương trình \(x = 2cos\left( {2\pi t - \frac{{7\pi }}{6}} \right){\rm{ }}cm\). Li độ của vật tại thời điểm $t = 0,25 (s)$ là:
Câu 15 :
Một chất điểm dao động điều hòa với phương trình $x = Ac{\text{os}}\left( {\omega t + \varphi } \right)$. Tốc độ cực đại vật đạt được trong quá trình dao động là:
Câu 16 :
Một chất điểm dao động điều hoà với phương trình dạng \(x = 5cos(7\pi t{\rm{ }} + \dfrac{{7\pi }}{6})cm\). Biểu thức vận tốc tức thời của chất điểm là:
Câu 17 :
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\). Biểu thức gia tốc tức thời của chất điểm là:
Câu 18 :
Biểu thức nào sau đây là biểu thức tính gia tốc của một vật dao động điều hòa?
Câu 19 :
Một vật dao động điều hoà chu kỳ T. Gọi \({v_{max}}\) và \({a_{max}}\) tuơng ứng là vận tốc cực đại và gia tốc cực đại của vật. Hệ thức liên hệ sai giữa \({v_{max}}\) và \({a_{max}}\) là:
Câu 20 :
Một chất điểm dao động điều hòa có tần số góc \(\omega \), tại thời điểm t chất điểm có li độ \(x{\rm{ }}\left( {cm} \right)\) và vận tốc \(v{\rm{ }}\left( {cm/s} \right)\). Biên độ dao động điều hòa của chất điểm là:
Câu 21 :
Một vật dao động điều hòa có biên độ là \(2{\rm{ }}\left( {cm} \right)\) và tần số góc \(\omega = 2\pi \left( {rad} \right)\) . Lấy \({\pi ^2} = 10\), gia tốc của vật tại thời điểm vật có vận tốc \(v = 2\sqrt 3 \pi cm/s\) là:
Câu 22 :
Một vật dao động điều hòa có phương trình \(x = 5cos(2\pi t)\). Vận tốc của vật khi có li độ $x=3 cm$ là:
Câu 23 :
Một vật dao động điều hòa có phương trình \(x = 5cos(2\pi t - \frac{\pi }{6})cm\). Lấy \({\pi ^2} = 10\). Gia tốc của vật khi có li độ $x= 3 cm$ là:
Câu 24 :
Một vật dao động điều hoà với phương trình \(x = {\rm{ }}Acos(\omega t{\rm{ }} + \varphi )\), tại thời điểm $t = 0$ thì li độ $x=A$. Pha ban đầu của dao động là:
Câu 25 :
Dao động điều hoà có vận tốc cực đại là \({v_{max}} = 8\pi cm/s\) và gia tốc cực đại \({a_{max}} = 16{\pi ^2}cm/{s^2}\) thì tần số của dao động là:
Câu 26 :
Dao động điều hoà có vận tốc cực đại là \({v_{max}} = 16\pi cm/s\) và gia tốc cực đại \({a_{max}} = 64{\pi ^2}cm/{s^2}\) thì biên độ của dao động là:
Câu 27 :
Một chất điểm dao động điều hoà với phương trình dạng\(x=cos(2\pi t + \dfrac{\pi}{6})(cm,s)\). Lấy \(\pi ^2 =10\), biểu thức gia tốc tức thời của chất điểm là:
Câu 28 :
Một vật thực hiện dao động điều hòa trên đoạn thẳng dài 12cm. Thời gian để vật đi được đoạn đường dài 24cm là 2s. Tốc độ của vật khi đi qua vị trí cân bằng là
Câu 29 :
Một điểm M chuyển động tròn đều trên một đường tròn với tốc độ 15 cm/s. Gọi P là hình chiếu của M lên một đường kính của đường tròn quỹ đạo. Tốc độ trung bình của P trong một dao động toàn phần bằng
Câu 30 :
Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là
Câu 31 :
Đề thi thử THPT chuyên Lam Sơn - 2021 Một chất điểm dao động theo phương trình \(x = 6co{\rm{s}}\omega {\rm{t}}\left( {cm} \right)\). Dao động của chất điểm có biên độ là
Lời giải và đáp án
Câu 1 :
Một vật dao động điều hòa với phương trình $x=Acos(ωt+φ)$. $A$ được gọi là:
Đáp án : C Lời giải chi tiết :
Ta có: x=Acos(ωt+φ) + x: li độ dao động của vật + A: Biên độ dao động của vật + ω: Tần số góc của dao động + φ: Pha ban đầu của dao động + ωt+φ: Pha dao động tại thời điểm t
Câu 2 :
Một vật dao động điều hoà theo phương trình \(x = 2cos\left( {5\pi t + \frac{{7\pi }}{3}} \right)cm\). Biên độ dao động của vật là:
Đáp án : C Phương pháp giải :
Đồng bộ hóa với phương trình dao động điều hòa: \(x = Acos(\omega t + \varphi )\) Lời giải chi tiết :
Ta có: \(x = Acos(\omega t + \varphi )\) PT đầu bài: \(x = 2cos(5\pi t{\rm{ }} + {\rm{ }}\frac{{7\pi }}{3})cm\) => Biên độ dao động của vật: \(A = 2cm\)
Câu 3 :
Phương trình dao động điều hòa của một chất điểm có dạng \(x = {\rm{ }}Acos\left( a \right)t\) .Độ dài quỹ đạo của dao động là:
Đáp án : B Phương pháp giải :
Đồng bộ hóa với phương trình dao động điều hòa và sử dụng công thức xác định quỹ đạo của vật trong dao động điều hòa. $x = A\cos \left( {\omega t + \varphi } \right)$ Lời giải chi tiết :
Ta có: + \(x = Acos\left( a \right)t\) + Độ dài quỹ đạo của dao động là: \(L = 2A\)
Câu 4 :
Một chất điểm dao động điều hoà trên quỹ đạo $MN = 30 cm$, biên độ dao động của vật là:
Đáp án : C Phương pháp giải :
Sử dụng công thức tính quỹ đạo của vật trong dao động điều hòa: $L=2A$ Lời giải chi tiết :
Ta có: Độ dài quỹ đạo của vật trong dao động điều hòa: $L=2A$ <=> $MN=2A=30cm$ $=> A=15cm$
Câu 5 :
Một vật dao động điều hòa với phương trình $x=Acos(ωt+φ)$. Pha dao động tại thời điểm $t$ là:
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết đại cương về phương trình dao động điều hòa: $x=Acos(ωt+φ)$ Lời giải chi tiết :
Ta có: x=Acos(ωt+φ) + x: li độ dao động của vật + A: Biên độ dao động của vật + ω: Tần số góc của dao động + φ: Pha ban đầu của dao động + ωt+φ: Pha dao động tại thời điểm t
Câu 6 :
Một vật dao động điều hòa theo phương trình x = 3cos(7πt + π) cm, pha dao động tại thời điểm t = 1 (s) là:
Đáp án : D Phương pháp giải :
Thay t vào công thức xác định pha dao động tại thời điểm t: ωt+φ Lời giải chi tiết :
Ta có: Pha dao động của vật tại thời điểm t: ωt+φ = 7πt+π => Pha dao động tại thời điểm t=1s là: 7π.1+π=8π
Câu 7 :
Một vật dao động điều hoà theo phương trình \(x = {\rm{ }}-5cos(5\pi t{\rm{ }} - 7\pi /6)cm\). Biên độ dao động và pha ban đầu của vật là:
Đáp án : B Phương pháp giải :
+ Đồng nhất với phương trình dao động điều hòa: $x=Acos(ωt+φ)$ + Sử dụng công thức lượng giác: $-cosα=cos(α+π)$ + Vận dụng lí thuyết đại cương về các đại lượng trong phương trình dao động điều hòa. Lời giải chi tiết :
Ta có: $x = {\text{ }} - 5cos(5\pi t{\text{ }} - \frac{{7\pi }}{6}) = 5cos(5\pi t{\text{ }} - \frac{{7\pi }}{6} + \pi ) = 5cos(5\pi t{\text{ }} - \frac{\pi }{6})cm$ => Biên độ: $A=5 cm$, pha ban đầu: $\varphi = - \frac{\pi }{6}$
Câu 8 :
Một vật dao động điều hòa thực hiện được N dao động trong thời gian ∆t giây. Chu kỳ dao động của vật là:
Đáp án : A Lời giải chi tiết :
Chu kỳ dao động của vật : $T = \frac{{\Delta t}}{N}$ N số dao động vật thực hiện được trong thời gian ∆t giây.
Câu 9 :
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\), chu kỳ dao động của chất điểm được xác định bởi:
Đáp án : B Lời giải chi tiết :
Chu kỳ dao động điều hòa: $T = \dfrac{{2\pi }}{\omega }$
Câu 10 :
Một vật dao động điều hòa trong thời gian $20$ giây vật thực hiện được $80$ dao động toàn phần. Chu kỳ dao động của vật là:
Đáp án : A Phương pháp giải :
Vận dụng công thức xác định chu kỳ dao động của vật theo số dao động vật thực hiện: $T = \dfrac{{\Delta t}}{N}$ Lời giải chi tiết :
Ta có: $T = \dfrac{{\Delta t}}{N}$thay số vào ta được: $T = \dfrac{{\Delta t}}{N} = \dfrac{{20}}{{80}} = 0,25{\text{s}}$
Câu 11 :
Một con lắc lò xo dao động với phương trình $x = 6c{\text{os}}\left( {20\pi t } \right)cm$. Xác định chu kỳ, tần số dao động của chất điểm.
Đáp án : A Phương pháp giải :
Sử dụng công thức xác đinh chu kỳ, tần số dao động điều hòa: $\omega = \dfrac{{2\pi }}{T} = 2\pi f$ Lời giải chi tiết :
Ta có: $\omega = \frac{{2\pi }}{T} = 2\pi f \to \left\{ \begin{gathered}T = \frac{{2\pi }}{\omega } \hfill \\f = \frac{\omega }{{2\pi }} \hfill \\\end{gathered} \right.$ Từ phương trình, ta có: $ω=20π$, thay vào công thức trên => $\left\{ \begin{gathered}T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{20\pi }} = 0,1{\text{s}} \hfill \\f = \frac{\omega }{{2\pi }} = \frac{1}{T} = 10H{\text{z}} \hfill \\\end{gathered} \right.$
Câu 12 :
Chất điểm dao động điều hòa với phương trình \(x = 6cos\left( {10t - \dfrac{{3\pi }}{2}} \right)cm\). Li độ của chất điểm khi pha dao động bằng \(\dfrac{{2\pi }}{3}\) là:
Đáp án : C Phương pháp giải :
Thay pha dao động vào phương trình li độ x của vật Lời giải chi tiết :
Li độ của chất điểm khi pha dao động bằng \(\dfrac{{2\pi }}{3}\) là: \(x = 6cos(\dfrac{{2\pi }}{3}) = - 3{\rm{ }}cm\)
Câu 13 :
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\). Biểu thức vận tốc tức thời của chất điểm là:
Đáp án : B Lời giải chi tiết :
$v = x' = - \omega Asin(\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2})$
Câu 14 :
Một vật dao động điều hòa có phương trình \(x = 2cos\left( {2\pi t - \frac{{7\pi }}{6}} \right){\rm{ }}cm\). Li độ của vật tại thời điểm $t = 0,25 (s)$ là:
Đáp án : D Phương pháp giải :
Thay t vào phương trình li độ của vật \(x = Acos(\omega t + \varphi )\) Lời giải chi tiết :
Li độ của vật tại thời điểm $t =0,25s$ là: \(x = {\text{ }}2cos(2\pi .0,25{\text{ }} - 7\pi /6) = 2c{\text{os(}}\dfrac{{ - 2\pi }}{3}) = - 1cm\)
Câu 15 :
Một chất điểm dao động điều hòa với phương trình $x = Ac{\text{os}}\left( {\omega t + \varphi } \right)$. Tốc độ cực đại vật đạt được trong quá trình dao động là:
Đáp án : A Lời giải chi tiết :
Tốc độ cực đại của vật: ${v_{{\text{max}}}} = A\omega $
Câu 16 :
Một chất điểm dao động điều hoà với phương trình dạng \(x = 5cos(7\pi t{\rm{ }} + \dfrac{{7\pi }}{6})cm\). Biểu thức vận tốc tức thời của chất điểm là:
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết về phương trình vận tốc trong dao động điều hòa: $v = x' = - \omega A\sin (\omega t + \varphi ) = \omega A\cos (\omega t + \varphi + \dfrac{\pi }{2})$ Lời giải chi tiết :
Ta có: $v = x' = - \omega Asin(\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2})$ $\begin{array}{l}x = 5cos(7\pi t + \dfrac{{7\pi }}{6})cm\\\to v = x' = - 7\pi .5sin(7\pi t + \dfrac{{7\pi }}{6})\\ = 35\pi cos(7\pi t + \dfrac{{7\pi }}{6} + \frac{\pi }{2})\\ = 35\pi cos(7\pi t + \dfrac{{5\pi }}{3})cm/s\end{array}$
Câu 17 :
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\). Biểu thức gia tốc tức thời của chất điểm là:
Đáp án : B Lời giải chi tiết :
$a = v' = x'' = - {\omega ^2}Acos(\omega t + \varphi ) = - {\omega ^2}x$
Câu 18 :
Biểu thức nào sau đây là biểu thức tính gia tốc của một vật dao động điều hòa?
Đáp án : D Phương pháp giải :
Đồng nhất với phương trình gia tốc trong dao động điều hòa: $a = v' = x'' = - {\omega ^2}Acos(\omega t + \varphi ) = - {\omega ^2}x$
Lời giải chi tiết :
Ta có: $a = - {\omega ^2}x$
Câu 19 :
Một vật dao động điều hoà chu kỳ T. Gọi \({v_{max}}\) và \({a_{max}}\) tuơng ứng là vận tốc cực đại và gia tốc cực đại của vật. Hệ thức liên hệ sai giữa \({v_{max}}\) và \({a_{max}}\) là:
Đáp án : C Phương pháp giải :
Sử dụng công thức xác định vận tốc cực đại và gia tốc cực đại của vật trong dao động điều hòa. + Vận tốc cực đại: \({v_{{\rm{max}}}} = \omega A\) + Gia tốc cực đại: \({a_{{\rm{max}}}} = {\omega ^2}A\) Lời giải chi tiết :
Ta có: $\left\{ \begin{gathered}{v_{{\text{max}}}} = \omega A \hfill \\{a_{{\text{max}}}} = {\omega ^2}A \hfill \\\end{gathered} \right. \to \left[ \begin{gathered}\frac{{{a_{{\text{max}}}}}}{{{v_{{\text{max}}}}}} = \frac{{{\omega ^2}A}}{{\omega A}} = \omega = \frac{{2\pi }}{T} \hfill \\\frac{{{a_{{\text{max}}}}}}{{{v^2}_{{\text{max}}}}} = \frac{{{\omega ^2}A}}{{{{(\omega A)}^2}}} = \frac{1}{A} \hfill \\\frac{{{a^2}_{{\text{max}}}}}{{{v_{{\text{max}}}}}} = \frac{{{{({\omega ^2}A)}^2}}}{{\omega A}} = {\omega ^3}A \hfill \\\end{gathered} \right.$
Chú ý
Đề bài đang yêu cầu tìm hệ thức sai
Câu 20 :
Một chất điểm dao động điều hòa có tần số góc \(\omega \), tại thời điểm t chất điểm có li độ \(x{\rm{ }}\left( {cm} \right)\) và vận tốc \(v{\rm{ }}\left( {cm/s} \right)\). Biên độ dao động điều hòa của chất điểm là:
Đáp án : A Lời giải chi tiết :
Ta có: Hệ thức độc lập theo thời gian: ${A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}{\text{ }}$
Câu 21 :
Một vật dao động điều hòa có biên độ là \(2{\rm{ }}\left( {cm} \right)\) và tần số góc \(\omega = 2\pi \left( {rad} \right)\) . Lấy \({\pi ^2} = 10\), gia tốc của vật tại thời điểm vật có vận tốc \(v = 2\sqrt 3 \pi cm/s\) là:
Đáp án : C Lời giải chi tiết :
Ta có: ${A^2} = {\frac{a}{{{\omega ^4}}}^2} + \frac{{{v^2}}}{{{\omega ^2}}}$ Thay \(A = 2cm,\omega = 2\pi \left( {rad} \right)\) , \(v = 2\sqrt 3 \pi cm/s\) vào hệ thức trên ta được: \(a = \pm {\omega ^2}\sqrt {{A^2} - \frac{{{v^2}}}{{{\omega ^2}}}} = \pm {\left( {2\pi } \right)^2}\sqrt {{2^2} - \frac{{{{\left( {2\sqrt 3 \pi } \right)}^2}}}{{{{\left( {2\pi } \right)}^2}}}} = \pm 4{\pi ^2}cm/{s^2} = \pm 40cm/{s^2}\)
Câu 22 :
Một vật dao động điều hòa có phương trình \(x = 5cos(2\pi t)\). Vận tốc của vật khi có li độ $x=3 cm$ là:
Đáp án : B Phương pháp giải :
Sử dụng hệ thức độc lập theo thời gian A-x-v: ${A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}{\text{ }}$ Lời giải chi tiết :
Ta có: ${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}{\text{ }} \to {\text{v = }} \pm \omega \sqrt {{A^2} - {x^2}} $ Thay \(A = 5cm,{\rm{ }}x = 3cm\), tần số góc: \(\omega = 2\pi \left( {rad/s} \right)\) $ \to {\text{v}} = \pm 2\pi \sqrt {{5^2} - {3^2}} = \pm 8\pi cm/s \approx \pm 25,12cm/s$
Câu 23 :
Một vật dao động điều hòa có phương trình \(x = 5cos(2\pi t - \frac{\pi }{6})cm\). Lấy \({\pi ^2} = 10\). Gia tốc của vật khi có li độ $x= 3 cm$ là:
Đáp án : B Phương pháp giải :
Sử dụng công thức xác định gia tốc trong dao động điều hòa: a=-ω2x Lời giải chi tiết :
Ta có: \(a = - {\omega ^2}x\) => Tại \(x = 3cm{\rm{ }} = > a = - {(2\pi )^2}.3 = - 12{\pi ^2} = - 120cm/{s^2}\)
Câu 24 :
Một vật dao động điều hoà với phương trình \(x = {\rm{ }}Acos(\omega t{\rm{ }} + \varphi )\), tại thời điểm $t = 0$ thì li độ $x=A$. Pha ban đầu của dao động là:
Đáp án : A Lời giải chi tiết :
Ta có: tại \(t = 0,{\rm{ }}x = Acos\varphi = A \to cos\varphi = 1 \to \varphi = 0\)
Câu 25 :
Dao động điều hoà có vận tốc cực đại là \({v_{max}} = 8\pi cm/s\) và gia tốc cực đại \({a_{max}} = 16{\pi ^2}cm/{s^2}\) thì tần số của dao động là:
Đáp án : A Phương pháp giải :
Sử dụng công thức xác định gia tốc cực đại và vận tốc cực đại trong dao động điều hòa: \({v_{max}} = A\omega ,{\rm{ }}{a_{max}} = {\omega ^2}A\) Lời giải chi tiết :
Ta có: $\left\{ \begin{gathered}{v_{{\text{max}}}} = \omega A \hfill \\{a_{{\text{max}}}} ={\omega ^2}A \hfill \\\end{gathered} \right. \to \left[ {\dfrac{{{a_{{\text{max}}}}}}{{{v_{{\text{max}}}}}} = \dfrac{{{\omega ^2}A}}{{\omega A}} = \omega = \dfrac{{16{\pi ^2}}}{{8\pi }} = 2\pi = 2\pi f \to f = \dfrac{\omega }{{2\pi }}} \right. = 1H{\text{z}}$
Câu 26 :
Dao động điều hoà có vận tốc cực đại là \({v_{max}} = 16\pi cm/s\) và gia tốc cực đại \({a_{max}} = 64{\pi ^2}cm/{s^2}\) thì biên độ của dao động là:
Đáp án : C Phương pháp giải :
Sử dụng công thức xác định gia tốc cực đại và vận tốc cực đại trong dao động điều hòa: \({v_{max}} = A\omega ,{\rm{ }}{a_{max}} = {\omega ^2}A\) Lời giải chi tiết :
Ta có: $\left\{ \begin{gathered}{v_{{\text{max}}}} = \omega A \hfill \\{a_{{\text{max}}}} = {\omega ^2}A \hfill \\\end{gathered} \right. \to \dfrac{{{v^2}_{{\text{max}}}}}{{{a_{{\text{max}}}}}} = \dfrac{{{{(\omega A)}^2}}}{{{\omega ^2}A}} = A = \dfrac{{{{\left( {16\pi } \right)}^2}}}{{64\pi^2 }} = 4cm$
Câu 27 :
Một chất điểm dao động điều hoà với phương trình dạng\(x=cos(2\pi t + \dfrac{\pi}{6})(cm,s)\). Lấy \(\pi ^2 =10\), biểu thức gia tốc tức thời của chất điểm là:
Đáp án : C Phương pháp giải :
Sử dụng lí thuyết về phương trình gia tốc trong dao động điều hòa: $a = - {\omega ^2}Acos(\omega t + \varphi ) = {\omega ^2}Acos(\omega t + \varphi + \pi )$ Lời giải chi tiết :
Ta có: $a = - {\omega ^2}Acos(\omega t + \varphi ) = {\omega ^2}Acos(\omega t + \varphi + \pi )$ x = cos(2πt + π/6) (cm, s) $ \to a = - {(2\pi )^2}.1cos(2\pi t + \dfrac{\pi }{6}) = - 40cos(2\pi t + \dfrac{\pi }{6})$
Câu 28 :
Một vật thực hiện dao động điều hòa trên đoạn thẳng dài 12cm. Thời gian để vật đi được đoạn đường dài 24cm là 2s. Tốc độ của vật khi đi qua vị trí cân bằng là
Đáp án : B Phương pháp giải :
+ Chiều dài quỹ đạo: L = 2.A; trong đó A là biên độ dao động. + Quãng đường vật đi được trong 1 chu kì là 4A. + Tốc độ của vật khi qua VTCB: \({v_{\max }} = \omega A = \dfrac{{2\pi }}{T}.A\) Lời giải chi tiết :
Ta có: \(A = \dfrac{L}{2} = \dfrac{{12}}{2} = 6cm\) Vật đi được quãng đường \(S = 24cm = 4.A\) trong 2s \( \Rightarrow T = 2s\) → Tốc độ của vật khi qua vị trí cân bằng \({v_{ma{\rm{x}}}} = \omega A = 6\pi \,\,\left( {cm/s} \right)\)
Câu 29 :
Một điểm M chuyển động tròn đều trên một đường tròn với tốc độ 15 cm/s. Gọi P là hình chiếu của M lên một đường kính của đường tròn quỹ đạo. Tốc độ trung bình của P trong một dao động toàn phần bằng
Đáp án : B Phương pháp giải :
Tốc độ dài: \(v = \omega A\) Tốc độ trung bình: \(\overline v = \dfrac{S}{t}\) Lời giải chi tiết :
Tốc độ dài của chuyển động tròn đều: \({v_M} = 15\,\,cm/s = \omega R = \omega A = {v_{\max }} = {v_P}\) Tốc độ trung bình trong 1 chu kì: \(\overline v = \dfrac{S}{t} = \dfrac{{4A}}{T} = \dfrac{{4A\omega }}{{2\pi }} = \dfrac{{2A\omega }}{\pi }\) \( \Rightarrow \overline v = \dfrac{{2{v_{\max }}}}{\pi } = \dfrac{{2{v_p}}}{\pi } = \dfrac{{2.15}}{\pi } = 9,55\,\,\left( {cm/s} \right)\)
Câu 30 :
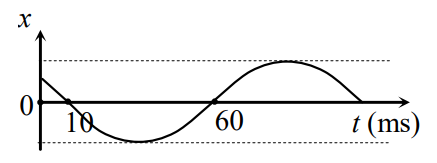
Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là
Đáp án : C Phương pháp giải :
Sử dụng kĩ năng đọc đồ thị Lời giải chi tiết :
Từ đồ thị ta thấy trong khoảng thời gian từ 10 ms đến 60 ms, vật thực hiện được \(\frac{1}{2}\) chu kì: \(\frac{T}{2} = 60 - 10 \Rightarrow T = 100\,\,\left( {ms} \right) = 0,1\,\,\left( s \right)\)
Câu 31 :
Đề thi thử THPT chuyên Lam Sơn - 2021 Một chất điểm dao động theo phương trình \(x = 6co{\rm{s}}\omega {\rm{t}}\left( {cm} \right)\). Dao động của chất điểm có biên độ là
Đáp án : B Phương pháp giải :
Phương trình dao động điều hòa: \(x = Aco{\rm{s}}\left( {\omega t + \varphi } \right)\), trong đó: + A: Biên độ dao động + \(\omega \): Tần số góc + \(\left( {\omega t + \varphi } \right)\): Pha dao động tại thời điểm t. Lời giải chi tiết :
Phương trình dao động: \(x = 6cos\omega t\left( {cm} \right)\) \( \Rightarrow \) Biên độ dao động \(A = 6cm\)
|



















Danh sách bình luận