Trắc nghiệm Bài 7. Phương trình sóng cơ học - Vật Lí 12Đề bài
Câu 1 :
Sóng truyền từ $O$ đến $M$ với vận tốc $v = 40cm/s$, phương trình sóng tại $O$ là \({u_0} = 4sin\dfrac{\pi }{2}t\left( {cm} \right)\). Biết vào thời điểm $t$ thì li độ của phần tử $M$ là $3cm$ và đang chuyển động theo chiều dương, vậy lúc $t + 6(s)$ li độ của $M$ là:
Câu 2 :
Một sóng cơ lan truyền trên một sợi dây rất dài có phương trình \(u = 6\cos \left( {4\pi t - 0,02\pi x} \right)\); trong đó u và x có đơn vị là cm, t có đơn vị là giây. Hãy xác định li độ dao động của một điểm trên dây có toạ độ x = 25 cm tại thời điểm t = 4 s.
Câu 3 :
Một sóng cơ học lan truyền trên mặt nước với tốc độ 25cm/s. Phương trình sóng tại nguồn là u = 3cosπt(cm). Vận tốc của phần tử vật chất tại điểm M cách O một khoảng 25cm tại thời điểm t = 2,5s là:
Câu 4 :
Nguồn sóng ở O dao động với tần số 10Hz, dao động truyền đi với vận tốc 0,4m/s theo phương Oy; trên phương này có hai điểm P và Q với PQ = 15cm. Biên độ sóng bằng a = 1cm và không thay đổi khi lan truyền . Nếu tại thời điểm t nào đó P có li độ 1cm thì li độ tại Q là:
Câu 5 :
Sóng có tần số \(20Hz\) truyền trên chất lỏng với tốc độ \(200cm/s\), gây ra các dao động theo phương thẳng đứng của các phần tử chất lỏng. Hai điểm M và N thuộc mặt chất lỏng cùng phương truyền sóng cách nhau \(22,5cm\). Biết điểm M nằm gần nguồn sóng hơn. Tại thời điểm t điểm N hạ xuống thấp nhất. Hỏi sau đó thời gian ngắn nhất là bao nhiêu thì điểm M sẽ hạ xuống thấp nhất?
Câu 6 :
Sóng truyền theo phương ngang trên một sợi dây dài với tần số $10Hz$. Điểm $M$ trên dây tại một thời điểm đang ở vị trí cao nhất và tại thời điểm đó điểm $N$ cách $M$ $5cm$ đang đi qua vị trí có li độ bằng nửa biên độ và đi lên. Coi biên độ sóng không đổi khi truyền. Biết khoảng cách $MN$ nhỏ hơn bước sóng của sóng trên dây. Chọn đáp án đúng cho tốc độ truyền sóng và chiều truyền sóng.
Câu 7 :
Hai điểm M, N cùng nằm trên một phương truyền sóng cách nhau λ/3. Tại thời điểm t, khi li độ dao động tại M là uM = + 3 cm thì li độ dao động tại N là uN = - 3 cm. Biên độ sóng bằng :
Câu 8 :
Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình sóng tại nguồn O là: \({u_O} = A\sin (\frac{{2\pi }}{T}t)(cm).\) Một điểm M cách nguồn O bằng \(\frac{1}{3}\) bước sóng ở thời điểm \(t = \frac{T}{2}\) có ly độ \({u_M} = 2(cm).\) Biên độ sóng A là:
Câu 9 :
Một sóng cơ lan truyền từ nguồn O, dọc theo trục Ox với biên độ sóng không đổi, chu kì sóng T và bước sóng \(\lambda \). Biết rằng tại thời điểm t = 0, phần tử tại O qua vị trí cân bằng theo chiều dương và tại thời điểm t = \(\frac{{5T}}{6}\) phần tử tại điểm M cách O một đoạn d = \(\frac{\lambda }{6}\) có li độ là -2 cm. Biên độ sóng là :
Câu 10 :
Trên một sợi dây dài vô hạn có một sóng cơ lan truyền theo phương Ox với phương trình sóng u = 2cos(10πt - πx) (cm) ( trong đó t tính bằng s; x tính bằng m). M, N là hai điểm nằm cùng phía so với O cách nhau 5 m. Tại cùng một thời điểm khi phần tử M đi qua vị trí cân bằng theo chiều dương thì phần tử N
Câu 11 :
Cho phương trình sóng: $u = a\sin \left( {0,4\pi x + 7\pi t + \dfrac{\pi }{3}} \right)\left( {m,s} \right)$. Phương trình này biểu diễn:
Câu 12 :
Một nguồn O dao động với tần số f = 50Hz tạo ra sóng trên mặt nước có biên độ 3cm (coi như không đổi khi sóng truyền đi). Chọn t = 0 là lúc phần tử nước tại O đi qua vị trí cân bằng theo chiều dương. Tại thời điểm t1 li độ dao động tại M bằng 2cm. Li độ dao động tại M vào thời điểm t2 = (t1 + 2,01)s bằng bao nhiêu ?
Câu 13 :
Một sóng cơ lan truyền trên một sợi dây rất dài với biên độ không đổi, ba điểm A, B và C nằm trên sợi dây sao cho B là trung điểm của AC. Tại thời điểm t1, li độ của ba phần tử A, B, C lần lượt là – 4,8mm; 0 mm; 4,8 mm. Nếu tại thời điểm t2, li độ của A và C đều bằng +5,5 mm, thì li độ của phần tử tại B là:
Câu 14 :
Một sợi dây đàn hồi nằm ngang có điểm đầu O dao động theo phương thẳng đứng với biên độ A = 5cm, T = 0,5s. Vận tốc truyền sóng là 40cm/s. Viết phương trình sóng tại M cách O d = 50 cm.
Câu 15 :
Một sóng cơ học truyền theo phương $Ox$ với biên độ coi như không đổi. Tại $O$, dao động có dạng $u = acosωt (cm)$. Điểm M cách xa tâm dao động O là \(\dfrac{1}{3}\) bước sóng ở thời điểm bằng $0,5$ chu kì thì ly độ sóng có giá trị là $5 cm$. Phương trình dao động ở M thỏa mãn hệ thức nào sau đây:
Câu 16 :
Một dao động lan truyền trong môi trường từ điểm $N$ đến điểm $M$ cách $N$ một đoạn $0,9 (m)$ với vận tốc $1,2 (m/s)$. Biết phương trình sóng tại $N$ có dạng $u_N = 0,02cos 2πt(m)$. Viết biểu thức sóng tại $M$ :
Câu 17 :
Một sóng cơ học lan truyền trên một phương truyền sóng với vận tốc $5m/s$. Phương trình sóng của một điểm O trên phương truyền đó là:\({u_O} = 6c{\rm{os}}\left( {5\pi t + \dfrac{\pi }{2}} \right)\). Phương trình sóng tại M nằm trước O và cách O một khoảng $50cm$ là:
Câu 18 :
Sóng truyền từ điểm M đến điểm O rồi đến điểm N trên cùng một phương truyền sóng với tốc độ \(v = 20m/s\). Cho biết tại O dao động có phương trình \({u_O} = 4cos\left( {2\pi f - \dfrac{\pi }{2}} \right)cm\) và tại hai điểm gần nhau nhất cách nhau \(6m\) trên cùng phương truyền sóng thì dao động lệch pha nhau góc \(\dfrac{{2\pi }}{3}rad\). Cho \(ON = 50cm\). Phương trình sóng tại N là
Câu 19 :
Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình dao động tại nguồn O là \({u_O} = A.\cos \left( {\dfrac{{2\pi t}}{T}} \right)cm\). Một điểm M trên đường thẳng, cách O một khoảng bằng \(\dfrac{1}{3}\) bước sóng ở thời điểm \(t = \dfrac{T}{2}\) có li độ uM = 2cm. Biên độ sóng A bằng:
Lời giải và đáp án
Câu 1 :
Sóng truyền từ $O$ đến $M$ với vận tốc $v = 40cm/s$, phương trình sóng tại $O$ là \({u_0} = 4sin\dfrac{\pi }{2}t\left( {cm} \right)\). Biết vào thời điểm $t$ thì li độ của phần tử $M$ là $3cm$ và đang chuyển động theo chiều dương, vậy lúc $t + 6(s)$ li độ của $M$ là:
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính góc quét: \(\Delta \varphi = \omega \Delta t\) + Sử dụng vòng tròn lượng giác Lời giải chi tiết :
Góc quét được: \(\Delta \varphi = \omega \Delta t = \dfrac{\pi }{2}6= {3\pi }\) Vẽ trên vòng tròn lượng giác, ta được: 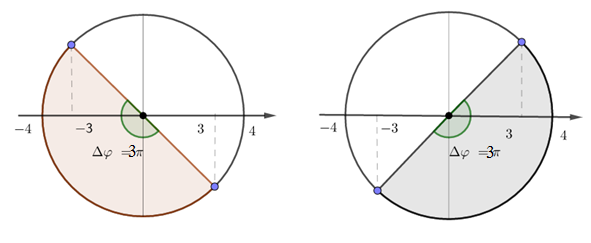 Từ vòng tròn lượng giác, ta có: $t + 6s$ điểm $M$ có li độ $-3cm$
Câu 2 :
Một sóng cơ lan truyền trên một sợi dây rất dài có phương trình \(u = 6\cos \left( {4\pi t - 0,02\pi x} \right)\); trong đó u và x có đơn vị là cm, t có đơn vị là giây. Hãy xác định li độ dao động của một điểm trên dây có toạ độ x = 25 cm tại thời điểm t = 4 s.
Đáp án : A Phương pháp giải :
Thay x và t vào phương trình dao động Lời giải chi tiết :
Ta có: \(u = 6\cos \left( {4\pi t - 0,02\pi x} \right)\) Thay x = 25cm và t = 4s vào, ta được: \(u = 6\cos \left( {4\pi .4 - 0,02\pi .25} \right) = 0cm\)
Câu 3 :
Một sóng cơ học lan truyền trên mặt nước với tốc độ 25cm/s. Phương trình sóng tại nguồn là u = 3cosπt(cm). Vận tốc của phần tử vật chất tại điểm M cách O một khoảng 25cm tại thời điểm t = 2,5s là:
Đáp án : B Phương pháp giải :
+ Áp dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\) + Viết phương trình li độ dao động tại M + Viết phương trình vận tốc tại M, thay t vào phương trình vận tốc Lời giải chi tiết :
Ta có: \(\lambda = \frac{v}{f} = \frac{{25}}{{\frac{\pi }{{2\pi }}}} = 50cm\) Phương trình dao động tại M cách O một khoảng x = 25cm: \({u_M} = 3c{\rm{os}}\left( {\pi t - \frac{{2\pi x}}{\lambda }} \right) = 3c{\rm{os}}\left( {\pi t - \frac{{2\pi 25}}{{50}}} \right) = 3c{\rm{os}}\left( {\pi t - \pi } \right)cm\) Phương trình vận tốc tại M: \({v_M} = {u_M}' = - 3\pi \sin \left( {\pi t - \pi } \right)cm/s\) => Vận tốc tại M tại thời điểm t = 2,5s: \({v_M} = - 3\pi \sin \left( {\pi .2,5 - \pi } \right) = 3\pi cm/s\)
Câu 4 :
Nguồn sóng ở O dao động với tần số 10Hz, dao động truyền đi với vận tốc 0,4m/s theo phương Oy; trên phương này có hai điểm P và Q với PQ = 15cm. Biên độ sóng bằng a = 1cm và không thay đổi khi lan truyền . Nếu tại thời điểm t nào đó P có li độ 1cm thì li độ tại Q là:
Đáp án : C Phương pháp giải :
+ Áp dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\) + Vận dụng công thức tính độ lệch pha: \(\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda }\) + Sử dụng vòng tròn lượng giác. Lời giải chi tiết :
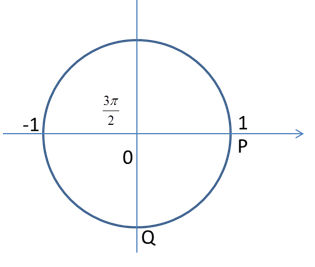 Ta có: \(\lambda = \frac{v}{f} = \frac{{0,4}}{{10}} = 0,04m = 4cm\) Độ lệch pha giữa hai điểm P và Q là: \(\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda } = \frac{{2\pi 15}}{4} = \frac{{15\pi }}{2} = 6\pi + \frac{{3\pi }}{2}\) Từ vòng tròn lượng giác, ta có li độ tại Q là 0cm
Câu 5 :
Sóng có tần số \(20Hz\) truyền trên chất lỏng với tốc độ \(200cm/s\), gây ra các dao động theo phương thẳng đứng của các phần tử chất lỏng. Hai điểm M và N thuộc mặt chất lỏng cùng phương truyền sóng cách nhau \(22,5cm\). Biết điểm M nằm gần nguồn sóng hơn. Tại thời điểm t điểm N hạ xuống thấp nhất. Hỏi sau đó thời gian ngắn nhất là bao nhiêu thì điểm M sẽ hạ xuống thấp nhất?
Đáp án : B Phương pháp giải :
+ Áp dụng công thức tính bước sóng: \(\lambda = \dfrac{v}{f}\) + Áp dụng công thức tính chu kì: \(T = \dfrac{1}{f} = 0,05{\rm{s}}\) + Vận dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda }\) + Sử dụng vòng tròn lượng giác. Lời giải chi tiết :
Ta có: \(\lambda = \dfrac{v}{f} = \dfrac{{200}}{{20}} = 10cm\) Chu kì: \(T = \dfrac{1}{f} = 0,05{\rm{s}}\) Độ lệch pha giữa hai điểm M và N là: \(\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{2\pi 22,5}}{{10}} = \dfrac{{9\pi }}{2} = 4\pi + \dfrac{\pi }{2}\) => M và N dao động vuông pha nhau Vì M gần nguồn sóng hơn => M nhanh pha hơn N 1 góc π/2 Tại thời điểm t: N đang ở biên âm, M đang ở VTCB theo chiều dương => Thời gian ngắn nhất điểm M hạ xuống thấp nhất là: \(t = \dfrac{{3T}}{4} = \dfrac{3}{{80}}s\) 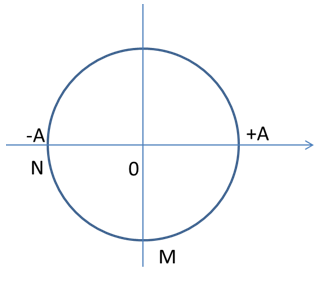
Câu 6 :
Sóng truyền theo phương ngang trên một sợi dây dài với tần số $10Hz$. Điểm $M$ trên dây tại một thời điểm đang ở vị trí cao nhất và tại thời điểm đó điểm $N$ cách $M$ $5cm$ đang đi qua vị trí có li độ bằng nửa biên độ và đi lên. Coi biên độ sóng không đổi khi truyền. Biết khoảng cách $MN$ nhỏ hơn bước sóng của sóng trên dây. Chọn đáp án đúng cho tốc độ truyền sóng và chiều truyền sóng.
Đáp án : C Phương pháp giải :
+ Sử dụng vòng tròn lượng giác. + Vận dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda }\) + Áp dụng công thức tính tốc độ truyền sóng: \(v = \lambda f\) Lời giải chi tiết :
Ta có: + Điểm $M$ ở vị trí cao nhất tức là biên dương. + Điểm $N$ qua vị trí có li độ bằng $\dfrac{A}{2}$ và đang đi lên Vẽ trên vòng tròn lượng giác, ta được: 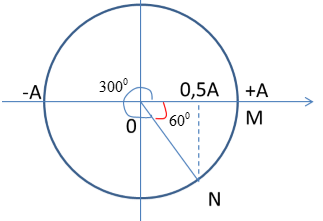 Ta có 2 trường hợp của góc lệch pha giữa $M$ và $N$: + TH 1: $M, N$ lệch pha nhau: $60^0$: \(\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{\pi }{3} \to \lambda = 6\Delta d = 6.5 = 30cm\\ \to v = \lambda f = 30.10 = 300cm/s = 3m/s\end{array}\) $M$ sớm pha hơn $N$ => Sóng truyền từ $M$ đến $N$ + TH 2: $M, N$ lệch pha nhau $300^0$: \(\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{5\pi }}{3} \to \lambda = \dfrac{6}{5}\Delta d = \dfrac{6}{5}.5 = 6cm\\ \to v = \lambda f = 6.10 = 60cm/s\end{array}\) Do $N$ sớm pha hơn $M$ => Sóng truyền từ $N$ đến $M$
Câu 7 :
Hai điểm M, N cùng nằm trên một phương truyền sóng cách nhau λ/3. Tại thời điểm t, khi li độ dao động tại M là uM = + 3 cm thì li độ dao động tại N là uN = - 3 cm. Biên độ sóng bằng :
Đáp án : C Phương pháp giải :
Áp dụng biểu thức xác định độ lệch pha: \(\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda }\) + Cách 1: Dùng phương trình sóng Viết phương trình sóng tại M và N Áp dụng công thức lượng giác: \({\rm{cosa + cosb}} = 2c{\rm{os}}\frac{{a + b}}{2}{\rm{cos}}\frac{{a - b}}{2}\) + Cách 2: Sử dụng vòng tròn lượng giác Lời giải chi tiết :
Ta có: Độ lệch pha giữa hai điểm MN là: \(\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda } = \frac{{2\pi \frac{\lambda }{3}}}{\lambda } = \frac{{2\pi }}{3}\) Giả sử dao động tại M sớm pha hơn dao động tại N. Cách 1: Dùng phương trình sóng Ta có thể viết: \(\begin{array}{l}{u_M} = Ac{\rm{os}}\omega t = + 3cm{\rm{ (1)}}\\{u_N} = Ac{\rm{os}}\left( {\omega t - \frac{{2\pi }}{3}} \right) = - 3cm{\rm{ (2)}}\end{array}\) Lấy (1) + (2), ta được: \(\begin{array}{l}{u_M} + {u_N} = 0 = Ac{\rm{os}}\omega t + Ac{\rm{os}}\left( {\omega t - \frac{{2\pi }}{3}} \right)\\ \leftrightarrow 2Ac{\rm{os}}\frac{\pi }{3}{\rm{cos}}\left( {\omega t - \frac{\pi }{3}} \right) = 0 \to \omega t - \frac{\pi }{3} = \frac{\pi }{2} + k\pi \\ \to \omega t = \frac{{5\pi }}{6} + k\pi \end{array}\) Thay vào (1), ta được: \(Ac{\rm{os}}\left( {\frac{{5\pi }}{6} + k\pi } \right) = 3\) Do A > 0, \(Ac{\rm{os}}\left( {\frac{{5\pi }}{6} - \pi } \right) = 3 \to Ac{\rm{os}}\left( { - \frac{\pi }{6}} \right) = 3 \to A = 2\sqrt 3 cm\) => Chọn C Cách 2: Sử dụng vòng tròn lượng giác Xác định tọa độ N, M trên vòng tròn lượng giác, ta được: Từ vòng tròn lượng giác, ta có: \(\begin{array}{l}\angle NOK = \angle KOM = \frac{{\Delta \varphi }}{2} = \frac{\pi }{3}\\ \to {\rm{A}}\sin \frac{\pi }{3} = 3cm \to A = 2\sqrt 3 cm\end{array}\) 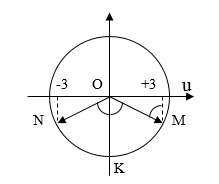
Câu 8 :
Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình sóng tại nguồn O là: \({u_O} = A\sin (\frac{{2\pi }}{T}t)(cm).\) Một điểm M cách nguồn O bằng \(\frac{1}{3}\) bước sóng ở thời điểm \(t = \frac{T}{2}\) có ly độ \({u_M} = 2(cm).\) Biên độ sóng A là:
Đáp án : A Phương pháp giải :
Áp dụng biểu thức xác định độ lệch pha: \(\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda }\) + Viết phương trình sóng tại M + Thay x và t vào phương trình sóng Lời giải chi tiết :
Ta có: \({u_O} = A\sin (\frac{{2\pi }}{T}t)(cm) \to {u_M}{\rm{ = Asin}}\left( {\frac{{2\pi }}{T}t - \frac{{2\pi x}}{\lambda }} \right)\) Thay t = T/2 và x = λ/3 vào phương trình dao động tại M, ta được: \(\begin{array}{l}{u_M}{\rm{ = Asin}}\left( {\frac{{2\pi }}{T}t - \frac{{2\pi x}}{\lambda }} \right) \leftrightarrow {\rm{Asin}}\left( {\frac{{2\pi }}{T}\frac{T}{2} - \frac{{2\pi \frac{\lambda }{3}}}{\lambda }} \right) = 2\\ \to A\sin \left( {\frac{\pi }{3}} \right) = 2 \to A = \frac{4}{{\sqrt 3 }}cm\end{array}\)
Câu 9 :
Một sóng cơ lan truyền từ nguồn O, dọc theo trục Ox với biên độ sóng không đổi, chu kì sóng T và bước sóng \(\lambda \). Biết rằng tại thời điểm t = 0, phần tử tại O qua vị trí cân bằng theo chiều dương và tại thời điểm t = \(\frac{{5T}}{6}\) phần tử tại điểm M cách O một đoạn d = \(\frac{\lambda }{6}\) có li độ là -2 cm. Biên độ sóng là :
Đáp án : A Phương pháp giải :
+ Viết phương trình sóng tại O + Viết phương trình sóng tại M + Thay x và t vào phương trình sóng Lời giải chi tiết :
Ta có: - Phương trình sóng tại O: \({u_0} = Ac{\rm{os}}\left( {\omega t - \frac{\pi }{2}} \right)cm\) - Phương trình sóng tại M: \({u_M} = Ac{\rm{os}}\left( {\omega t - \frac{\pi }{2} - \frac{{2\pi d}}{\lambda }} \right)cm\) Tại t = 5T/6 và d = λ/6 \(\begin{array}{l}{u_M} = Ac{\rm{os}}\left( {\frac{{2\pi }}{T}\frac{{5T}}{6} - \frac{\pi }{2} - \frac{{2\pi \frac{\lambda }{6}}}{\lambda }} \right) = - 2cm\\ \to Ac{\rm{os}}\left( {\frac{{5\pi }}{6}} \right) = - 2 \to A = \frac{4}{{\sqrt 3 }}cm\end{array}\)
Câu 10 :
Trên một sợi dây dài vô hạn có một sóng cơ lan truyền theo phương Ox với phương trình sóng u = 2cos(10πt - πx) (cm) ( trong đó t tính bằng s; x tính bằng m). M, N là hai điểm nằm cùng phía so với O cách nhau 5 m. Tại cùng một thời điểm khi phần tử M đi qua vị trí cân bằng theo chiều dương thì phần tử N
Đáp án : B Phương pháp giải :
+ Vận dụng biểu thức tính độ lệch pha: \(\Delta \varphi = \frac{{2\pi x}}{\lambda }\) Lời giải chi tiết :
Từ phương trình sóng, ta có: \(\frac{{2\pi x}}{\lambda } = \pi x \to \lambda = 2m\) Độ lệch pha giữa 2 điểm M, N là: \(\Delta \varphi = \frac{{2\pi x}}{\lambda } = \frac{{2\pi .5}}{2} = 5\pi \) => M và N dao động ngược pha nhau => Khi M đi qua vị trí cân bằng theo chiều dương thì N đi qua vị trí cân bằng theo chiều âm
Câu 11 :
Cho phương trình sóng: $u = a\sin \left( {0,4\pi x + 7\pi t + \dfrac{\pi }{3}} \right)\left( {m,s} \right)$. Phương trình này biểu diễn:
Đáp án : D Phương pháp giải :
+ Đọc các đại lượng trong phương trình dao động sóng + Áp dụng công thức: \(\dfrac{{2\pi x}}{\lambda } = 0,4\pi x \to \lambda = \dfrac{2}{{0,4}} = 5m\) + Áp dụng công thức tính vận tốc truyền sóng: \(v = \lambda f\) Lời giải chi tiết :
Ta có: \(u = {\rm{a}}\sin \left( {7\pi t + 0,4\pi x + \dfrac{\pi }{3}} \right)(m,s)\) Ta thấy $"+0,4{\pi}x"$ => Sóng chạy theo chiều âm của trục x \(\dfrac{{2\pi x}}{\lambda } = 0,4\pi x \to \lambda = \dfrac{2}{{0,4}} = 5m\) Vận tốc truyền sóng: \(v = \lambda f = \lambda \dfrac{\omega }{{2\pi }} = 5.\dfrac{{7\pi }}{{2\pi }} = 17,5m/s\)
Câu 12 :
Một nguồn O dao động với tần số f = 50Hz tạo ra sóng trên mặt nước có biên độ 3cm (coi như không đổi khi sóng truyền đi). Chọn t = 0 là lúc phần tử nước tại O đi qua vị trí cân bằng theo chiều dương. Tại thời điểm t1 li độ dao động tại M bằng 2cm. Li độ dao động tại M vào thời điểm t2 = (t1 + 2,01)s bằng bao nhiêu ?
Đáp án : B Phương pháp giải :
+ Áp dụng công thức tính tần số góc: \(\omega = 2\pi f\) + Vận dụng công thức tính góc quyét trong thời gian ∆t: \(\Delta \varphi = \omega \Delta t\) + Sử dụng vòng tròn lượng giác Lời giải chi tiết :
Tần số góc: \(\omega = 2\pi f = 2\pi .50 = 100\pi \left( {ra{\rm{d}}/s} \right)\) Góc quyét của M từ t1 đến t2 là: \(\Delta \varphi = \omega \Delta t = 100\pi .2,01 = 201\pi \) => li độ của M tại t1 và t2 ngược pha nhau => tại t2 M có li độ là -2cm 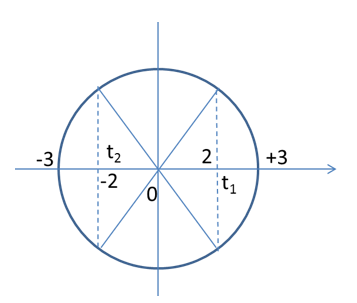
Câu 13 :
Một sóng cơ lan truyền trên một sợi dây rất dài với biên độ không đổi, ba điểm A, B và C nằm trên sợi dây sao cho B là trung điểm của AC. Tại thời điểm t1, li độ của ba phần tử A, B, C lần lượt là – 4,8mm; 0 mm; 4,8 mm. Nếu tại thời điểm t2, li độ của A và C đều bằng +5,5 mm, thì li độ của phần tử tại B là:
Đáp án : D Phương pháp giải :
+ Sử dụng vòng tròn lượng giác + Sử dụng hệ thức \({\sin ^2}\alpha + c{\rm{o}}{{\rm{s}}^2}\alpha = 1\) Lời giải chi tiết :
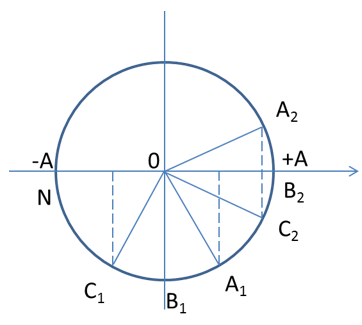 Xác định tọa độ các điểm tại các thời điểm t1 và t2 Từ vòng tròn lượng giác, ta có: B quay góc 900 => Tại t2 li độ B chính bằng biên độ A, C cũng tương tự Ta có: \(\frac{{4,{8^2}}}{{{A^2}}} + \frac{{5,{5^2}}}{{{A^2}}} = 1 \to A = \sqrt {4,{8^2} + 5,{5^2}} = 7,3mm\)
Câu 14 :
Một sợi dây đàn hồi nằm ngang có điểm đầu O dao động theo phương thẳng đứng với biên độ A = 5cm, T = 0,5s. Vận tốc truyền sóng là 40cm/s. Viết phương trình sóng tại M cách O d = 50 cm.
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính bước sóng: \(\lambda = vT\) + Áp dụng công thức tính tần số góc: \(\omega = \frac{{2\pi }}{T}\) + Viết phương trình dao động của một điểm Lời giải chi tiết :
Bước sóng: \(\lambda = vT = 40.0,5 = 20cm\) Tần số góc: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,5}} = 4\pi ra{\rm{d}}/s\) PT sóng tại M: \({u_M} = 5c{\rm{os}}\left( {4\pi t - \frac{{2\pi d}}{\lambda }} \right) = 5c{\rm{os}}\left( {4\pi t - \frac{{2\pi .50}}{{20}}} \right) = 5c{\rm{os}}\left( {4\pi t - 5\pi } \right)\)
Câu 15 :
Một sóng cơ học truyền theo phương $Ox$ với biên độ coi như không đổi. Tại $O$, dao động có dạng $u = acosωt (cm)$. Điểm M cách xa tâm dao động O là \(\dfrac{1}{3}\) bước sóng ở thời điểm bằng $0,5$ chu kì thì ly độ sóng có giá trị là $5 cm$. Phương trình dao động ở M thỏa mãn hệ thức nào sau đây:
Đáp án : C Lời giải chi tiết :
PT sóng tại O: \(u = ac{\rm{os}}\omega {\rm{t}}\left( {cm} \right)\) PT sóng tại M: \({u_M} = ac{\rm{os}}\left( {\omega t \pm \frac{{2\pi d}}{\lambda }} \right) = ac{\rm{os}}\left( {\omega t \pm \frac{{2\pi \frac{\lambda }{3}}}{\lambda }} \right) = ac{\rm{os}}\left( {\omega t \pm \frac{{2\pi }}{3}} \right)\) Tại thời điểm t = 0,5T thì u = 5cm \(\begin{array}{l}{u_M} = ac{\rm{os}}\left( {\omega \frac{T}{2} \pm \frac{{2\pi }}{3}} \right) = ac{\rm{os}}\left( {\frac{{2\pi }}{T}.\frac{T}{2} \pm \frac{{2\pi }}{3}} \right)\\ = ac{\rm{os}}\left( {\frac{{2\pi }}{T}.\frac{T}{2} \pm \frac{{2\pi }}{3}} \right) = 5cm\\ \leftrightarrow ac{\rm{os}}\left( {\pi \pm \frac{{2\pi }}{3}} \right) = 5cm \to a = 10cm\end{array}\) => Phương trình sóng tại M: \({u_M} = 10\cos (\omega t - \frac{{2\pi }}{3})cm\)
Câu 16 :
Một dao động lan truyền trong môi trường từ điểm $N$ đến điểm $M$ cách $N$ một đoạn $0,9 (m)$ với vận tốc $1,2 (m/s)$. Biết phương trình sóng tại $N$ có dạng $u_N = 0,02cos 2πt(m)$. Viết biểu thức sóng tại $M$ :
Đáp án : C Phương pháp giải :
+ Áp dụng biểu thức tính bước sóng: \(\lambda = vT\) + Viết phương trình dao động của một điểm Lời giải chi tiết :
Bước sóng: \(\lambda = vT = v\dfrac{{2\pi }}{\omega } = 1,2\dfrac{{2\pi }}{{2\pi }} = 1,2m\) Sóng truyền từ N đến M, ta có phương trình sóng tại M là: \({u_M} = 0,02c{\rm{os}}\left( {2\pi t - \dfrac{{2\pi d}}{\lambda }} \right) = 0,02c{\rm{os}}\left( {2\pi t - \dfrac{{2\pi 0,9}}{{1,2}}} \right) = 0,02c{\rm{os}}\left( {2\pi t - \dfrac{{3\pi }}{2}} \right)m\)
Câu 17 :
Một sóng cơ học lan truyền trên một phương truyền sóng với vận tốc $5m/s$. Phương trình sóng của một điểm O trên phương truyền đó là:\({u_O} = 6c{\rm{os}}\left( {5\pi t + \dfrac{\pi }{2}} \right)\). Phương trình sóng tại M nằm trước O và cách O một khoảng $50cm$ là:
Đáp án : D Phương pháp giải :
+ Áp dụng biểu thức tính bước sóng: \(\lambda = vT\) + Viết phương trình dao động của một điểm Lời giải chi tiết :
Bước sóng: \(\lambda = vT = v\frac{{2\pi }}{\omega } = 5\frac{{2\pi }}{{5\pi }} = 2m\) Do M nằm trước O, ta có phương trình dao động của M là: \({u_M} = 6c{\rm{os}}\left( {5\pi t + \frac{\pi }{2} + \frac{{2\pi d}}{\lambda }} \right) = 6c{\rm{os}}\left( {5\pi t + \frac{\pi }{2} + \frac{{2\pi 0,5}}{2}} \right) = 6c{\rm{os}}\left( {5\pi t + \pi } \right)\)
Câu 18 :
Sóng truyền từ điểm M đến điểm O rồi đến điểm N trên cùng một phương truyền sóng với tốc độ \(v = 20m/s\). Cho biết tại O dao động có phương trình \({u_O} = 4cos\left( {2\pi f - \dfrac{\pi }{2}} \right)cm\) và tại hai điểm gần nhau nhất cách nhau \(6m\) trên cùng phương truyền sóng thì dao động lệch pha nhau góc \(\dfrac{{2\pi }}{3}rad\). Cho \(ON = 50cm\). Phương trình sóng tại N là
Đáp án : C Phương pháp giải :
+ Sử dụng biểu thức tính độ lệch pha: $\Delta \varphi = \dfrac{{2\pi d}}{\lambda }$ + Sử dụng biểu thức: $\lambda = \dfrac{v}{f}$ Lời giải chi tiết :
+ Độ lệch pha giữa hai điểm gần nhau nhất cách nhau \(6m\) trên phương truyền sóng dao động lệch pha nhau \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi }}{3}\) \( \Rightarrow \lambda = \dfrac{{2\pi .6}}{{\dfrac{{2\pi }}{3}}} = 18m\) Lại có: \(\lambda = \dfrac{v}{f} \Rightarrow f = \dfrac{v}{\lambda } = \dfrac{{20}}{{18}} = \dfrac{{10}}{9}Hz\) \( \Rightarrow \omega = 2\pi f = \dfrac{{20\pi }}{9}\left( {rad/s} \right)\) + Phương trình sóng tại N: \({u_N} = 4cos\left( {\dfrac{{20\pi }}{9}t - \dfrac{\pi }{2} - \dfrac{{2\pi .ON}}{\lambda }} \right) = 4\cos \left( {\dfrac{{20\pi }}{9}t - \dfrac{{5\pi }}{9}} \right)cm\)
Câu 19 :
Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình dao động tại nguồn O là \({u_O} = A.\cos \left( {\dfrac{{2\pi t}}{T}} \right)cm\). Một điểm M trên đường thẳng, cách O một khoảng bằng \(\dfrac{1}{3}\) bước sóng ở thời điểm \(t = \dfrac{T}{2}\) có li độ uM = 2cm. Biên độ sóng A bằng:
Đáp án : C Phương pháp giải :
Phương trình sóng tại nguồn: \({u_O} = A.\cos \left( {\dfrac{{2\pi t}}{T}} \right)cm\) Phương trình sóng tại M cách O một khoảng x: \({u_M} = A.\cos \left( {\dfrac{{2\pi t}}{T} - \dfrac{{2\pi .x}}{\lambda }} \right)cm\) Thay \(t = \dfrac{T}{2}\) vào phương trình của uM suy ra được A Lời giải chi tiết :
Phương trình sóng tại M cách O một khoảng \(\dfrac{1}{3}\) bước sóng là: \({u_M} = A.\cos \left( {\dfrac{{2\pi t}}{T} - \dfrac{{2\pi .\dfrac{\lambda }{3}}}{\lambda }} \right) = A.\cos \left( {\dfrac{{2\pi t}}{T} - \dfrac{{2\pi }}{3}} \right)cm\) Tại \(t = \dfrac{T}{2}\) li độ uM = 2cm. Ta có: \({u_M} = 2 \Leftrightarrow A.\cos \left( {\dfrac{{2\pi .\dfrac{T}{2}}}{T} - \dfrac{{2\pi }}{3}} \right) = 2cm \Rightarrow A = \dfrac{2}{{\cos \dfrac{\pi }{3}}} = 4cm\)
|



















Danh sách bình luận