Trắc nghiệm Bài 2. Năng lượng của con lắc lò xo - Vật Lí 12Đề bài
Câu 1 :
Biểu thức nào sau đây xác định cơ năng của con lắc lò xo dao động điều hòa?
Câu 2 :
Cơ năng của một con lắc lò xo tỉ lệ thuận với:
Câu 3 :
Trong dao động điều hòa, vì cơ năng được bảo toàn nên
Câu 4 :
Cơ năng của một con lắc lò xo không phụ thuộc vào?
Câu 5 :
Một con lắc lò xo dao động điều hoà với biên độ A. Khi tăng độ cứng của lò xo lên 4 lần và giảm biên độ dao động 2 lần thì cơ năng của con lắc sẽ:
Câu 6 :
Một chất điểm khối lượng $m = 100 (g)$, dao động điều hoà với phương trình $x = 4cos(2t) cm$. Cơ năng trong dao động điều hoà của chất điểm là:
Câu 7 :
Một con lắc lò xo có độ cứng $k = 150 N/m$ và có năng lượng dao động là $E = 0,12 J$. Biên độ dao động của con lắc có giá trị là:
Câu 8 :
Một con lắc lò xo dao động điều hòa. Phát biểu nào sau đây là sai?
Câu 9 :
Chọn phát biểu sai về sự biến đổi năng lượng của một chất điểm dao động điều hòa với chu kỳ T, tần số f ?
Câu 10 :
Một con lắc lò xo dao động điều hòa và vật đang chuyển động từ vị trí biên về vị trí cân bằng thì:
Câu 11 :
Một vật có khối lượng $m = 200 (g)$, dao động điều hoà với phương trình $x=10cos(5\pi t)cm$ . Tại thời điểm $t=0,5(s)$ thì vật có động năng là:
Câu 12 :
Một con lắc lò xo dao động điều hòa với biên độ $A$, tần số góc $ω$. Li độ và vận tốc của vật khi $W_d=nW_t$ là:
Câu 13 :
Một vật dao động điều hòa với phương trình $x=10cos(4\pi t)cm$ . Tại thời điểm mà động năng bằng $3$ lần thế năng thì vật ở cách VTCB một khoảng:
Câu 14 :
Một vật dao động điều hòa với phương trình $x=10cos(4\pi t + \pi /3)cm$ . Tại thời điểm mà thế năng bằng $3$ lần động năng thì vật có tốc độ là:
Câu 15 :
Một vật dao động điều hòa với tần số góc $ω$, khi thế năng bằng $3$ lần động năng thì li độ $x$ và vận tốc $v$ của vật có mối liên hệ với nhau như thế nào?
Câu 16 :
Một lò xo có độ cứng k treo thẳng đứng vào điểm cố định, đầu dưới có vật $m = 100 (g)$. Vật dao động điều hòa với tần số $f = 5 Hz$, cơ năng là $W=0,08J$ . Lấy $g = 10 m/s^2$, \({\pi ^2} = 10\). Tỉ số động năng và thế năng tại li độ $x = 2 cm$ là:
Câu 17 :
Ở một thời điểm, vận tốc của một vật dao động điều hòa bằng 20% vận tốc cực đại, tỉ số giữa động năng và thế năng của vật là:
Câu 18 :
Một vật dao động điều hòa với chu kỳ T và biên độ là A. Khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là?
Câu 19 :
Một vật dao động điều hòa với chu kỳ T và biên độ là A. Ban đầu vật ở vị trí cân bằng, khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà động năng bằng thế năng là:
Câu 20 :
Con lắc lò xo dao động theo phương ngang với phương trình \(x = Acos(\omega t + \varphi )\). Cứ sau những khoảng thời gian bằng nhau và bằng \(\dfrac{\pi }{{40}}\left( s \right)\) thì động năng của vật bằng thế năng của lò xo. Con lắc dao động điều hoà với tần số góc:
Câu 21 :
Một chất điểm có khối lượng m = 1 kg dao động điều hoà với chu kì T = π/5 (s). Biết năng lượng của nó là 0,02 J. Biên độ dao động của chất điểm là:
Câu 22 :
Một chất điểm dao động điều hòa theo phương trình x = Acos(4πt – π/6) cm. Trong một giây đầu tiên từ thời điểm t = 0, chất điểm qua li độ mà động năng bằng thế năng bao nhiêu lần?
Câu 23 :
Một con lắc lò xo có m = 100 (g) dao động điều hoà với cơ năng W = 2 mJ và gia tốc cực đại amax = 80 cm/s2. Biên độ và tần số góc của dao động là:
Câu 24 :
Một con lắc lò xo dao động điều hòa gồm vật nặng có khối lượng \(m = 100g\) , đồ thị thế năng theo thời gian của con lăc như hình vẽ. Biết \({t_2} - {t_1} = 0,05s\), lấy \({\pi ^2} = 10\) . Biên độ và chu kì dao động của con lắc là: 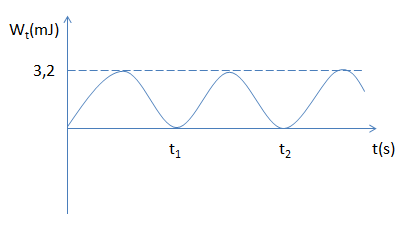
Câu 25 :
Một vật có khối lượng $400g$ dao động điều hòa có đồ thị động năng như hình vẽ. Tại thời điểm $t = 0$ vật đang chuyển động theo chiều dương, lấy $\pi^2=10$. Phương trình dao động của vật là: 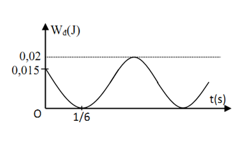
Câu 26 :
Con lắc lò xo dao động điều hòa trên mặt phẳng ngang không ma sát. Khi vật ở vị trí biên, ta giữ chặt một phần của lò xo làm cơ năng của vật giảm \(10\% \) thì biên độ dao động của hệ vật sẽ
Câu 27 :
Một vật nặng gắn vào một lò xo nhẹ có độ cứng k = 20 N/m thực hiện dao động điều hoà với biên độ A = 5cm. Động năng của vật khi nó cách vị trí cân bằng 4 cm là
Câu 28 :
Một con lắc lò xo có độ cứng \(k\), khối lượng vật nhỏ \(m\) dao động điều hoà. Tại thời điểm mà li độ và vận tốc của vật tương ứng là \(x\) và \(v\) thì động năng của vật là
Câu 29 :
Xét một con lắc lò xo gồm vật nhỏ và lò xo nhẹ dao động điều hòa trên mặt phẳng nằm ngang với biên độ A. Chọn gốc thế năng tại vị trí cân bằng. Tại vị trí con lắc có động năng bằng cơ năng, li độ của vật có giá trị là:
Câu 30 :
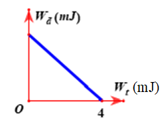
Động năng dao động của một con lắc lò xo được mô tả theo thế năng dao động của nó bằng đồ thị như hình vẽ. Cho biết khối lượng của vật bằng \(100\,\,g\), vật dao động giữa hai vị trí cách nhau \(8\,\,cm\). Tần số góc của dao động
Lời giải và đáp án
Câu 1 :
Biểu thức nào sau đây xác định cơ năng của con lắc lò xo dao động điều hòa?
Đáp án : D Lời giải chi tiết :
Cơ năng của con lắc lò xo dao động điều hòa: \(W = \dfrac{1}{2}k{A^2}\)
Câu 2 :
Cơ năng của một con lắc lò xo tỉ lệ thuận với:
Đáp án : C Phương pháp giải :
Vận dụng biểu thức cơ năng của con lắc lò xo dao động điều hòa: \(W = \dfrac{1}{2}k{A^2}\) Lời giải chi tiết :
Ta có, cơ năng của con lắc lò xo dao động điều hòa: \(W = \dfrac{1}{2}k{A^2}\) => Cơ năng thỉ lệ thuận với độ cứng k và bình phương biên độ dao động
Câu 3 :
Trong dao động điều hòa, vì cơ năng được bảo toàn nên
Đáp án : C Phương pháp giải :
Vận dụng lí thuyết và biểu thức cơ năng Lời giải chi tiết :
Ta có, Cơ năng bằng tổng động năng và thế năng mà cơ năng bảo toàn => Động năng tăng bao nhiêu thì thế năng giảm bấy nhiêu và ngược lại.
Câu 4 :
Cơ năng của một con lắc lò xo không phụ thuộc vào?
Đáp án : A Phương pháp giải :
Vận dụng biểu thức cơ năng của con lắc lò xo: \(W = \dfrac{1}{2}k{A^2}\) Lời giải chi tiết :
Ta có, cơ năng của con lắc lò xo \(W = \dfrac{1}{2}k{A^2}\) => Cơ năng của con lắc phụ thuộc vào độ cứng, biên độ dao động của vật
Câu 5 :
Một con lắc lò xo dao động điều hoà với biên độ A. Khi tăng độ cứng của lò xo lên 4 lần và giảm biên độ dao động 2 lần thì cơ năng của con lắc sẽ:
Đáp án : A Phương pháp giải :
Vận dụng biểu thức cơ năng của con lắc lò xo: \(W = \dfrac{1}{2}k{A^2}\) Lời giải chi tiết :
Ta có, cơ năng của con lắc lò xo: \(W = \dfrac{1}{2}k{A^2}\) => Khi tăng độ cứng của lò xo lên 4 lần và giảm biên độ dao động 2 lần thì cơ năng của con lắc vẫn không thay đổi
Câu 6 :
Một chất điểm khối lượng $m = 100 (g)$, dao động điều hoà với phương trình $x = 4cos(2t) cm$. Cơ năng trong dao động điều hoà của chất điểm là:
Đáp án : D Phương pháp giải :
+ Đọc phương trình dao động điều hòa + Áp dụng biểu thức xác định cơ năng của dao động điều hòa: \(W = \dfrac{1}{2}m{\omega ^2}{A^2}\) Lời giải chi tiết :
Từ phương trình dao động điều hòa, ta có biên độ $A = 4cm$, tần số góc $\omega = 2$ Cơ năng trong dao động điều hòa của chất điểm: \(W = \dfrac{1}{2}m{\omega ^2}{A^2} = \dfrac{1}{2}0,{1.2^2}.0,{04^2} = 3,{2.10^{ - 4}}J\)
Câu 7 :
Một con lắc lò xo có độ cứng $k = 150 N/m$ và có năng lượng dao động là $E = 0,12 J$. Biên độ dao động của con lắc có giá trị là:
Đáp án : C Phương pháp giải :
Áp dụng biểu thức cơ năng của con lắc lò xo: \(W = \dfrac{1}{2}k{A^2}\) Lời giải chi tiết :
Cơ năng dao động của con lắc lò xo: \(W = \dfrac{1}{2}k{A^2} \to A = \sqrt {\dfrac{{2{\rm{W}}}}{k}} = \sqrt {\dfrac{{2.0,12}}{{150}}} = 0,04m = 4cm\)
Câu 8 :
Một con lắc lò xo dao động điều hòa. Phát biểu nào sau đây là sai?
Đáp án : A Lời giải chi tiết :
A - sai vì: Động năng của con lắc lò xo: \(\begin{array}{l}{W_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}(\omega t + \varphi )\\ = W - {W_t} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}k{x^2}\end{array}\) B, C, D - đúng
Câu 9 :
Chọn phát biểu sai về sự biến đổi năng lượng của một chất điểm dao động điều hòa với chu kỳ T, tần số f ?
Đáp án : C Lời giải chi tiết :
Động năng và thế năng của vật biến thiên điều hòa với cùng tần số góc 2𝜔, tần số 2f và chu kì T/2. Cơ năng được bảo toàn => C - sai
Câu 10 :
Một con lắc lò xo dao động điều hòa và vật đang chuyển động từ vị trí biên về vị trí cân bằng thì:
Đáp án : A Phương pháp giải :
Vận dụng lí thuyết về dao động điều hòa và năng lượng của con lắc lò xo Lời giải chi tiết :
Khi vật đang chuyển động từ vị trí biên về vị trí cân bằng thì: Thế năng giảm - Động năng tăng - Cơ năng bảo toàn.
Câu 11 :
Một vật có khối lượng $m = 200 (g)$, dao động điều hoà với phương trình $x=10cos(5\pi t)cm$ . Tại thời điểm $t=0,5(s)$ thì vật có động năng là:
Đáp án : B Phương pháp giải :
+ Cách 1: Từ phương trình li độ, viết phương trình vận tốc, thay t vào phương trình vận tốc suy ra v Áp dụng biểu thức tính động năng của con lắc lò xo: \(W = \frac{1}{2}m{v^2}\) + Cách 2: Thay t vào phương trình li độ, từ x dùng hệ thức độc lập A - x - v suy ra vận tốc: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\) Áp dụng biểu thức tính động năng của con lắc lò xo: \(W = \frac{1}{2}m{v^2}\) Lời giải chi tiết :
Cách 1: Phương trình vận tốc của vật: v = x’(t) = -50psin(5pt) cm/s (1) Tại t = 0,5s thay vào (1) => v = -50p => Động năng của vật: \({{\text{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.0,2.{(0,5\pi )^2} = 0,25J\) Cách 2: Thay t = 0,5s vào phương trình dao động, ta có: x = 0 => vmax => Động năng của vật khi đó chính bằng cơ năng: \({{\text{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,2.{(5\pi .0,1)^2} = 0,25J\) Chú ý
Có thể dùng hệ thức độc lập để xác định vận tốc v: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\)
Câu 12 :
Một con lắc lò xo dao động điều hòa với biên độ $A$, tần số góc $ω$. Li độ và vận tốc của vật khi $W_d=nW_t$ là:
Đáp án : C Phương pháp giải :
Xem lí thuyết phần biết động năng tại vị trí có li độ x gấp n lần thế năng của vật: Wđ = nWt Lời giải chi tiết :
Tại vị trí có động năng gấp n lần thế năng của vật: Wđ = nWt \(\left\{ \begin{array}{l}{W_d} = n{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{1}{{n + 1}}W\\{W_d} = \dfrac{n}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm \dfrac{A}{{\sqrt {n + 1} }}\\v = \pm A\omega \sqrt {\dfrac{n}{{n + 1}}} \end{array} \right.\)
Câu 13 :
Một vật dao động điều hòa với phương trình $x=10cos(4\pi t)cm$ . Tại thời điểm mà động năng bằng $3$ lần thế năng thì vật ở cách VTCB một khoảng:
Đáp án : B Phương pháp giải :
+ Đọc phương trình dao động điều hòa + Áp dụng biểu thức xác định li độ dao động của vật khi biết Wđ = nWt : \(\left\{ \begin{array}{l}{W_d} = n{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to {W_t} = \dfrac{1}{{n + 1}}W \to x = \pm \dfrac{A}{{\sqrt {n + 1} }}\) Lời giải chi tiết :
Từ phương trình dao động điều hòa, ta có: Biên độ dao động A = 10cm Khi Wđ = 3Wt \(\left\{ \begin{array}{l}{W_d} = 3{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to {W_t} = \dfrac{1}{{3 + 1}}W \to x = \pm \dfrac{A}{{\sqrt {3 + 1} }} = \pm 5cm\)
Câu 14 :
Một vật dao động điều hòa với phương trình $x=10cos(4\pi t + \pi /3)cm$ . Tại thời điểm mà thế năng bằng $3$ lần động năng thì vật có tốc độ là:
Đáp án : B Phương pháp giải :
+ Đọc phương trình dao động điều hòa + Áp dụng biểu thức xác định vận tốc của vật khi biết Wt = nWđ : \(\left\{ \begin{array}{l}{W_t} = n{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to {W_d} = \dfrac{1}{{n + 1}}W \to v = \pm \dfrac{{A\omega }}{{\sqrt {n + 1} }}\) Lời giải chi tiết :
Từ phương trình dao động điều hòa, ta có: + Biên độ A = 10 cm + Tần số góc: ω = 4p Khi Wđ = 3Wt \(\left\{ \begin{array}{l}{W_t} = 3{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to {W_d} = \dfrac{1}{{3 + 1}}W \to v = \pm \dfrac{{A\omega }}{{\sqrt {3 + 1} }} = \pm 20\pi cm/s\)
Câu 15 :
Một vật dao động điều hòa với tần số góc $ω$, khi thế năng bằng $3$ lần động năng thì li độ $x$ và vận tốc $v$ của vật có mối liên hệ với nhau như thế nào?
Đáp án : D Phương pháp giải :
Áp dụng biểu thức xác định li độ, vận tốc dao động của vật khi biết Wt = nWđ : \(\left\{ \begin{array}{l}{W_t} = n{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{n}{{n + 1}}W\\{W_d} = \dfrac{1}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm A\sqrt {\dfrac{n}{{n + 1}}} \\v = \pm \dfrac{{A\omega }}{{\sqrt {n + 1} }}\end{array} \right.\) Lời giải chi tiết :
Khi Wt = 3Wđ \(\left\{ \begin{array}{l}{W_t} = 3{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{3}{{3 + 1}}W\\{W_d} = \dfrac{1}{{3 + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm A\sqrt {\dfrac{3}{{3 + 1}}} \\v = \pm \dfrac{{A\omega }}{{\sqrt {3 + 1} }}\end{array} \right. \to \dfrac{x}{v} = \dfrac{{\sqrt 3 }}{\omega }\)
Câu 16 :
Một lò xo có độ cứng k treo thẳng đứng vào điểm cố định, đầu dưới có vật $m = 100 (g)$. Vật dao động điều hòa với tần số $f = 5 Hz$, cơ năng là $W=0,08J$ . Lấy $g = 10 m/s^2$, \({\pi ^2} = 10\). Tỉ số động năng và thế năng tại li độ $x = 2 cm$ là:
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức xác định thế năng của con lắc lò xo: \({{\rm{W}}_t} = \dfrac{1}{2}k{{\rm{x}}^2}\) + Áp dụng biểu thức cơ năng: \({\text{W}} = {{\text{W}}_t} + {{\text{W}}_d}\) Lời giải chi tiết :
Tần số góc: \(\omega = 2\pi f = 10\pi (ra{\rm{d}}/s)\) Tại li độ $x = 2cm$ có: + Thế năng: \({{\rm{W}}_t} = \dfrac{1}{2}k{{\rm{x}}^2} = \dfrac{1}{2}m{\omega ^2}{x^2} = \dfrac{1}{2}0,1.{(10\pi )^2}{(0,02)^2} = 0,02J\) + Động năng: \({{\text{W}}_d} = {\text{W - }}{{\text{W}}_t} = 0,08 - 0,02 = 0,06J\) \(\dfrac{{{{\text{W}}_d}}}{{{{\text{W}}_t}}} = \dfrac{{0,06}}{{0,02}} = 3\)
Câu 17 :
Ở một thời điểm, vận tốc của một vật dao động điều hòa bằng 20% vận tốc cực đại, tỉ số giữa động năng và thế năng của vật là:
Đáp án : B Phương pháp giải :
+ Áp dụng hệ thức độc lập A-x-v: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) + Áp dụng biểu thức xác định động năng của vật: \({{\text{W}}_d} = \dfrac{1}{2}m{v^2}\) + Áp dụng biểu thức xác định thế năng của vật: \({{\rm{W}}_t} = \dfrac{1}{2}k{{\rm{x}}^2}\) Lời giải chi tiết :
Khi v = 20%vmax = 0,2 Aω Áp dụng hệ thức độ lập ta có: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \to {x^2} = {A^2} - \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} - \dfrac{{{{(0,2A\omega )}^2}}}{{{\omega ^2}}} = 0,96{A^2}\) Khi đó, ta có: + Động năng của vật: \({{\text{W}}_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{(0,2)^2}{\omega ^2}{A^2}\) + Thế năng của vật: \({{\rm{W}}_t} = \dfrac{1}{2}k{{\rm{x}}^2} = \dfrac{1}{2}m{\omega ^2}{x^2} = \dfrac{1}{2}m{\omega ^2}0,96.{A^2}\) \(\dfrac{{{{\text{W}}_d}}}{{{{\text{W}}_t}}} = \dfrac{{\dfrac{1}{2}m{{(0,2)}^2}{\omega ^2}{A^2}}}{{\dfrac{1}{2}m{\omega ^2}0,96.{A^2}}} = \dfrac{1}{{24}}\)
Câu 18 :
Một vật dao động điều hòa với chu kỳ T và biên độ là A. Khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là?
Đáp án : B Phương pháp giải :
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Ta có: \({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x = \pm \dfrac{A}{{\sqrt 2 }}\) 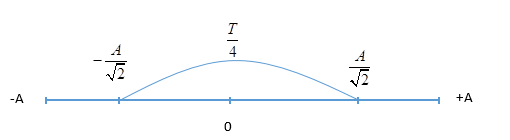 Ta có, khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là \(\dfrac{T}{4}\)
Câu 19 :
Một vật dao động điều hòa với chu kỳ T và biên độ là A. Ban đầu vật ở vị trí cân bằng, khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà động năng bằng thế năng là:
Đáp án : B Phương pháp giải :
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Vị trí: \({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x = \pm \dfrac{A}{{\sqrt 2 }}\)  => Khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà động năng bằng thế năng là: \(\dfrac{T}{8}\)
Câu 20 :
Con lắc lò xo dao động theo phương ngang với phương trình \(x = Acos(\omega t + \varphi )\). Cứ sau những khoảng thời gian bằng nhau và bằng \(\dfrac{\pi }{{40}}\left( s \right)\) thì động năng của vật bằng thế năng của lò xo. Con lắc dao động điều hoà với tần số góc:
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\) + Sử dụng trục thời gian suy ra từ vòng tròn + Áp dụng biểu thức mối liên hệ giữa tần số góc và chu kì dao động: \(\omega = \frac{{2\pi }}{T}\) Lời giải chi tiết :
Ta có: \({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x = \pm \frac{A}{{\sqrt 2 }}\) 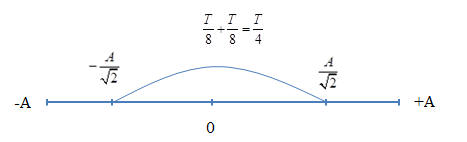 Ta có, khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là \(\dfrac{T}{4}\) Theo đầu bài, ta có: \(\begin{array}{l}\dfrac{\pi }{{40}} = \dfrac{T}{4} \to T = \dfrac{\pi }{{10}}\\\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{\dfrac{\pi }{{10}}}} = 20(ra{\rm{d}}/s)\end{array}\)
Câu 21 :
Một chất điểm có khối lượng m = 1 kg dao động điều hoà với chu kì T = π/5 (s). Biết năng lượng của nó là 0,02 J. Biên độ dao động của chất điểm là:
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính tần số góc: \(\omega = \dfrac{{2\pi }}{T}\) + Áp dụng biểu thức tính cơ năng: \({\rm{W = }}\dfrac{1}{2}m{\omega ^2}{A^2}\) Lời giải chi tiết :
Ta có: tần số góc \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{\dfrac{\pi }{5}}} = 10(ra{\rm{d}}/s)\) Cơ năng của dao động: \({\rm{W = }}\dfrac{1}{2}m{\omega ^2}{A^2} \to A = \sqrt {\dfrac{{2{\rm{W}}}}{{m{\omega ^2}}}} = \sqrt {\dfrac{{2.0,02}}{{1{{(10)}^2}}}} = 0,02m = 2cm\)
Câu 22 :
Một chất điểm dao động điều hòa theo phương trình x = Acos(4πt – π/6) cm. Trong một giây đầu tiên từ thời điểm t = 0, chất điểm qua li độ mà động năng bằng thế năng bao nhiêu lần?
Đáp án : D Phương pháp giải :
+ Áp dụng biểu thức xác định chu kì dao động: \(T = \dfrac{{2\pi }}{\omega }\) + Xác định vị trí tại thời điểm ban đầu: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi \\v = - A\omega \sin \varphi \end{array} \right.\) + Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\) Lời giải chi tiết :
Chu kì dao động của chất điểm: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\) Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\left( { - \dfrac{\pi }{6}} \right) = \dfrac{{A\sqrt 3 }}{2}\\v = - A\omega \sin \left( { - \dfrac{\pi }{6}} \right) > 0\end{array} \right.\) Tại vị trí: \({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x = \pm \dfrac{A}{{\sqrt 2 }}\) Ta có: $1s = 2T$ => Sau $1s$, chất điểm lại quay về vị trí ban đầu Mặt khác, trong $1$ chu kì chất điểm đi qua li độ mà động năng bằng thế năng $4$ lần => Trong $1s (2T)$ chất điểm đi qua li độ có động năng bằng thế năng $2.4 = 8$ lần
Câu 23 :
Một con lắc lò xo có m = 100 (g) dao động điều hoà với cơ năng W = 2 mJ và gia tốc cực đại amax = 80 cm/s2. Biên độ và tần số góc của dao động là:
Đáp án : B Phương pháp giải :
+ Áp dụng biểu thức tính cơ năng:\({\rm{W = }}\dfrac{1}{2}m{\omega ^2}{A^2}\) + Áp dụng biểu thức tính gia tốc cực đại: \({a_{{\rm{max}}}} = {\omega ^2}A\) Lời giải chi tiết :
Ta có: + Cơ năng: \({\rm{W = }}\dfrac{1}{2}m{\omega ^2}{A^2}\) + Gia tốc cực đại: \({a_{{\rm{max}}}} = {\omega ^2}A\) \( \to \dfrac{{\rm{W}}}{{{a_{{\rm{max}}}}}} = \dfrac{{mA}}{2} = \dfrac{{{{2.10}^{ - 3}}}}{{0,8}} = 2,{5.10^{ - 3}} \to A = \dfrac{{2.2,{{5.10}^{ - 3}}}}{m} = \dfrac{{2.2,{{5.10}^{ - 3}}}}{{0,1}} = 0,05m = 5cm\) thay vào amax \( \to \omega = \sqrt {\dfrac{{{a_{{\rm{max}}}}}}{A}} = \sqrt {\dfrac{{0,8}}{{0,05}}} = 4{\rm{r}}a{\rm{d}}/s\)
Câu 24 :
Một con lắc lò xo dao động điều hòa gồm vật nặng có khối lượng \(m = 100g\) , đồ thị thế năng theo thời gian của con lăc như hình vẽ. Biết \({t_2} - {t_1} = 0,05s\), lấy \({\pi ^2} = 10\) . Biên độ và chu kì dao động của con lắc là: 
Đáp án : C Phương pháp giải :
+ Đọc đồ thị \({W_t} - {\rm{ }}t\) + Thế năng dao động tuần hoàn với chu kì: \(T' = \dfrac{T}{2}\) + Áp dụng biểu thức tính thế năng cực đại: \({{\rm{W}}_{{t_{{\rm{max}}}}}}{\rm{ = }}\dfrac{1}{2}m{\omega ^2}{A^2}\) Lời giải chi tiết :
Gọi \(T'\): chu kì tuần hoàn của thế năng Ta có: \(T' = \dfrac{T}{2}\) Từ đồ thị Wt - t, ta có: \(\begin{array}{l}{t_2} - {t_1} = {\rm{ }}0,05s = T' = \dfrac{T}{2} \to T = 0,1s\\ \to \omega = \dfrac{{2\pi }}{T} = 20\pi \left( {rad/s} \right)\end{array}\) \({{\rm{W}}_{{t_{{\rm{max}}}}}}{\rm{ = }}\dfrac{1}{2}m{\omega ^2}{A^2} = 3,{2.10^{ - 3}} \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{t_{{\rm{max}}}}}}}}{{m{\omega ^2}}}} = \sqrt {\dfrac{{2.3,{{2.10}^{ - 3}}}}{{0,1{{(20\pi )}^2}}}} = {4.10^{ - 3}}m = 0,4cm\)
Câu 25 :
Một vật có khối lượng $400g$ dao động điều hòa có đồ thị động năng như hình vẽ. Tại thời điểm $t = 0$ vật đang chuyển động theo chiều dương, lấy $\pi^2=10$. Phương trình dao động của vật là: 
Đáp án : D Phương pháp giải :
+ Đọc đồ thị Wđ - t + Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\) + Áp dụng biểu thức tính động năng cực đại: \({{\rm{W}}_{{{\rm{d}}_{{\rm{max}}}}}} = \dfrac{1}{2}m{\omega ^2}{A^2}\) + Viết phương trình dao động điều hòa Lời giải chi tiết :
Từ đồ thị, ta có: + Tại thời điểm ban đầu (t =0) : \(\begin{array}{l}{{\rm{W}}_d} = 0,015 \to {{\rm{W}}_t} = 0,02 - 0,015 = {5.10^{ - 3}}J = \dfrac{{\rm{W}}}{4}\\ \to {x_0} = \pm \dfrac{A}{2}\end{array}\) + Vị trí có Wđ = 0 lần thứ nhất: <=> x1 = ±A Dựa vào đồ thị ta suy ra: x0 = A/2 và x1 = A => Khoảng thời gian vật đi từ x0 đến x1 là: \(\Delta t = \dfrac{T}{6} = \dfrac{1}{6}s \to T = 1{\rm{s}} \to \omega = \dfrac{{2\pi }}{T} = 2\pi (ra{\rm{d}}/s)\) \({{\rm{W}}_{{{\rm{d}}_{{\rm{max}}}}}} = \dfrac{1}{2}m{\omega ^2}{A^2} = 0,02 \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{d_{{\rm{max}}}}}}}}{{m{\omega ^2}}}} = \sqrt {\dfrac{{2.0,02}}{{0,4.{{(2\pi )}^2}}}} = 0,05m = 5cm\) Tại t = 0: \(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\varphi {\rm{ = }}\dfrac{A}{2}\\v = - {\rm{Asin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{3}\) => Phương trình dao động của vật: \(x = 5c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{3}} \right)cm\)
Câu 26 :
Con lắc lò xo dao động điều hòa trên mặt phẳng ngang không ma sát. Khi vật ở vị trí biên, ta giữ chặt một phần của lò xo làm cơ năng của vật giảm \(10\% \) thì biên độ dao động của hệ vật sẽ
Đáp án : C Phương pháp giải :
Cơ năng của con lắc lò xo: \({\rm{W}} = \dfrac{1}{2}k{A^2}\) Cắt lò xo: \(k'\Delta l' = k\Delta l\) Lời giải chi tiết :
Cơ năng ban đầu của con lắc là: \({\rm{W}} = \dfrac{1}{2}k{A^2}\) Giữ chặt một phần của lò xo, biên độ mới của con lắc và độ cứng của lò xo: \(k'A' = kA \Rightarrow k' = \dfrac{{kA}}{{A'}}\) Cơ năng của con lắc giảm 10%, cơ năng còn lại là: \(\begin{array}{l}{\rm{W}}' = \dfrac{1}{2}k'A{'^2} = 0,9W = 0,9.\dfrac{1}{2}k{A^2}\\ \Rightarrow \dfrac{{kA}}{{A'}}.A{'^2} = 0,9.k{A^2} \Rightarrow A' = 0,9A = A.90\% \\ \Rightarrow A - A' = A.10\% \end{array}\)
Câu 27 :
Một vật nặng gắn vào một lò xo nhẹ có độ cứng k = 20 N/m thực hiện dao động điều hoà với biên độ A = 5cm. Động năng của vật khi nó cách vị trí cân bằng 4 cm là
Đáp án : C Phương pháp giải :
Thế năng của con lắc lò xo: \({{\text{W}}_{t}}=\frac{1}{2}k{{x}^{2}}\) Cơ năng của con lắc: \(\text{W}={{\text{W}}_{t}}+{{\text{W}}_{d}}=\frac{1}{2}k{{A}^{2}}\) Lời giải chi tiết :
Áp dụng định lí bảo toàn cơ năng cho con lắc, ta có: \(\begin{align}& \text{W}={{\text{W}}_{t}}+{{\text{W}}_{d}}\Rightarrow \frac{1}{2}k{{A}^{2}}=\frac{1}{2}k{{x}^{2}}+{{\text{W}}_{d}} \\& \Rightarrow {{\text{W}}_{d}}=\frac{1}{2}k{{A}^{2}}-\frac{1}{2}k{{x}^{2}}=0,009\,\,\left( J \right) \\\end{align}\)
Câu 28 :
Một con lắc lò xo có độ cứng \(k\), khối lượng vật nhỏ \(m\) dao động điều hoà. Tại thời điểm mà li độ và vận tốc của vật tương ứng là \(x\) và \(v\) thì động năng của vật là
Đáp án : C Phương pháp giải :
Công thức tính động năng: \({{\rm{W}}_d} = \frac{1}{2}m{v^2}.\) Lời giải chi tiết :
Động năng của vật là:\({{\rm{W}}_d} = \frac{1}{2}m{v^2}.\)
Câu 29 :
Xét một con lắc lò xo gồm vật nhỏ và lò xo nhẹ dao động điều hòa trên mặt phẳng nằm ngang với biên độ A. Chọn gốc thế năng tại vị trí cân bằng. Tại vị trí con lắc có động năng bằng cơ năng, li độ của vật có giá trị là:
Đáp án : B Phương pháp giải :
Sử dụng công thức năng lượng của con lắc lò xo. Lời giải chi tiết :
Ta có: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\) \( \Leftrightarrow \dfrac{1}{2}k{A^2} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{{\rm{x}}^2}\) Tại VTCB thế năng bằng 0. Vị trí con lắc có động năng bằng cơ năng => là vị trí động năng cực đại => VTCB. Tại VTCB, li độ x = 0.
Câu 30 :
Động năng dao động của một con lắc lò xo được mô tả theo thế năng dao động của nó bằng đồ thị như hình vẽ. Cho biết khối lượng của vật bằng \(100\,\,g\), vật dao động giữa hai vị trí cách nhau \(8\,\,cm\). Tần số góc của dao động
Đáp án : C Phương pháp giải :
Sử dụng kĩ năng đọc đồ thị Độ dài quỹ đạo dao động: \(L = 2A\) Thế năng của con lắc lò xo: \({{\rm{W}}_t} = \dfrac{1}{2}m{\omega ^2}{x^2}\) Lời giải chi tiết :
Độ dài quỹ đạo dao động của con lắc là: \(L = 2A \Rightarrow A = \dfrac{L}{2} = \dfrac{8}{2} = 4\,\,\left( {cm} \right) = 0,04\,\,\left( m \right)\) Từ đồ thị ta thấy khi động năng bằng 0, thế năng của con lắc: \(\begin{array}{l}{{\rm{W}}_{t\max }} = \dfrac{1}{2}m{\omega ^2}{A^2} = {4.10^{ - 3}}\,\,\left( J \right)\\ \Rightarrow \dfrac{1}{2}0,1.{\omega ^2}.0,{04^2} = {4.10^{ - 3}} \Rightarrow \omega = 5\sqrt 2 \,\,\left( {rad/s} \right)\end{array}\)
|



















Danh sách bình luận