Trắc nghiệm Bài 1. Bài tập quãng đường, tốc độ trung bình - Vật Lí 12Đề bài
Câu 1 :
Một vật dao động điều hòa theo phương trình $x = A\cos (\omega t + \varphi )cm$. Quãng đường vật đi được sau $n$ chu kì là?
Câu 2 :
Một vật nhỏ dao động điều hòa với biên độ $4cm$ và chu kì $2s$. Quãng đường vật đi được trong $4s$ là:
Câu 3 :
Một vật dao động điều hòa, trong $1$ phút thực hiện được $30$ dao động toàn phần. Quãng đường mà vật di chuyển trong $8s$ là $64cm$. Biên độ dao động của vật là:
Câu 4 :
Khi nói về một vật dao động điều hòa có biên độ $A$ và chu kì $T$, với mốc thời gian $(t = 0)$ là lúc vật ở vị trí biên, phát biểu nào sau đây là sai?
Câu 5 :
Vật dao động điều hoà theo phương trình $x = 10\cos \left( {\pi t - \dfrac{\pi }{2}} \right)cm$. Quãng đường vật đi được trong khoảmg thời gian từ ${t_1} = 1,5s$ đến ${t_2} = \dfrac{{13}}{3}s$ là:
Câu 6 :
Một vật dao động điều hòa theo phương trình \(x = 4c{\rm{os}}\left( {10\pi t - \dfrac{\pi }{4}} \right)cm\) (t tính bằng giây). Tìm quãng đường vật đi được kể từ lúc bắt đầu dao động đến khi vật có tốc độ \(0,2\pi \sqrt 3 m/s\) lần thứ hai?
Câu 7 :
Một vật dao động điều hòa với biên độ $10 cm$, tần số $2Hz$. Tại thời điểm $t = 0$ vật chuyển động theo chiều dương và đến thời điểm $t = 2s$ vật có gia tốc \(80{\pi ^2}\sqrt 2 \) (cm/s2). Tính quãng đường vật đi được từ lúc $t = 0$ đến khi $t = 2,625s$
Câu 8 :
Một chất điểm dao động điều hoà thẳng trên trục $x'x$ xung quanh vị trí cân bằng $x = 0$ với chu kì dao động $T = 1,57s\left( { \approx \dfrac{\pi }{2}s} \right)$. Tại thời điểm $t = 0$ nó qua toạ độ ${x_0} = 25cm$ với vận tốc ${v_0} = 100cm/s$. Quãng đường vật đi được sau thời điểm $t = 0$ một thời gian $\dfrac{\pi }{8}s$ là :
Câu 9 :
Một vật dao động điều hoà với phương trình $x = A\cos \left( {\omega t + \dfrac{\pi }{3}} \right)cm$. Biết quãng đường vật đi được trong thời gian $1s$ tính từ thời điểm gốc là $2A$ và trong $\dfrac{2}{3}s$ là $9cm$. Giá trị của $A$ và $ω$ là:
Câu 10 :
Một vật dao động điều hòa theo phương trình $x = 5\cos \left( {\dfrac{{2\pi }}{3}t - \frac{\pi }{3}} \right)cm$. Kể từ thời điểm $t = 0$, sau thời gian bao lâu thì vật đi được quãng đường $7,5 cm$.
Câu 11 :
Một vật dao động điều hoà dọc theo trục $Ox$, quanh vị trí cân bằng $O$ với biên độ $A$ và chu kỳ $T$. Trong khoảng thời gian $T/4$, quãng đường lớn nhất mà vật có thể đi được là:
Câu 12 :
Một vật dao động điều hòa với biên độ $4 cm$. Trong $3,2s$ quãng đường dài nhất mà vật đi được là $18 cm$. Hỏi trong $2,3s$ thì quãng đường ngắn nhất mà vật đi được là bao nhiêu?
Câu 13 :
Một vật dao động điều hòa với biên độ $10 cm$, tần số góc $2\pi \left( {rad/s} \right)$. Thời gian ngắn nhất để vật đi được quãng đường $16,2 cm$.
Câu 14 :
Một vật dao động điều hòa với biên độ $10 cm$, tần số góc \(2\pi ra{\rm{d}}/s\). Thời gian dài nhất để vật đi được quãng đường $16,2 cm.$
Câu 15 :
Một vật dao động điều hòa với biên độ $A$, chu kì $T$. Tốc độ trung bình của vật trong một chu kì là:
Câu 16 :
Một vật dao động điều hòa có độ lớn vận tốc cực đại là $31,4 cm/s$. Lấy $\pi = 3,14$. Tốc độ trung bình của vật trong một chu kì dao động là:
Câu 17 :
Vật dao động điều hoà theo phương trình $x = 5\cos \left( {2\pi t - \frac{\pi }{4}} \right)cm$. Tốc độ trung bình của vật đi được trong khoảng thời gian từ ${t_1} = 1s$ đến ${t_2} = 4,625s$ là:
Câu 18 :
Một vật dao động điều hòa có phương trình $x = 5c{\rm{os}}\left( {4\pi t + \frac{\pi }{3}} \right)\left( {cm,s} \right)$. Tốc độ trung bình của vật trong khoảng thời gian tính từ lúc bắt đầu khảo sát dao động đến thời điểm vật đi qua vị trí cân bằng theo chiều dương lần thứ nhất là:
Câu 19 :
Một chất điểm đang dao động với phương trình: $x = 6\cos \left( {10\pi t} \right)cm$. Tính tốc độ trung bình của chất điểm sau $1/4$ chu kì tính từ khi bắt đầu dao động và tốc độ trung bình sau nhiều chu kỳ dao động:
Câu 20 :
Một vật nhỏ dao động điều hòa trên đoạn thẳng dài L, chu kỳ T. Quãng đường lớn nhất vật đi được trong khoảng thời gian\(\dfrac{{5T}}{3}\) là
Câu 21 :
Một vật dao động điều hòa với biên độ $A$ và chu kỳ $T$. Tìm tốc độ trung bình nhỏ nhất của vật trong $T/3$?
Câu 22 :
Vật đang dao động điều hòa dọc theo đường thẳng. Một điểm $M$ nằm trên đường thẳng đó, phía ngoài khoảng chuyển động của vật, tại thời điểm t thì vật xa điểm $M$ nhất, sau đó một khoảng thời gian ngắn nhất là $\Delta t$ thì vật gần điểm $M$ nhất. Độ lớn vận tốc của vật sẽ đạt được cực đại vào thời điểm:
Câu 23 :
Một chất điểm dao động điều hòa với chu kì $T$. Trong khoảng thời gian ngắn nhất khi đi từ vị trí biên có li độ $x = A$ đến vị trí $x = - \dfrac{A}{2}$, chất điểm có tốc độ trung bình là:
Câu 24 :
Một vật dao động điều hòa trên trục Ox theo phương trình \(x = A\cos \left( {\dfrac{\pi }{3}t + \varphi } \right)\) ( t tính bằng giây). Trong ba khoảng thời gian theo thứ tự liên tiếp là \(\Delta t = 1s;\Delta {t_2} = \Delta {t_3} = 2s\) thì quãng đường chuyển động của vật lần lượt là \({S_1} = 5cm;{S_2} = 15cm\) và quãng đường S3. Quãng đường S3 gần nhất với giá trị nào sau đây:
Lời giải và đáp án
Câu 1 :
Một vật dao động điều hòa theo phương trình $x = A\cos (\omega t + \varphi )cm$. Quãng đường vật đi được sau $n$ chu kì là?
Đáp án : B Lời giải chi tiết :
Trong $n$ chu kì, vật đi được quãng đường: $S=n.4A$
Câu 2 :
Một vật nhỏ dao động điều hòa với biên độ $4cm$ và chu kì $2s$. Quãng đường vật đi được trong $4s$ là:
Đáp án : A Phương pháp giải :
Sử dụng công thức xác định quãng đường vật đi được trong $n$ chu kì là $S = n.4A$ Lời giải chi tiết :
Ta có: $T = 2s => 4s = 2T$ Quãng đường vật đi được trong $4s = 2T$ là $S = 2.4A = 2.4.4= 32cm$
Câu 3 :
Một vật dao động điều hòa, trong $1$ phút thực hiện được $30$ dao động toàn phần. Quãng đường mà vật di chuyển trong $8s$ là $64cm$. Biên độ dao động của vật là:
Đáp án : C Phương pháp giải :
+ Sử dụng công thức tính chu kì dao động: \(T = \dfrac{{\Delta t}}{N}\) + Sử dụng công thức xác định quãng đường vật đi được trong n chu kì là $S = n.4A$ Lời giải chi tiết :
Ta có: Chu kì dao động: \(T = \dfrac{{\Delta t}}{N} = \dfrac{{60}}{{30}} = 2{\rm{s}}\) Quãng đường vật đi được trong $8s = 4T$ là $S = 4.4A = 64cm => A = 4cm$
Câu 4 :
Khi nói về một vật dao động điều hòa có biên độ $A$ và chu kì $T$, với mốc thời gian $(t = 0)$ là lúc vật ở vị trí biên, phát biểu nào sau đây là sai?
Đáp án : A Phương pháp giải :
+ Sử dụng trục thời gian suy ra từ đường tròn + Sử phương pháp đại số xác định quãng đường đi được của vật 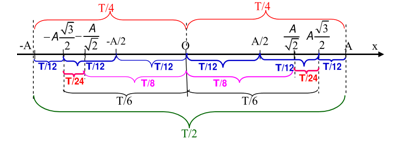 Lời giải chi tiết :
Ta có: t = 0, x0 = A A - sai vì sau T/8 vật ở vị trí có li độ \(x = \frac{{A\sqrt 2 }}{2} \to S = A - \frac{{A\sqrt 2 }}{2}\) B, C, D - đúng
Câu 5 :
Vật dao động điều hoà theo phương trình $x = 10\cos \left( {\pi t - \dfrac{\pi }{2}} \right)cm$. Quãng đường vật đi được trong khoảmg thời gian từ ${t_1} = 1,5s$ đến ${t_2} = \dfrac{{13}}{3}s$ là:
Đáp án : A Phương pháp giải :
+ Xác định vị trí tại thời điểm t (x,v) + Xác định khoảng thời gian ∆t + Sử dụng phương pháp đại số xác định quãng đường vật đi được từ li độ x1 đến x2 Lời giải chi tiết :
Tại t1 = 1,5s: \(\left\{ \begin{array}{l}{x_1} = 10c{\rm{os}}\left( {\pi .1,5 - \frac{\pi }{2}} \right) = - 10\\{v_1} = - A\omega \sin \left( {\pi .1,5 - \frac{\pi }{2}} \right) = 0\end{array} \right.\) Tại t2 = 13/3s: \(\left\{ \begin{array}{l}{x_2} = 10c{\rm{os}}\left( {\pi .\frac{{13}}{3} - \frac{\pi }{2}} \right) = 5\sqrt 3 \\{v_2} = - A\omega \sin \left( {\pi .\frac{{13}}{3} - \frac{\pi }{2}} \right) > 0\end{array} \right.\) \(\Delta t = {t_2} - {t_1} = \frac{{13}}{3} - 1,5 = \frac{{17}}{6}s = T + \frac{{5T}}{{12}}\) => Quãng đường vật đi được từ t1 đến t2 là: \(S = 4A + A + \frac{{A\sqrt 3 }}{2} = 5.10 + 5\sqrt 3 = 50 + 5\sqrt 3 \left( {cm} \right)\) 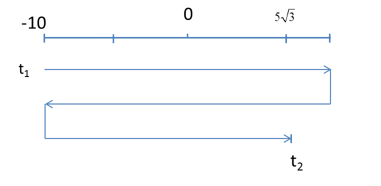
Câu 6 :
Một vật dao động điều hòa theo phương trình \(x = 4c{\rm{os}}\left( {10\pi t - \dfrac{\pi }{4}} \right)cm\) (t tính bằng giây). Tìm quãng đường vật đi được kể từ lúc bắt đầu dao động đến khi vật có tốc độ \(0,2\pi \sqrt 3 m/s\) lần thứ hai?
Đáp án : C Phương pháp giải :
+ Sử dụng phương pháp đại số xác định quãng đường vật đi được từ li độ x1 đến x2 + Sử dụng hệ thức độc lập: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\) Lời giải chi tiết :
Tại $t=0$: \(\left\{ \begin{array}{l}{x_0} = 4c{\rm{os}}\left( {\frac{-\pi }{4}} \right) = 2\sqrt 2 cm\\v = - 40\pi \sin \left( {\frac{-\pi }{4}} \right) = 20\pi \sqrt 2 > 0\end{array} \right.\) Tại $v=$\(0,2\pi \sqrt 3 m/s\): \(x = \pm \sqrt {{A^2} - \frac{{{v^2}}}{{{\omega ^2}}}} = \pm \sqrt {0,{{04}^2} - \frac{{{{\left( {0,2\pi \sqrt 3 } \right)}^2}}}{{{{\left( {10\pi } \right)}^2}}}} = \pm 0,02m = \pm 2cm\) => Quãng đường vật đi được: \(S = {\rm{ }}(4 - 2\sqrt 2 ) + 4 + 2 = 10 - 2\sqrt 2 cm\)
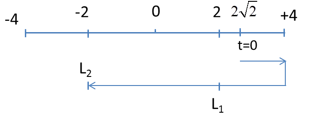
Câu 7 :
Một vật dao động điều hòa với biên độ $10 cm$, tần số $2Hz$. Tại thời điểm $t = 0$ vật chuyển động theo chiều dương và đến thời điểm $t = 2s$ vật có gia tốc \(80{\pi ^2}\sqrt 2 \) (cm/s2). Tính quãng đường vật đi được từ lúc $t = 0$ đến khi $t = 2,625s$
Đáp án : C Phương pháp giải :
+ Áp dụng các công thức xác định chu kì và tần số góc: \(T = \frac{1}{f}\)và \(\omega = 2\pi f\) + Xác định vị trí tại thời điểm ban đầu (x, v) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Ta có, chu kì dao động của vật: \(T = \frac{1}{f} = \frac{1}{2} = 0,5s\), tần số góc: \(\omega = 2\pi f = 4\pi (ra{\rm{d}}/s)\) Biên độ A = 10cm. Tại t = 2s: $a = 80{\pi ^2}\sqrt 2 = - {\omega ^2}x \to x = - \frac{{80{\pi ^2}\sqrt 2 }}{{{{\left( {4\pi } \right)}^2}}} = - 5\sqrt 2 cm{\rm{ }}$ Mặt khác ta có khoảng thời gian vật chuyển động từ t = 0 đến t = 2s là: \(\Delta t = 2s = 4T\) => tại t = 2s vật quay lại vị trí ban đầu. => Tại t = 0: \(\left\{ \begin{array}{l}{x_0} = - 5\sqrt 2 cm\\v > 0\end{array} \right.\) Khoảng thời gian vật chuyển động từ t = 0 đến t = 2,625s là \(\Delta t = 2,625s = 5T + \frac{T}{4}\) => Quãng đường mà vật đi được từ t = 0 đến t = 2,625s là: \(S = 5.4{\rm{A}} + A\sqrt 2 = 200 + 10\sqrt 2 = 214,14cm\) 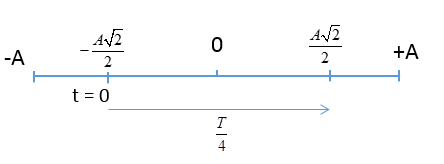
Câu 8 :
Một chất điểm dao động điều hoà thẳng trên trục $x'x$ xung quanh vị trí cân bằng $x = 0$ với chu kì dao động $T = 1,57s\left( { \approx \dfrac{\pi }{2}s} \right)$. Tại thời điểm $t = 0$ nó qua toạ độ ${x_0} = 25cm$ với vận tốc ${v_0} = 100cm/s$. Quãng đường vật đi được sau thời điểm $t = 0$ một thời gian $\dfrac{\pi }{8}s$ là :
Đáp án : C Phương pháp giải :
+ Áp dụng biểu thức xác định tần số góc của dao động: \(\omega = \frac{{2\pi }}{T}\) + Áp dụng hệ thức độc lập A - x - v: \({A^2} = {x^2} + {\left( {\frac{v}{\omega }} \right)^2}\) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Ta có: Tần số góc của dao động: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{\frac{\pi }{2}}} = 4({\rm{r}}a{\rm{d}}/s)\) - Tại t = 0: x0 = 25cm, v = 100 cm/s Sử dụng hệ thức độc lập, ta có: \({A^2} = {x^2} + {\left( {\frac{v}{\omega }} \right)^2} = {25^2} + {\left( {\frac{{100}}{4}} \right)^2} \to A = 25\sqrt 2 cm\) Khoảng thời gian từ t = 0 đến một khoảng \(\Delta t = \frac{\pi }{8}s = \frac{T}{4}\) Quãng đường vật đi được sau thời điểm t = 0 một thời gian p/8 s là: \(S = 2(A - \frac{A}{{\sqrt 2 }}) = 50\sqrt 2 - 50 = 20,711cm\) 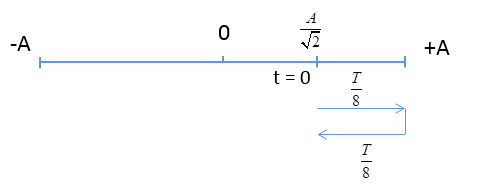
Câu 9 :
Một vật dao động điều hoà với phương trình $x = A\cos \left( {\omega t + \dfrac{\pi }{3}} \right)cm$. Biết quãng đường vật đi được trong thời gian $1s$ tính từ thời điểm gốc là $2A$ và trong $\dfrac{2}{3}s$ là $9cm$. Giá trị của $A$ và $ω$ là:
Đáp án : B Phương pháp giải :
+ Quãng đường vật đi được $2A$ trong khoảng thời gian $\dfrac{T}{2}$ + Áp dụng công tính tần số góc: \(\omega = \dfrac{{2\pi }}{T}\) + Xác định vị trí của vật tại thời điểm ban đầu \(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\varphi \\v = - A\sin \varphi \end{array} \right.\) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Ta có khoảng thời gian vật đi được quãng đường $2A$ là $\dfrac{T}{2}$ \( \to \dfrac{T}{2} = 1{\rm{s}} \to T = 2{\rm{s}} \to \omega {\rm{ = }}\dfrac{{2\pi }}{T} = \pi ({\rm{r}}a{\rm{d/s)}}\) Tại $t = 0$: \(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\dfrac{\pi }{3} = \dfrac{A}{2}\\v = - A\omega\sin \dfrac{\pi }{3} < 0\end{array} \right.\) 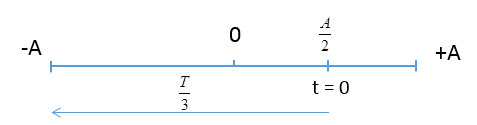 Trong khoảng thời gian \(\Delta t = \dfrac{2}{3}s = \dfrac{T}{3}\) từ thời điểm gốc vật đi được quãng đường $S = 9cm$ Ta có: \(S = \dfrac{A}{2} + A = 1,5A = 9cm \to A = 6cm\)
Câu 10 :
Một vật dao động điều hòa theo phương trình $x = 5\cos \left( {\dfrac{{2\pi }}{3}t - \frac{\pi }{3}} \right)cm$. Kể từ thời điểm $t = 0$, sau thời gian bao lâu thì vật đi được quãng đường $7,5 cm$.
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức xác định chu kì dao động \(T = \dfrac{{2\pi }}{\omega }\) + Xác định vị trí của vật tại thời điểm ban đầu \(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\varphi \\v = - A\sin \varphi \end{array} \right.\) + Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Chu kì dao động của vật: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{{2\pi }}{3}}} = 3s\) Tại t = 0: \(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os( - }}\frac{\pi }{3}) = \frac{A}{2}\\v = - A\sin ( - \frac{\pi }{3}) > 0\end{array} \right.\) S = 7,5 cm = 1,5A => Kể từ t = 0, vật đi được quãng đường 1,5A trong khoảng thời gian: \(\Delta t = \frac{T}{6} + \frac{T}{4} = \frac{{5T}}{{12}} = \frac{{5.3}}{{12}} = 1,25{\rm{s}}\) 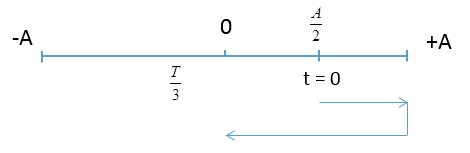
Câu 11 :
Một vật dao động điều hoà dọc theo trục $Ox$, quanh vị trí cân bằng $O$ với biên độ $A$ và chu kỳ $T$. Trong khoảng thời gian $T/4$, quãng đường lớn nhất mà vật có thể đi được là:
Đáp án : D Phương pháp giải :
Áp dụng công thức tính quãng đường lớn nhất: \({S_{{\rm{max}}}} = 2{\rm{Asin}}\frac{{\omega \Delta t}}{2}\) Lời giải chi tiết :
Quãng đường lớn nhất vật đi được trong khoảng thời gian \(\frac{T}{4}\) là: \({S_{{\rm{max}}}} = 2{\rm{Asin}}\frac{{\omega \Delta t}}{2} = 2{\rm{Asin}}\frac{{\omega \frac{T}{4}}}{2} = 2{\rm{Asin}}\frac{{\frac{{2\pi }}{T}\frac{T}{4}}}{2} = 2{\rm{Asin}}\frac{\pi }{4} = A\sqrt 2 \)
Câu 12 :
Một vật dao động điều hòa với biên độ $4 cm$. Trong $3,2s$ quãng đường dài nhất mà vật đi được là $18 cm$. Hỏi trong $2,3s$ thì quãng đường ngắn nhất mà vật đi được là bao nhiêu?
Đáp án : C Phương pháp giải :
+ Áp dụng công thức tính quãng đường lớn nhất: \({S_{{\rm{max}}}} = 2{\rm{Asin}}\dfrac{{\omega \Delta t}}{2}\) + Áp dụng công thức tính quãng đường ngắn nhất: \({S_{Min}} = 2A(1 - c{\rm{os}}\dfrac{{\Delta \varphi }}{2})\) Lời giải chi tiết :
Trong \(3,2s\) \(S_{max}= 18cm = 4.4 + 2 = 4A+ 2\) => t1 = T + ∆t1 Quãng đường lớn nhất vật đi được trong khoảng thời gian \(3,2s\) là: \(\begin{array}{l}{S_{{\rm{max}}}} = 4A + 2{\rm{Asin}}\dfrac{{\omega \Delta {t_1}}}{2} = 18cm\\ \Rightarrow 2{\rm{Asin}}\dfrac{{\omega \Delta {t_1}}}{2} = 2 \Leftrightarrow {\rm{sin}}\dfrac{{\omega \Delta {t_1}}}{2} = \dfrac{1}{4}\\ \Rightarrow \dfrac{{\omega \Delta {t_1}}}{2} = 0,08\pi \Rightarrow \Delta {t_1} = 0,08T\end{array}\) \(\begin{array}{l} \Rightarrow {t_1} = T + \Delta {t_1} = {\rm{ }}T{\rm{ }} + {\rm{ }}0,08T{\rm{ }} = {\rm{ }}3,2s\\ \Rightarrow T = 2,96s\end{array}\) \(t_2= 2,3s = 1,48 + 0,82 = T/2 + 0,82s\) Quãng đường nhỏ nhất vật đi được trong khoảng thời gian \(2,3s\) là: \(\begin{array}{l}{S_{Min}} = 2A + 2A(1 - c{\rm{os}}\dfrac{{\omega \Delta {t_2}}}{2})\\ = 2A + 2A(1 - c{\rm{os}}\dfrac{{\dfrac{{2\pi }}{T}0,82}}{2})\\ = 2.4 + 2.4\left( {1 - c{\rm{os}}\dfrac{{\dfrac{{2\pi }}{{2,96}}.0,82}}{2}} \right) = 10,84cm\end{array}\) Chú ý
Các công thức xác định Smax, Smin dùng trong trường hợp ∆t ≤ T/2
Câu 13 :
Một vật dao động điều hòa với biên độ $10 cm$, tần số góc $2\pi \left( {rad/s} \right)$. Thời gian ngắn nhất để vật đi được quãng đường $16,2 cm$.
Đáp án : B Phương pháp giải :
Áp dụng công thức tính quãng đường lớn nhất: \({S_{{\rm{max}}}} = 2{\rm{Asin}}\frac{{\omega \Delta t}}{2}\) Lời giải chi tiết :
Thời gian ngắn nhất để vật đi được quãng đường S = 16,2 cm = Smax Ta có: \(\begin{array}{l}{S_{{\rm{max}}}} = 2{\rm{Asin}}\frac{{\omega \Delta t}}{2} = 16,2 \to \sin \frac{{\omega \Delta t}}{2} = \frac{{16,2}}{{2.10}} = 0,81\\ \to \frac{{\omega \Delta t}}{2} = 0,3\pi \to \Delta t = \frac{{0,6\pi }}{{2\pi }} = 0,3{\rm{s}}\end{array}\)
Câu 14 :
Một vật dao động điều hòa với biên độ $10 cm$, tần số góc \(2\pi ra{\rm{d}}/s\). Thời gian dài nhất để vật đi được quãng đường $16,2 cm.$
Đáp án : D Phương pháp giải :
Áp dụng công thức tính quãng đường lớn nhất: \({S_{Min}} = 2A(1 - c{\rm{os}}\frac{{\Delta \varphi }}{2})\) Lời giải chi tiết :
Thời gian dài nhất khi $S$ đối xứng qua vị trí biên hay quãng đường đi được là $S_{min}$ 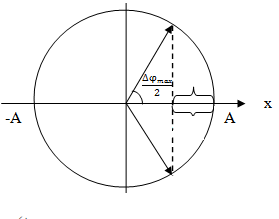 Thời gian dài nhất để vật đi được quãng đường $S = 16,2 cm = S_{min}$ Ta có: \(\begin{array}{l}{S_{Min}} = 2A(1 - c{\rm{os}}\frac{{\Delta \varphi }}{2}) = 16,2 \to c{\rm{os}}\frac{{\Delta \varphi }}{2} = 0,19 \to \frac{{\Delta \varphi }}{2} = 0,44\pi \\ \to \Delta \varphi = \omega \Delta t = 0,88\pi \to \Delta t = 0,44{\rm{s}}\end{array}\)
Câu 15 :
Một vật dao động điều hòa với biên độ $A$, chu kì $T$. Tốc độ trung bình của vật trong một chu kì là:
Đáp án : C Phương pháp giải :
+ Xác định quãng đường vật đi được trong 1 chu kì + Áp dụng công thức tính tốc độ trung bình : \({v_{tb}} = \dfrac{S}{t}\) Lời giải chi tiết :
Ta có : + Quãng đường vật đi được trong $1$ chu kì là $4T$ + Tốc độ trung bình của vật : \({v_{tb}} = \dfrac{S}{t} = \dfrac{{4{\rm{A}}}}{T}\)
Câu 16 :
Một vật dao động điều hòa có độ lớn vận tốc cực đại là $31,4 cm/s$. Lấy $\pi = 3,14$. Tốc độ trung bình của vật trong một chu kì dao động là:
Đáp án : A Phương pháp giải :
+ Sử dụng công thức : vmax = Aω + Áp dụng công thức tính tốc độ trung bình của vật trong 1 chu kì : \({v_{tb}} = \dfrac{{4A}}{T}\) Lời giải chi tiết :
Ta có : vmax = Aω = 31,4 cm/s + Tốc độ trung bình của vật : \({v_{tb}} = \dfrac{S}{t} = \dfrac{{4{\rm{A}}}}{T} = \dfrac{{4\dfrac{{{v_{{\rm{max}}}}}}{\omega }}}{{\dfrac{{2\pi }}{\omega }}} = \dfrac{{4{v_{{\rm{max}}}}}}{{2\pi }} = \dfrac{{4.31,4}}{{2\pi }} = 20cm/s\)
Câu 17 :
Vật dao động điều hoà theo phương trình $x = 5\cos \left( {2\pi t - \frac{\pi }{4}} \right)cm$. Tốc độ trung bình của vật đi được trong khoảng thời gian từ ${t_1} = 1s$ đến ${t_2} = 4,625s$ là:
Đáp án : D Phương pháp giải :
+ Áp dụng công thức tính chu kì dao động: \(T = \dfrac{{2\pi }}{\omega }\) + Xác định (x,v) tại thời điểm t bằng cách thay t vào phương trình + Sử dụng vòng tròn lượng giác được suy ra từ vòng tròn + Áp dụng công thức tính tốc độ trung bình: \({v_{tb}} = \dfrac{S}{{\Delta t}}\) Lời giải chi tiết :
Chu kì dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1{\rm{s}}\) Tại t = 1s: \(\left\{ \begin{array}{l}x = 5c{\rm{os}}\left( {2\pi .1 - \dfrac{\pi }{4}} \right) = 2,5\sqrt 2 \\v = - A\omega \sin \left( {2\pi .1 - \dfrac{\pi }{4}} \right) > 0\end{array} \right.\) Tại t = 4,625s: \(\left\{ \begin{array}{l}x = 5c{\rm{os}}\left( {2\pi .4,625 - \dfrac{\pi }{4}} \right) = - 5\\v = - A\omega \sin \left( {2\pi .4,625 - \dfrac{\pi }{4}} \right) = 0\end{array} \right.\) Khoảng thời gian: \(\Delta t = 3,625{\rm{s}} = 3T + \dfrac{T}{2} + \dfrac{T}{8}\) Quãng đường S trong khoảng thời gian đó: \(S = 3.4A + 2A + \left( {A - \dfrac{{A\sqrt 2 }}{2}} \right) = 15A - \dfrac{{A\sqrt 2 }}{2} = 71,464cm\) Tốc độ trung bình vật đi được trong khoảng thời gian đó là: \({v_{tb}} = \dfrac{S}{{\Delta t}} = \dfrac{{71,464}}{{3,625}} = 19,71cm/s\) 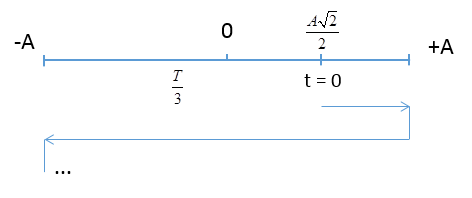
Câu 18 :
Một vật dao động điều hòa có phương trình $x = 5c{\rm{os}}\left( {4\pi t + \frac{\pi }{3}} \right)\left( {cm,s} \right)$. Tốc độ trung bình của vật trong khoảng thời gian tính từ lúc bắt đầu khảo sát dao động đến thời điểm vật đi qua vị trí cân bằng theo chiều dương lần thứ nhất là:
Đáp án : B Phương pháp giải :
+ Sử dụng công thức tính chu kì dao động: \(T = \dfrac{{2\pi }}{\omega }\) + Xác định vị trí tại $t = 0 (x,v)$ + Xác định quãng đường vật đi được + Sử dụng công thức tính tốc độ trung bình: \({v_{tb}} = \dfrac{S}{t}\) Lời giải chi tiết :
Chu kì \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\) $t = 0$: \(\left\{ \begin{array}{l}x = 2,5\\v < 0\end{array} \right.\) Theo hình vẽ: \(\Delta t = \dfrac{T}{{12}} + \dfrac{T}{4} + \dfrac{T}{4} = \dfrac{{7T}}{{12}} = \dfrac{7}{{24}}s\) $S = 2,5+ 5.2 = 12,5 cm$ Tốc độ trung bình: \({v_{tb}} = \dfrac{S}{t} = \dfrac{{12,5}}{{\dfrac{7}{{24}}}} = 42,86cm/s\) 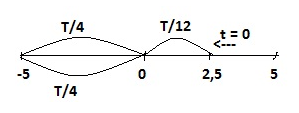
Câu 19 :
Một chất điểm đang dao động với phương trình: $x = 6\cos \left( {10\pi t} \right)cm$. Tính tốc độ trung bình của chất điểm sau $1/4$ chu kì tính từ khi bắt đầu dao động và tốc độ trung bình sau nhiều chu kỳ dao động:
Đáp án : C Phương pháp giải :
+ Áp dụng công thứ xác định chu kì dao động: \(T = \frac{{2\pi }}{\omega }\) + Áp dụng biểu thức xác định tốc độ trung bình: \({v_{TB}} = \frac{S}{t}\) Lời giải chi tiết :
Ta có: A = 6cm, chu kì dao động \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{10\pi }} = 0,2{\rm{s}}\) Tại thời điểm ban đầu t = 0: chất điểm đang ở biên dương +A => Tốc độ trung bình của chất điểm sau 1/4 chu kì là: \({v_{TB}} = \frac{S}{t} = \frac{A}{{\frac{T}{4}}} = \frac{{4A}}{T} = \frac{{4.6}}{{0,2}} = 120cm/s = 1,2m/s\) Cứ 1 chu kì vật đi được quãng đường S = 4A => n chu kì vật đi được quãng đường Sn = n4A => Tốc độ trung bình của chất điểm sau n chu kì là: \({v_{TB}} = \frac{{{S_n}}}{{{t_n}}} = \frac{{4nA}}{{nT}} = \frac{{4A}}{T} = \frac{{4.6}}{{0,2}} = 120cm/s = 1,2m/s\)
Câu 20 :
Một vật nhỏ dao động điều hòa trên đoạn thẳng dài L, chu kỳ T. Quãng đường lớn nhất vật đi được trong khoảng thời gian\(\dfrac{{5T}}{3}\) là
Đáp án : A Phương pháp giải :
Chiều dài quỹ đạo: \(L = 2A\) Quãng đường lớn nhất vật đi được trong thời gian \(t > \dfrac{T}{2}\): \({S_{\max }} = m.2A + 2A\sin \dfrac{{\Delta \varphi }}{2}\) với \(t = m.\dfrac{T}{2} + \Delta t\) Góc quay của vecto quay trong thời gian \(\Delta t\): \(\Delta \varphi = \dfrac{{2\pi }}{T}.\Delta t\) Lời giải chi tiết :
Chiều dài quỹ đạo là: \(L = 2A \Rightarrow A = \dfrac{L}{2}\) Ta có: \(\dfrac{{5T}}{3} = 3.\dfrac{T}{2} + \dfrac{T}{6}\) Trong khoảng thời gian \(\dfrac{T}{6}\), vecto quay được góc: \(\Delta \varphi = \dfrac{{2\pi }}{T}.\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{6} = \dfrac{\pi }{3}\,\,\left( {rad} \right)\) Quãng đường lớn nhất vật đi được trong khoảng thời gian \(\dfrac{{5T}}{3}\) là: \({S_{\max }} = m.2A + 2A\sin \dfrac{{\Delta \varphi }}{2} = 3.2.A + 2A.\sin \dfrac{\pi }{6} = 7A = 3,5L\)
Câu 21 :
Một vật dao động điều hòa với biên độ $A$ và chu kỳ $T$. Tìm tốc độ trung bình nhỏ nhất của vật trong $T/3$?
Đáp án : B Phương pháp giải :
+ Áp dụng công thức tính quãng đường nhỏ nhất: \({S_{Min}} = 2A(1 - c{\rm{os}}\dfrac{{\Delta \varphi }}{2})\) + Áp dụng công thức tính tốc độ trung bình: \({v_{TB}} = \dfrac{S}{t}\) Lời giải chi tiết :
Tốc độ trung bình nhỏ nhất => Quãng đường đi được ngắn nhất \({S_{Min}} = 2A(1 - c{\rm{os}}\dfrac{{\Delta \varphi }}{2}) = 2A(1 - c{\rm{os}}\dfrac{{\dfrac{{2\pi }}{T}.\dfrac{T}{3}}}{2}) = 2A(1 - c{\rm{os}}\dfrac{\pi }{3}) = A\) Tốc độ trung bình của vật trong T/3 là: \({v_{TB}} = \dfrac{S}{t} = \dfrac{A}{{\dfrac{T}{3}}} = \dfrac{{3A}}{T}\)
Câu 22 :
Vật đang dao động điều hòa dọc theo đường thẳng. Một điểm $M$ nằm trên đường thẳng đó, phía ngoài khoảng chuyển động của vật, tại thời điểm t thì vật xa điểm $M$ nhất, sau đó một khoảng thời gian ngắn nhất là $\Delta t$ thì vật gần điểm $M$ nhất. Độ lớn vận tốc của vật sẽ đạt được cực đại vào thời điểm:
Đáp án : A Phương pháp giải :
Sử dụng trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Giả sử điểm M nằm phía ngoài gần biên dương Ta có, tại thời điểm t vật đang ở biên âm Tại t + ∆t: vật đang ở biên dương => ∆t là khoảng thời gian vật đi từ biên âm đến biên dương \( \to \Delta t = \frac{T}{2}\) Độ lớn vận tốc của vật đạt cực đại khi vật ở vị trí cân bằng => Độ lớn vận tốc của vật sẽ đạt được cực đại vào thời điểm: \(t + \frac{{\Delta t}}{2}\) 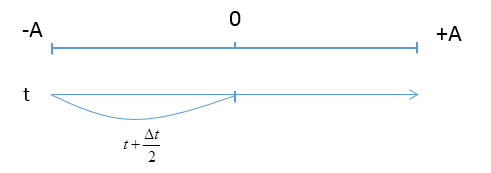
Câu 23 :
Một chất điểm dao động điều hòa với chu kì $T$. Trong khoảng thời gian ngắn nhất khi đi từ vị trí biên có li độ $x = A$ đến vị trí $x = - \dfrac{A}{2}$, chất điểm có tốc độ trung bình là:
Đáp án : B Phương pháp giải :
+ Sử dụng trục thời gian suy ra từ vòng tròn + Áp dụng biểu thức xác định tốc độ trung bình của vật: \({v_{TB}} = \dfrac{S}{{\Delta t}}\) Lời giải chi tiết :
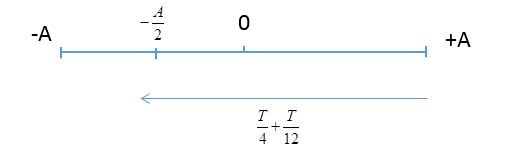 Khoảng thời gian ngắn nhất khi đi từ vị trí $A$ đến $- A/2$ là: \(\Delta t = \dfrac{T}{4} + \dfrac{T}{{12}} = \dfrac{T}{3}\) Quãng đường đi được khi đi từ vị trí $A$ đến $- A/2$ là: \(S = \dfrac{{3A}}{2}\) => Tốc độ trung bình của chất điểm khi đi từ vị trí $A$ đến $- A/2$ là: \({v_{TB}} = \dfrac{S}{{\Delta t}} = \dfrac{{\dfrac{{3A}}{2}}}{{\dfrac{T}{3}}} = \dfrac{{9A}}{{2T}}\)
Câu 24 :
Một vật dao động điều hòa trên trục Ox theo phương trình \(x = A\cos \left( {\dfrac{\pi }{3}t + \varphi } \right)\) ( t tính bằng giây). Trong ba khoảng thời gian theo thứ tự liên tiếp là \(\Delta t = 1s;\Delta {t_2} = \Delta {t_3} = 2s\) thì quãng đường chuyển động của vật lần lượt là \({S_1} = 5cm;{S_2} = 15cm\) và quãng đường S3. Quãng đường S3 gần nhất với giá trị nào sau đây:
Đáp án : B Phương pháp giải :
Sử dụng vòng tròn lượng giác trong dao động điều hòa Lời giải chi tiết :
Ta có: \(T = \dfrac{{2\pi }}{\omega } = 6s \\\to \left\{ \begin{array}{l}\Delta {t_1} + \Delta {t_2} = \dfrac{T}{2}\\{S_1} + {S_2} = 2A = 20cm\end{array} \right. \\\to A = 10cm \\\to \left\{ \begin{array}{l}\Delta {t_1} = 1s = \dfrac{T}{6}\\{S_1} = 5cm = \dfrac{A}{2}\end{array} \right.\) Suy ra vật xuất phát từ 2 biên ( giá sử từ biên dương) , vậy \(\Delta {t_2} = \Delta {t_3} = 2s = \dfrac{T}{3} \to {S_2} = {S_3} = 15cm\)
|



















Danh sách bình luận