Trắc nghiệm: Ôn tập chương 2 Toán 4Đề bài
Câu 1 : Con hãy chọn đáp án đúng nhất
Chọn đáp án đúng nhất. Công thức tìm số lớn khi biết tổng và hiệu của hai số đó là: A. Số lớn = (Tổng – Hiệu) \(:\,2\) B. Số lớn = (Tổng + Hiệu) \(:\,2\) C. Số lớn = (Tổng + Hiệu) \( \times \,2\) D. Số lớn = (Tổng – Hiệu) \( \times \,2\)
Câu 2 : Con hãy lựa chọn đáp án Đúng hoặc Sai
Khi nhân số tự nhiên với $10,{\rm{ }}100,{\rm{ }}1000,\,\,...$ ta chỉ việc viết thêm một, hai, ba ... chữ số \(0\) vào bên phải số đó. Đúng hay sai? Đúng Sai
Câu 3 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: \(24{m^2}\,\,5d{m^2}\,\, =\) $dm^2$.
Câu 4 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: Phép tính \(24657 + 43575\) có kết quả là
Câu 5 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Tính nhẩm: \(72 \times 11=\)
Câu 6 : Con hãy chọn đáp án đúng nhất
Nếu $a = 25,{\rm{ }}b = 78$ thì giá trị của biểu thức $\left( {375 + 3450} \right):{\rm{a}} + 412 \times b$ là: A. \(32289\) B. \(32749\) C. \(44070\) D. \(72150\)
Câu 7 : Con hãy chọn đáp án đúng nhất
Hình dưới đây có bao nhiêu góc nhọn, bao nhiêu góc tù, bao nhiêu góc bẹt? 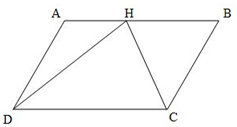 A. Hình đã cho có \(8\) góc nhọn, \(3\) góc tù, \(1\) góc bẹt. B. Hình đã cho có \(8\) góc nhọn, \(4\) góc tù, \(1\) góc bẹt. C. Hình đã cho có \(9\) góc nhọn, \(3\) góc tù, \(1\) góc bẹt. D. Hình đã cho có \(9\) góc nhọn, \(4\) góc tù, \(1\) góc bẹt.
Câu 8 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: Một tổ sản xuất làm trong hai ngày được \(2578\) sản phẩm, ngày thứ hai sản xuất được nhiều hơn ngày thứ nhất \(164\) sản phẩm. Vậy ngày thứ nhất tổ đó sản xuất được sản phẩm, ngày thứ hai tổ đó sản xuất được sản phẩm.
Câu 9 : Con hãy chọn đáp án đúng nhất
Tìm \(x\), biết: \(38766:(x - 78) = 182\) A. \(x = 295\) B. \(x = 291\) C. \(x = 278\) D. \(x = 135\)
Câu 10 : Con hãy chọn đáp án đúng nhất
Tìm \(y\) , biết: $18 \times y + 27 \times y = 31048 - 20383$ A. $y = 233$ B. $y = 235$ C. $y = 237$ D. $y = 239$
Câu 11 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: Một kho chứa \(464\) bao xi măng, mỗi bao cân nặng \(50kg\). Người ta đã lấy đi \(\dfrac{1}{8}\) số xi măng đó. Vậy trong kho còn lại tạ xi măng.
Câu 12 : Con hãy chọn đáp án đúng nhất
Một mảnh vườn hình chữ nhật có chu vi là $112m$, chiều dài hơn chiều rộng \(16m\). Người ta trồng dâu tây trên mảnh vườn đó, cứ \(1{m^2}\) thu được $2kg$ dâu tây. Mỗi ki-lô-gam dâu tây bán với giá $75\,\,000$ đồng. Hỏi trên cả mảnh vườn đó thu được tất cả bao nhiêu tiền? A. \(108\,\,000\,\,000\) đồng B. \(118\,\,000\,\,000\) đồng C. \(248\,\,300\,\,000\) đồng D. \(460\,\,800\,\,000\) đồng
Câu 13 : Con hãy chọn đáp án đúng nhất
Khi chia \(74024\) cho một số tự nhiên thì có số dư là $234$ và đó là số dư lớn nhất có thể có trong phép chia này. Tìm số chia và thương của phép chia đó. A. Số chia: \(236\); thương : \(312\) B. Số chia: \(235\); thương : \(312\) C. Số chia: \(236\); thương : \(314\) D. Số chia: \(235\); thương : \(314\)
Câu 14 : Con hãy chọn đáp án đúng nhất
Trung bình cộng số tuổi của bố, Hoa và Huy là \(20\) tuổi. Tuổi bố hơn tổng số tuổi của Hoa và Huy là \(20\) tuổi, Hoa kém Huy \(4\) tuổi. Tính tuổi của mỗi người. A. Bố: \(39\) tuổi; Hoa: \(9\) tuổi; Huy: \(13\) tuổi B. Bố: \(40\) tuổi; Hoa: \(8\) tuổi; Huy: \(12\) tuổi C. Bố: \(42\) tuổi; Hoa: \(7\) tuổi; Huy: \(11\) tuổi D. Bố: \(44\) tuổi; Hoa: \(6\) tuổi; Huy: \(10\) tuổi Lời giải và đáp án
Câu 1 : Con hãy chọn đáp án đúng nhất
Chọn đáp án đúng nhất. Công thức tìm số lớn khi biết tổng và hiệu của hai số đó là: A. Số lớn = (Tổng – Hiệu) \(:\,2\) B. Số lớn = (Tổng + Hiệu) \(:\,2\) C. Số lớn = (Tổng + Hiệu) \( \times \,2\) D. Số lớn = (Tổng – Hiệu) \( \times \,2\) Đáp án
B. Số lớn = (Tổng + Hiệu) \(:\,2\) Phương pháp giải :
Xem lại lí thuyết phần tìm hai số khi biết tổng và hiệu của hai số đó. Lời giải chi tiết :
Công thức tìm hai số khi biết tổng và hiệu của hai số đó là: Số lớn = (Tổng + Hiệu) \(:\,\,2\) ; Số bé = (Tổng + Hiệu) \(:\,\,2\) Vậy đáp án đúng là: Số lớn = (Tổng + Hiệu) \(:\,\,2\).
Câu 2 : Con hãy lựa chọn đáp án Đúng hoặc Sai
Khi nhân số tự nhiên với $10,{\rm{ }}100,{\rm{ }}1000,\,\,...$ ta chỉ việc viết thêm một, hai, ba ... chữ số \(0\) vào bên phải số đó. Đúng hay sai? Đúng Sai Đáp án
Đúng Sai Phương pháp giải :
Xem lại lí thuyết về cách nhân số tự nhiên với $10,{\rm{ }}100,{\rm{ }}1000,\,\,...$ Lời giải chi tiết :
Khi nhân số tự nhiên với $10,{\rm{ }}100,{\rm{ }}1000,\,\,...$ ta chỉ việc viết thêm một, hai, ba ... chữ số \(0\) vào bên phải số đó.
Câu 3 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: \(24{m^2}\,\,5d{m^2}\,\, =\) $dm^2$. Đáp án
\(24{m^2}\,\,5d{m^2}\,\, =\) $dm^2$. Phương pháp giải :
Áp dụng tính chất: \(1{m^2} = 100d{m^2}\) để đổi \(24{m^2}\) sang đơn vị \(d{m^2}\), sau đó cộng thêm với \(5d{m^2}\). Lời giải chi tiết :
Ta có:
Câu 4 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: Phép tính \(24657 + 43575\) có kết quả là Đáp án
Phép tính \(24657 + 43575\) có kết quả là Phương pháp giải :
Muốn cộng hai số tự nhiên ta có thể làm như sau: - Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau. - Cộng các chữ số ở từng hàng theo thứ tự từ phải sang trái, tức là từ hàng đơn vị đến hàng chục, hàng trăm, hàng nghìn, … . Lời giải chi tiết :
Đặt tính và thực hiện tính ta có:
Câu 5 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Tính nhẩm: \(72 \times 11=\) Đáp án
Tính nhẩm: \(72 \times 11=\) Phương pháp giải :
Áp dụng cách nhân nhẩm với \(11:\) Muốn nhân nhẩm một số có hai chữ số với \(11\) ta lấy chữ số hàng chục cộng với chữ số hàng đơn vị, nếu tổng tìm được bé hơn \(10\) thì ta viết tổng vào giữa hai chữ số đã cho. Lời giải chi tiết :
Cách nhẩm: +) \(7\) cộng $2$ bằng \(9\) +) Viết \(9\) vào giữa hai chữ số của $72$, được $792$. Vậy ta có: \(72 \times 11 = 792\) . Đáp án đúng điền vào ô trống là \(792\).
Câu 6 : Con hãy chọn đáp án đúng nhất
Nếu $a = 25,{\rm{ }}b = 78$ thì giá trị của biểu thức $\left( {375 + 3450} \right):{\rm{a}} + 412 \times b$ là: A. \(32289\) B. \(32749\) C. \(44070\) D. \(72150\) Đáp án
A. \(32289\) Phương pháp giải :
- Thay $a = 25,{\rm{ }}b = 78$ vào biểu thức đã cho rồi tính giá trị biểu thức đó. - Biểu thức có chứa dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau. - Biểu thức có phép cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước; phép cộng, trừ sau. Lời giải chi tiết :
Nếu $a = 25,{\rm{ }}b = 78$ thì: $\left( {375 + 3450} \right):{\rm{ a}} + {\rm{ }}412 \times b $ $= (375 + 3450):25 + 412 \times 78$ $ = 3825:25 + 32136 $ $= 153 + 32136$ $= 32289$ Vậy với $a = 25,{\rm{ }}b = 78$ thì giá trị của biểu thức $\left( {375 + 3450} \right):{\rm{ a}} + {\rm{ }}412 \times b$ là \(32289\).
Câu 7 : Con hãy chọn đáp án đúng nhất
Hình dưới đây có bao nhiêu góc nhọn, bao nhiêu góc tù, bao nhiêu góc bẹt? A. Hình đã cho có \(8\) góc nhọn, \(3\) góc tù, \(1\) góc bẹt. B. Hình đã cho có \(8\) góc nhọn, \(4\) góc tù, \(1\) góc bẹt. C. Hình đã cho có \(9\) góc nhọn, \(3\) góc tù, \(1\) góc bẹt. D. Hình đã cho có \(9\) góc nhọn, \(4\) góc tù, \(1\) góc bẹt. Đáp án
D. Hình đã cho có \(9\) góc nhọn, \(4\) góc tù, \(1\) góc bẹt. Phương pháp giải :
Quan sát hình vẽ để xác định các góc. Lời giải chi tiết :
Trong hình đã cho có: - \(9\) góc nhọn: + Góc nhọn đỉnh H; cạnh HA và HD. + Góc nhọn đỉnh H; cạnh HC và HD. + Góc nhọn đỉnh B; cạnh BA và BC. + Góc nhọn đỉnh C; cạnh CB và CH. + Góc nhọn đỉnh C; cạnh CH và CD . + Góc nhọn đỉnh D; cạnh DH và DC. + Góc nhọn đỉnh D; cạnh DA và DH. + Góc nhọn đỉnh D; cạnh DA và DC. - \(4\) góc tù: + Góc tù đỉnh A; cạnh AD và AB. + Góc tù đỉnh H; cạnh HA và HC. + Góc tù đỉnh H; cạnh HB và HD. + Góc tù đỉnh C; cạnh CB và CD. - \(1\) góc tù: + Góc tù đỉnh H; cạnh HC và HC. Vậy hình đã cho có \(9\) góc nhọn; \(4\) góc tù, \(1\) góc bẹt.
Câu 8 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: Một tổ sản xuất làm trong hai ngày được \(2578\) sản phẩm, ngày thứ hai sản xuất được nhiều hơn ngày thứ nhất \(164\) sản phẩm. Vậy ngày thứ nhất tổ đó sản xuất được sản phẩm, ngày thứ hai tổ đó sản xuất được sản phẩm. Đáp án
Một tổ sản xuất làm trong hai ngày được \(2578\) sản phẩm, ngày thứ hai sản xuất được nhiều hơn ngày thứ nhất \(164\) sản phẩm. Vậy ngày thứ nhất tổ đó sản xuất được sản phẩm, ngày thứ hai tổ đó sản xuất được sản phẩm. Phương pháp giải :
Áp dụng công thức tìm hai số khi biết tổng và hiệu của hai số đó: Số bé = (tổng – hiệu) : $2$; Số lớn = (tổng + hiệu) : $2$. Lời giải chi tiết :
Ta có sơ đồ: 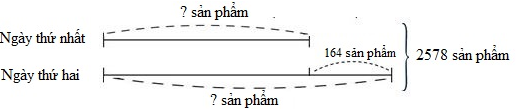 Ngày thứ nhất tổ đó sản xuất được số sản phẩm là: \((2578 - 164):2 = 1207\) (sản phẩm) Ngày thứ hai tổ đó sản xuất được số sản phẩm là: \(2578 - 1207 = 1371\) (sản phẩm) Đáp số: Ngày thứ nhất: \(1207\) sản phẩm Ngày thứ hai: \(1371\) sản phẩm Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(1207\,;\,\,1371\).
Câu 9 : Con hãy chọn đáp án đúng nhất
Tìm \(x\), biết: \(38766:(x - 78) = 182\) A. \(x = 295\) B. \(x = 291\) C. \(x = 278\) D. \(x = 135\) Đáp án
B. \(x = 291\) Phương pháp giải :
+) \(x - 78\) ở vị trí số chia, muốn tìm số chia ta lấy số bị chia chia cho thương. +) \(x\) ở vị trí số bị trừ, muốn tìm số bị trừ ta lấy hiệu cộng với số trừ. Lời giải chi tiết :
\(\begin{array}{l}38766:(x - 78) = 182\\x - 78 = 38766:182\\x - 78 = 213\\x =213+78\\ x = 291\end{array}\) Vậy đáp án đúng là \(x = 291\).
Câu 10 : Con hãy chọn đáp án đúng nhất
Tìm \(y\) , biết: $18 \times y + 27 \times y = 31048 - 20383$ A. $y = 233$ B. $y = 235$ C. $y = 237$ D. $y = 239$ Đáp án
C. $y = 237$ Phương pháp giải :
- Viết biểu thức bên trái dấu bằng về dạng một tổng nhân với một số. - Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết. Lời giải chi tiết :
$18 \times y + 27 \times y = 31048 - 20383\;$ $(18 + 27) \times y = 31048 - 20383\;$ $45 \times y = 10665$ $y = 10665:45$ $y = 237$ Vậy đáp án đúng là $y = 237$.
Câu 11 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: Một kho chứa \(464\) bao xi măng, mỗi bao cân nặng \(50kg\). Người ta đã lấy đi \(\dfrac{1}{8}\) số xi măng đó. Vậy trong kho còn lại tạ xi măng. Đáp án
Một kho chứa \(464\) bao xi măng, mỗi bao cân nặng \(50kg\). Người ta đã lấy đi \(\dfrac{1}{8}\) số xi măng đó. Vậy trong kho còn lại tạ xi măng. Phương pháp giải :
- Tìm khối lượng xi măng có trong kho lúc đầu ta lấy cân nặng của một bao nhân với số bao. - Tìm khối lượng xi măng đã lấy đi tức là ta tìm \(\dfrac{1}{8}\) của tổng khối lượng xi măng, hay ta lấy tổng khối lượng xi măng chia cho \(8\). - Tìm khối lượng xi măng còn lại ta lấy khối lượng xi măng có trong kho lúc đầu trừ đi khối lượng xi măng đã lấy đi. - Đổi số đo vừa tìm được sang đơn vị tạ. Lời giải chi tiết :
Kho đó có tất cả số ki-lô-gam xi măng là: \(50 \times 464 = 23200\,\,(kg)\) Người ta đã lấy đi số ki-lô-gam xi măng là: \(23200:8 = 2900\,\,(kg)\) Trong kho còn lại số ki-lô-gam xi măng là: \(23200 - 2900 = 20300\,\,(kg)\) \(20300kg = 203\) tạ Đáp số: \(203\) tạ. Vậy đáp án đúng điền vào ô trống là \(203\).
Câu 12 : Con hãy chọn đáp án đúng nhất
Một mảnh vườn hình chữ nhật có chu vi là $112m$, chiều dài hơn chiều rộng \(16m\). Người ta trồng dâu tây trên mảnh vườn đó, cứ \(1{m^2}\) thu được $2kg$ dâu tây. Mỗi ki-lô-gam dâu tây bán với giá $75\,\,000$ đồng. Hỏi trên cả mảnh vườn đó thu được tất cả bao nhiêu tiền? A. \(108\,\,000\,\,000\) đồng B. \(118\,\,000\,\,000\) đồng C. \(248\,\,300\,\,000\) đồng D. \(460\,\,800\,\,000\) đồng Đáp án
A. \(108\,\,000\,\,000\) đồng Phương pháp giải :
- Tính nửa chu vi: Nửa chu vi \(=\) chu vi \(:\,2= \) chiều dài \(+\) chiều rộng. - Tìm chiều dài và chiều rộng dựa vào công thức tìm hai số khi biết tổng và hiệu của hai số : Số bé = (tổng – hiệu) : $2$; Số lớn = (tổng + hiệu) : $2$. - Tính diện tích = chiều dài × chiều rộng. - Tính khối lượng dâu tây thu được ta lấy số dâu tây thu hoạch được trên \(1{m^2}\) nhân với diện tích mảnh vườn. - Tính số tiền thu được ta lấy giá bán của \(1kg\) nhân với khối lượng dâu tây thu được. Lời giải chi tiết :
Nửa chu vi mảnh vườn là: $112:2 = 56\,\,(m)$ Chiều rộng của mảnh vườn hình chữ nhật đó là: \((56 - 16):2 = 20\,(m)\) Chiều dài của mảnh vườn hình chữ nhật đó là: \(20 + 16 = 36\,\,(m)\) Diện tích của mảnh vườn hình chữ nhật đó là: \(36\, \times 20 = 720\,\,({m^2})\) Trên cả mảnh vườn đó người ta thu được số ki-lô-gam dâu tây là: \(720 \times 2 = 1440\,(kg)\) Trên cả mảnh vườn đó người ta thu được số tiền là \(75\,\,000 \times 1440 = \,\,\,108\,\,000\,\,000\) (đồng) Đáp số: \(108\,\,000\,\,000\) đồng.
Câu 13 : Con hãy chọn đáp án đúng nhất
Khi chia \(74024\) cho một số tự nhiên thì có số dư là $234$ và đó là số dư lớn nhất có thể có trong phép chia này. Tìm số chia và thương của phép chia đó. A. Số chia: \(236\); thương : \(312\) B. Số chia: \(235\); thương : \(312\) C. Số chia: \(236\); thương : \(314\) D. Số chia: \(235\); thương : \(314\) Đáp án
D. Số chia: \(235\); thương : \(314\) Phương pháp giải :
- Trong phép chia có dư, số dư lớn nhất trong phép chia đó sẽ kém số chia \(1\) đơn vị. Từ đó ta tìm được số chia. - Từ công thức: Số bị chia = thương \( \times \) số chia + số dư, ta tìm thương bằng cách lấy hiệu của số bị chia và số dư chia cho số chia. Lời giải chi tiết :
Vì $234$ là số dư lớn nhất có thể có trong phép chia này nên số chia của phép chia này là: $234 + 1 = 235$ Gọi \(a\) là thương của phép chia đó. Theo đề bài ta có: $74024:235 = a$ (dư \(234\)) \(\begin{array}{l}a = (74024 - 234):235\\a = 73790:235\\a = 314\end{array}\) Vậy số chia của phép chia đó là \(235\), thương là \(314\).
Câu 14 : Con hãy chọn đáp án đúng nhất
Trung bình cộng số tuổi của bố, Hoa và Huy là \(20\) tuổi. Tuổi bố hơn tổng số tuổi của Hoa và Huy là \(20\) tuổi, Hoa kém Huy \(4\) tuổi. Tính tuổi của mỗi người. A. Bố: \(39\) tuổi; Hoa: \(9\) tuổi; Huy: \(13\) tuổi B. Bố: \(40\) tuổi; Hoa: \(8\) tuổi; Huy: \(12\) tuổi C. Bố: \(42\) tuổi; Hoa: \(7\) tuổi; Huy: \(11\) tuổi D. Bố: \(44\) tuổi; Hoa: \(6\) tuổi; Huy: \(10\) tuổi Đáp án
B. Bố: \(40\) tuổi; Hoa: \(8\) tuổi; Huy: \(12\) tuổi Phương pháp giải :
- Tính tổng số tuổi của ba người ta lấy số tuổi trung bình nhân với \(3\). - Coi tuổi bố là số lớn, tổng số tuổi của Hoa và Huy là số bé. Ta tìm số lớn và số bé theo công thức tìm hai số khi biết tổng và hiệu : Số bé = (tổng – hiệu) : $2$; Số lớn = (tổng + hiệu) : $2$. - Tìm được tổng số tuổi của Hoa và Huy, lại có hiệu số tuổi của 2 người, áp dụng công thức tìm hai số khi biết tổng và hiệu ta tìm được tuổi của mỗi người. Lời giải chi tiết :
Tổng số tuổi của ba người là: \(20 \times 3 = 60\) (tuổi) Tuổi bố là: \((60 + 20):2 = 40\) (tuổi) Tổng số tuổi của Hoa và Huy là: \(60 - 40 = 20\) (tuổi) Tuổi Hoa là: \((20 + 4):2 = 12\) (tuổi) Tuổi Huy là: \(20 - 12 = 8\) (tuổi) Đáp số: Bố: \(40\) tuổi; Hoa: \(8\) tuổi; Huy: \(12\) tuổi.
|
Điền số thích hợp vào ô trống:
