Trắc nghiệm: Hình bình hành – Diện tích hình bình hành Toán 4Đề bài
Câu 1 :
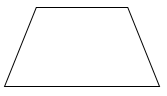
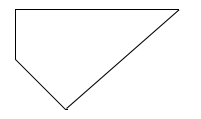
Trong các hình sau, hình nào là hình bình hành?
Câu 2 :
Một hình bình hành có độ dài đáy là \(a\), chiều cao là \(h\). Khi đó công thức tính diện tích hình bình hành đó là: A. \(S = (a + h) \times 2\) \(\) B. \(S = a + h\) C. \(S = a \times h\) D. \(S = a\, \times h:2\)
Câu 3 :
Diện tích hình bình hành có độ dài đáy là \(14cm\) và chiều cao là \(8cm\) là: A. \(22c{m^2}\) B. \(44c{m^2}\) C. \(56c{m^2}\) D. \(112c{m^2}\)
Câu 4 :
Điền số thích hợp vào ô trống:
Cho hình bình hành như hình vẽ:
Diện tích hình bình hành đã cho là \(d{m^2}\).
Câu 5 :
Điền số thích hợp vào ô trống: Hình bình hành có độ dài đáy là \(42dm\) và chiều cao là \(3m\) có diện tích là. \(d{m^2}\).
Câu 6 :
Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\) B. \(17cm\) C. \(18cm\) D. \(19cm\)
Câu 7 :
Hình bình hành ABCD có độ dài cạnh AB là \(a\), độ dài cạnh BC là \(b\).
Công thức tính chu vi P của hình bình hành là: \(P = (a + b) \times 2\) (\(a\) và \(b\) cùng một đơn vị đo) Áp dụng công thức trên để tính chu vi hình bình hành biết \(a = 48cm\) và \(b = 34cm\). A. \(14cm\) B. \(82cm\) C. \(164cm\) D. \(1632cm\)
Câu 8 :
Một khu rừng dạng hình bình hành có chiều cao là \(678m\), độ dài đáy gấp đôi chiều cao. Diện tích khu rừng đó là: A. \(991368{m^2}\) B. \(939148{m^2}\) C. \(919348{m^2}\) D. \(919368{m^2}\)
Câu 9 :
Điền số thích hợp vào ô trống: Một hình bình hành có chiều cao là $27cm$, độ dài đáy gấp \(3\) lần chiều cao. Vậy diện tích hình bình hành đó là \(cm^2\).
Câu 10 :
Điền số thích hợp vào ô trống: Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\). Vậy chiều cao của hình bình hành đó là \(dm\).
Câu 11 :
Điền số thích hợp vào ô trống: Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\). Vậy chiều cao tương ứng với cạnh đáy đó là \(cm\).
Câu 12 :
Một mảnh vườn dạng hình bình hành có tổng độ dài của chiều cao và độ dài đáy là $233m$, chiều cao kém độ dài đáy $17m$. Người ta trồng ngô trên mảnh vườn đó, tính ra cứ 100m2 thì thu được 60kg ngô. Hỏi đã thu hoạch được bao nhiêu tạ ngô trên mảnh vườn đó? A. \(81\) tạ B. \(162\) tạ C. \(8100\) tạ D. \(16\,\,200\) tạ
Câu 13 :
Điền số thích hợp vào ô trống:
Biết hình bình hành ABCD có $AB = 35cm$ và$BC = 30cm$, đường cao $AH = 42cm$. Vậy độ dài đường cao AK tương ứng với cạnh BC là \( cm\).
Câu 14 :
Điền số thích hợp vào ô trống: Một mảnh vườn hình bình hành có độ dài đáy \(145m\), chiều cao kém độ dài đáy \(29m\). Người ta dự định dùng $\dfrac{1}{4}$ diện tích đất để trồng xoài, diện tích còn lại dùng để trồng cam. Vậy diện tích đất trồng cam là \(m^2\). Lời giải và đáp án
Câu 1 :
Trong các hình sau, hình nào là hình bình hành?
Đáp án
Lời giải chi tiết :
Quan sát các hình đã cho ta thấy hình thứ nhất và hình thứ tư từ trên xuống có hai cặp cạnh đối diện song song và bằng nhau nên các hình đó là hình bình hành.
Câu 2 :
Một hình bình hành có độ dài đáy là \(a\), chiều cao là \(h\). Khi đó công thức tính diện tích hình bình hành đó là: A. \(S = (a + h) \times 2\) \(\) B. \(S = a + h\) C. \(S = a \times h\) D. \(S = a\, \times h:2\) Đáp án
C. \(S = a \times h\) Lời giải chi tiết :
Diện tích hình bình hành bằng độ dài đáy nhân với chiều cao (cùng một đơn vị đo). Do đó, bình hành có độ dài đáy là \(a\), chiều cao là \(h\) thì diện tích hình bình hành đó được tính theo công thức: \(S = a \times h\).
Câu 3 :
Diện tích hình bình hành có độ dài đáy là \(14cm\) và chiều cao là \(8cm\) là: A. \(22c{m^2}\) B. \(44c{m^2}\) C. \(56c{m^2}\) D. \(112c{m^2}\) Đáp án
D. \(112c{m^2}\) Phương pháp giải :
Độ dài đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy độ dài đáy nhân với chiều cao. Lời giải chi tiết :
Diện tích hình bình hành đó là: \(14 \times 8 = 112\left( {c{m^2}} \right)\) Đáp số: \(112c{m^2}\).
Câu 4 :
Điền số thích hợp vào ô trống:
Cho hình bình hành như hình vẽ:
Diện tích hình bình hành đã cho là \(d{m^2}\). Đáp án
Cho hình bình hành như hình vẽ:
Diện tích hình bình hành đã cho là \(d{m^2}\). Phương pháp giải :
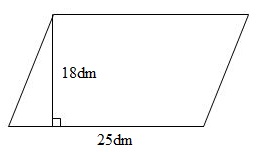
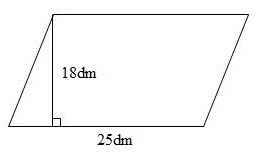
Hình bình hành đã cho có chiều cao là \(18dm\) , độ dài đáy là \(25dm\) . Để tính diện tích ta lấy độ dài đáy nhân với chiều cao Lời giải chi tiết :
Diện tích hình bình hành đó là: \(25 \times 18 = 450\left( {d{m^2}} \right)\) Đáp số: \(450d{m^2}\). Vậy đáp án đúng điền vào ô trống là \(450\).
Câu 5 :
Điền số thích hợp vào ô trống: Hình bình hành có độ dài đáy là \(42dm\) và chiều cao là \(3m\) có diện tích là. \(d{m^2}\). Đáp án
Hình bình hành có độ dài đáy là \(42dm\) và chiều cao là \(3m\) có diện tích là. \(d{m^2}\). Phương pháp giải :
Độ dài đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đo, sau đó để tính diện tích ta lấy độ dài đáy nhân với chiều cao. Lời giải chi tiết :
Đổi \(3m = 30dm\) Diện tích hình bình hành đó là: \(42 \times 30 = 1260\left( {d{m^2}} \right)\) Vậy đáp án đúng điền vào ô trống là \(1260\).
Câu 6 :
Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\) B. \(17cm\) C. \(18cm\) D. \(19cm\) Đáp án
C. \(18cm\) Phương pháp giải :
Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính độ dài cạnh đáy \(a\) là \(a = S:h\). Lời giải chi tiết :
Độ dài đáy của hình bình hành đó là: \(432:24 = 18\,\,(cm)\) Đáp số: \(18cm\).
Câu 7 :
Hình bình hành ABCD có độ dài cạnh AB là \(a\), độ dài cạnh BC là \(b\).
Công thức tính chu vi P của hình bình hành là: \(P = (a + b) \times 2\) (\(a\) và \(b\) cùng một đơn vị đo) Áp dụng công thức trên để tính chu vi hình bình hành biết \(a = 48cm\) và \(b = 34cm\). A. \(14cm\) B. \(82cm\) C. \(164cm\) D. \(1632cm\) Đáp án
C. \(164cm\) Phương pháp giải :
Thay \(a = 48cm\) và \(b = 34cm\) vào biểu thức \(P = (a + b) \times 2\) rồi tính giá trị biểu thức đó. Lời giải chi tiết :
Nếu \(a = 48cm\) và \(b = 34cm\) thì \(P = (a + b) \times 2 = (48 + 34) \times 2 = 164\,\,(cm)\). Vậy chu vi hình bình hành đó là \(164cm\).
Câu 8 :
Một khu rừng dạng hình bình hành có chiều cao là \(678m\), độ dài đáy gấp đôi chiều cao. Diện tích khu rừng đó là: A. \(991368{m^2}\) B. \(939148{m^2}\) C. \(919348{m^2}\) D. \(919368{m^2}\) Đáp án
D. \(919368{m^2}\) Phương pháp giải :
- Tính độ dài đáy ta lấy chiều cao nhân với \(2\). - Tính diện tích khu rừng đó ta lấy độ dài đáy nhân với chiều cao. Lời giải chi tiết :
Độ dài đáy của khu rừng đó là: $678 \times 2 = 1356\,\,(m)$ Diện tích của khu rừng đó là: $678 \times 1356 = 919368\,\,({m^2})$ Đáp số: \(919368{m^2}\).
Câu 9 :
Điền số thích hợp vào ô trống: Một hình bình hành có chiều cao là $27cm$, độ dài đáy gấp \(3\) lần chiều cao. Vậy diện tích hình bình hành đó là \(cm^2\). Đáp án
Một hình bình hành có chiều cao là $27cm$, độ dài đáy gấp \(3\) lần chiều cao. Vậy diện tích hình bình hành đó là \(cm^2\). Phương pháp giải :
Muốn tính được diện tích hình bình hành ta phải biết độ dài đáy và chiều cao. Ta có thể giải như sau: - Tính độ dài đáy ta lấy chiều cao nhân với \(3\). - Tính diện tích ta lấy độ dài đáy nhân với chiều cao. Lời giải chi tiết :
Chiều cao của hình bình hành là: $27 \times 3 = 81\,\,(cm)$ Diện tích của hình bình hành là: $27 \times 81 = 2187\,\,(c{m^2})$ Đáp số: \(2187c{m^2}\). Vậy đáp án đúng điền vào ô trống là \(2187\).
Câu 10 :
Điền số thích hợp vào ô trống: Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\). Vậy chiều cao của hình bình hành đó là \(dm\). Đáp án
Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\). Vậy chiều cao của hình bình hành đó là \(dm\). Phương pháp giải :
Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính chiều cao \(h\) là \(h = S\,\,:\,\,a\). Lời giải chi tiết :
Chiều cao của hình bình hành đó là: \(1855:53 = 35\,\,(dm)\) Đáp số: \(35dm\). Vậy đáp án đúng điền vào ô trống là \(35\).
Câu 11 :
Điền số thích hợp vào ô trống: Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\). Vậy chiều cao tương ứng với cạnh đáy đó là \(cm\). Đáp án
Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\). Vậy chiều cao tương ứng với cạnh đáy đó là \(cm\). Phương pháp giải :
- Đổi \(8d{m^2}\) sang đơn vị đo là \(c{m^2}\). - Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính chiều cao \(h\) là \(h = S\,:\,a\). Lời giải chi tiết :
Đổi \(8d{m^2} = 800c{m^2}\) Chiều cao của hình bình hành đó là: \(800:32 = 25\,\,(cm)\) Đáp số: \(25cm\). Vậy đáp án đúng điền vào ô trống là \(25\).
Câu 12 :
Một mảnh vườn dạng hình bình hành có tổng độ dài của chiều cao và độ dài đáy là $233m$, chiều cao kém độ dài đáy $17m$. Người ta trồng ngô trên mảnh vườn đó, tính ra cứ 100m2 thì thu được 60kg ngô. Hỏi đã thu hoạch được bao nhiêu tạ ngô trên mảnh vườn đó? A. \(81\) tạ B. \(162\) tạ C. \(8100\) tạ D. \(16\,\,200\) tạ Đáp án
A. \(81\) tạ Phương pháp giải :
- Ta có tổng và hiệu của chiều cao và độ dài đáy. Ta sẽ tìm chiều cao và độ dài đáy theo công thức tìm hai số khi biết tổng và hiệu của hai số đó: Số lớn = (Tổng + Hiệu) \(:\,\,2\) ; Số bé = (Tổng – hiệu) \(:\,\,2\) - Tìm diện tích mảnh vườn ta lấy độ dài đáy nhân với chiều cao. - Tìm diện tích mảnh vườn gấp \(100{m^2}\) bao nhiêu lần. - Tìm trên cả mảnh vườn thu hoạch được bao nhiêu ki-lô-gam ngô và đổi sang đơn vị tạ. Lời giải chi tiết :
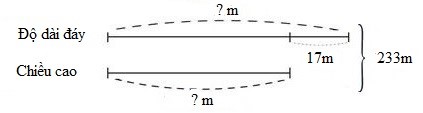
Ta có sơ đồ:
Độ dài đáy của mảnh vườn đó là: \((233 + 17):2 = 125\left( m \right)\) Chiều cao của mảnh vườn đó là: \(125 - 17 = 108\,\,\left( m \right)\) Diện tích mảnh vườn đó là: \(125 \times 108 = 13500\left( {{m^2}} \right)\) \(13500{m^2}\) gấp \(100{m^2}\) số lần là: \(13500:100 = 135\) (lần) Trên cả mảnh vườn đó người ta thu hoạch được số ki-lô-gam ngô là: \(60 \times 135 = 8100\;(kg)\) \(8100kg = 81\) tạ Đáp số: \(81\) tạ.
Câu 13 :
Điền số thích hợp vào ô trống:
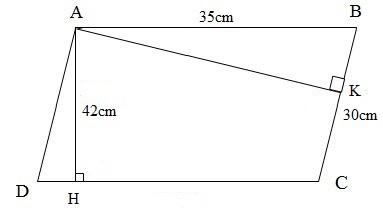
Biết hình bình hành ABCD có $AB = 35cm$ và$BC = 30cm$, đường cao $AH = 42cm$. Vậy độ dài đường cao AK tương ứng với cạnh BC là \( cm\). Đáp án
Biết hình bình hành ABCD có $AB = 35cm$ và$BC = 30cm$, đường cao $AH = 42cm$. Vậy độ dài đường cao AK tương ứng với cạnh BC là \( cm\). Phương pháp giải :
- Tìm độ dài CD: ABCD là hình bình hành nên $AB = CD = 35cm$. - Tính diện tích hình bình hành ABCD ta lấy chiều cao AH nhân với đáy CD. - Tính chiều cao AK ta lấy diện tích chia cho đáy. Lời giải chi tiết :
Vì ABCD là hình bình hành nên $AB = CD = 35cm$. Diện tích hình bình hành đó là: $35 \times 42 = 1470\;\left( {c{m^2}} \right)$ Độ dài đường cao AK là: $1470:30 = 49\;\left( {cm} \right)$ Đáp số: \(49cm\). Vậy đáp án đúng điền vào ô trống là \(49\).
Câu 14 :
Điền số thích hợp vào ô trống: Một mảnh vườn hình bình hành có độ dài đáy \(145m\), chiều cao kém độ dài đáy \(29m\). Người ta dự định dùng $\dfrac{1}{4}$ diện tích đất để trồng xoài, diện tích còn lại dùng để trồng cam. Vậy diện tích đất trồng cam là \(m^2\). Đáp án
Một mảnh vườn hình bình hành có độ dài đáy \(145m\), chiều cao kém độ dài đáy \(29m\). Người ta dự định dùng $\dfrac{1}{4}$ diện tích đất để trồng xoài, diện tích còn lại dùng để trồng cam. Vậy diện tích đất trồng cam là \(m^2\). Phương pháp giải :
- Chiều cao kém độ dài đáy \(29m\)tức là độ dài đáy hơn chiều cao \(29m\). Để tính chiều cao ta lấy độ dài đáy trừ đi \(29m\). - Tính diện tích cả mảnh vườn ta lấy độ dài đáy nhân với chiều cao. - Diện tích trồng xoài chiếm$\dfrac{1}{4}$ diện tích đất nên để tính diện tích đất để trồng xoài ta lấy diện tích cả mảnh vườn chia cho \(4\) . - Tính diện tích đất để trồng cam ta lấy diện tích cả mảnh vườn trừ đi diện tích đất để trồng xoài. Lời giải chi tiết :
Chiều cao của mảnh vườn đó là: $145 - 29 = 116\;(m)$ Diện tích mảnh vườn đó là: $145 \times 116 = 16820\,\,({m^2})$ Diện tích đất để trồng xoài là: $16820:4 = 4205\,\,({m^2})$ Diện tích đất để trồng cam là: $16820 - 4205\, = 12615\,\,({m^2})$ Đáp số: \(12615\,{m^2}\). Vậy đáp án đúng điền vào ô trống là \(12615\).
|
