Đề kiểm tra giữa học kì 2 - Đề số 3Đề bài
Câu 1 :
Nguyên nhân gây ra suất điện động cảm ứng trong thanh dây dẫn chuyển động trong từ trường là:
Câu 2 :
Suất điện động tự cảm được xác định bởi biểu thức nào sau đây?
Câu 3 :
Dòng điện trong cuộn tự cảm giảm từ 16A đến 0A trong 0,01s; suất điện động tự cảm trong đó có giá trị trung bình 64V; độ tự cảm có giá trị:
Câu 4 :
Trong hình vẽ sau hình nào chỉ đúng hướng của lực Lorenxơ tác dụng lên hạt mang điện dương chuyển động trong từ trường đều:
Câu 5 :
Một electron có vận tốc 2.105m/s đi vào trong điện trường đều vuông góc với đường sức điện trường có cường độ 104V/m. Để cho electron chuyển động thẳng đều trong điện trường, ngoài điện trường còn có từ trường. Xác định chiều véctơ cảm ứng từ và độ lớn của cảm ứng từ? 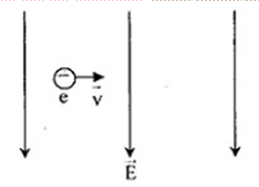
Câu 6 :
Một khung dây hình tam giác vuông có độ dài cạnh huyền là 10cm và một cạnh góc vuông là 8cm. Cả khung dây được đưa vào từ trường đều sao cho các đường sức từ vuông góc với khung dây, từ thông xuyên qua khung dây là 1,2.10-7Wb. Cảm ứng từ B có giá trị:
Câu 7 :
Hai dây dẫn thẳng, rất dài, đặt trong không khí, trùng với hai trục tọa độ vuông góc $xOy$. Dòng điện qua dây $Ox$ chạy cùng chiều với chiều dương của trục tọa độ và có cường độ $I_1= 2A$ , dòng điện qua dây $Oy$ chạy ngược chiều với chiều dương của trục tọa độ và có cường độ $I_2= 3 A$. Xác định cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm $M$ có tọa độ $x = 4 cm$ và $y = -2 cm$
Câu 8 :
Phát biểu nào sau đây là không đúng?
Câu 9 :
Phát biểu nào sau đây là không đúng? Từ trường đều là từ trường có
Câu 10 :
Độ lớn của suất điện động cảm ứng trong một mạch kín được xác định theo công thức:
Câu 11 :
Phát biểu nào sau đây là đúng? Cho một đoạn dây dẫn mang dòng điện I đặt song song với đường sức từ, chiều của dòng điện ngược chiều với chiều của đường sức từ
Câu 12 :
Hai dây dẫn thẳng song song mang dòng điện \({I_1}\) và \({I_2}\) đặt cách nhau một khoảng $r$ trong không khí. Trên mỗi đơn vị dài của mỗi dây chịu tác dụng của lực từ có độ lớn là:
Câu 13 :
Tương tác nào sau đây là tương tác từ?
Câu 14 :
Một diện tích \(S\) đặt trong từ trường đều có cảm ứng từ \(B\), góc giữa vectơ cảm ứng từ và vectơ pháp tuyến là \(\alpha \). Từ thông qua diện tích \(S\) được tính theo công thức:
Câu 15 :
Một hình vuông cạnh \(5cm\), đặt trong từ trường đều có cảm ứng từ \(B = {4.10^{ - 4}}T\). Từ thông qua hình vuông đó bằng \({10^{ - 6}}{\rm{W}}b\). Góc hợp bởi vectơ cảm ứng từ và vectơ pháp tuyến với hình vuông đó là:
Câu 16 :
Một khung dây phẳng, diện tích \(20{\rm{ }}\left( {c{m^2}} \right)\), gồm \(10\) vòng dây đặt trong từ trường đều. Vectơ cảm ứng từ làm thành với mặt phẳng khung dây một góc \({30^0}\) và có độ lớn \(B{\rm{ }} = {\rm{ }}{2.10^{ - 4}}\left( T \right)\). Người ta làm cho từ trường giảm đều đến không trong khoảng thời gian \(0,01{\rm{ }}\left( s \right)\). Suất điện động cảm ứng xuất hiện trong khung dây trong khoảng thời gian từ trường biến đổi là:
Câu 17 :
Phát biểu nào sau đây là đúng?
Câu 18 :
Lực Lorenxơ là:
Câu 19 :
Hai dòng điện thẳng dài đặt song song cùng chiều, cách nhau \(d = 12cm\) trong không khí có \({I_2} = {I_1} = I = 10A\). Xác định cảm ứng từ tổng hợp tại điểm M cách đều \({I_1}\) và \({I_2}\) một khoảng x. Hãy xác định x để độ lớn cảm ứng từ tổng hợp do hai dòng điện gây ra đạt giá trị cực đại. Tính giá trị cực đại đó
Câu 20 :
Phát biểu nào sau đây là không đúng?
Câu 21 :
Một dây dẫn có chiều dài \(10m\) đặt trong từ trường đều \(B = {5.10^{ - 2}}T\) . Cho dòng điện có cường độ \(10A\) chạy qua dây dẫn. Nếu lực từ tác dụng có độ lớn bằng \(2,5\sqrt 3 N\) thì khi đó góc giữa \(\overrightarrow B \) và chiều dòng điện là:
Câu 22 :
Cho hệ thống như hình vẽ: 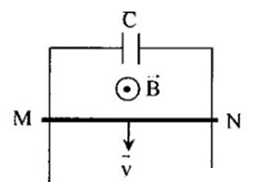 Thanh MN có chiều dài \(20cm\) chuyển động với vận tốc \(2m/s\) trong từ trường đều \(B{\rm{ }} = 0,04T\). Tụ điện có điện dung \(C = 2\mu F\). Độ lớn điện tích của tụ điện:
Câu 23 :
Ba dây dẫn thẳng dài được đặt song song trong cùng mặt phẳng thẳng đứng như hình vẽ. Dây 1 và dây 3 được giữ cố định có dòng điện chạy xuống và I1 > I3 . Xác định chiều của dòng I2 nếu dây 2 bị dịch sang trái? 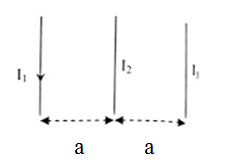
Câu 24 :
Cho một khung dây hình chữ nhật ABCD có \(AB{\rm{ }} = {\rm{ }}10{\rm{ }}cm\) ; \(BC{\rm{ }} = {\rm{ }}20{\rm{ }}cm\) , có dòng điện \(I{\rm{ }} = {\rm{ }}5{\rm{ }}A\) chạy qua đặt trong một từ trường đều có các đường sức từ song song với mặt phẵng chứa khung dây và hợp với cạnh AD một góc \(\alpha = {\rm{ }}{30^0}\) như hình vẽ. Biết \(B{\rm{ }} = {\rm{ }}0,02{\rm{ }}T\). Độ lớn lực từ do từ trường đều tác dụng lên cạnh DC của khung dây là: 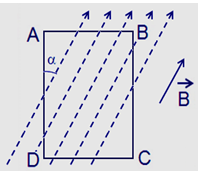
Câu 25 :
Một hạt mang điện chuyển động với vận tốc \(\overrightarrow v \) vào trong từ trường theo phương song song với đường sức từ thì:
Lời giải và đáp án
Câu 1 :
Nguyên nhân gây ra suất điện động cảm ứng trong thanh dây dẫn chuyển động trong từ trường là:
Đáp án : B Lời giải chi tiết :
Nguyên nhân gây ra suất điện động cảm ứng trong thanh dây dẫn chuyển động trong từ trường là do lực Lorenxơ tác dụng lên các electron làm các electron dịch chuyển từ đầu này sang đầu kia của thanh
Câu 2 :
Suất điện động tự cảm được xác định bởi biểu thức nào sau đây?
Đáp án : C Lời giải chi tiết :
Suất điện động tự cảm được xác định bởi biểu thức: \({e_{tc}} = - L\frac{{\Delta i}}{{\Delta t}}\)
Câu 3 :
Dòng điện trong cuộn tự cảm giảm từ 16A đến 0A trong 0,01s; suất điện động tự cảm trong đó có giá trị trung bình 64V; độ tự cảm có giá trị:
Đáp án : B Phương pháp giải :
Vận dụng biểu thức \({e_{tc}} = - L\frac{{\Delta i}}{{\Delta t}}\) Lời giải chi tiết :
Ta có: \(\left| {{e_{tc}}} \right| = L\frac{{\left| {\Delta i} \right|}}{{\Delta t}} \to L = \frac{{\left| {{e_{tc}}} \right|\Delta t}}{{\left| {\Delta i} \right|}} = \frac{{64.0,01}}{{16}} = 0,04(H)\)
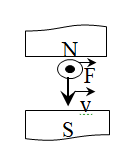
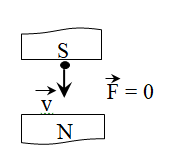
Câu 4 :
Trong hình vẽ sau hình nào chỉ đúng hướng của lực Lorenxơ tác dụng lên hạt mang điện dương chuyển động trong từ trường đều:
Đáp án : D Lời giải chi tiết :
* Quy tắc bàn tay trái: Đặt bàn tay trái sao cho cảm ứng từ \(\overrightarrow B \) xuyên vào lòng bàn tay. Chiều từ cổ tay đến các ngón tay là chiều của \(\overrightarrow v \). Chiều của \(f\) cùng chiều với ngón cái choãi ra 900 nếu q > 0 và ngược chiều với ngón cái choãi ra 900 nếu q < 0. 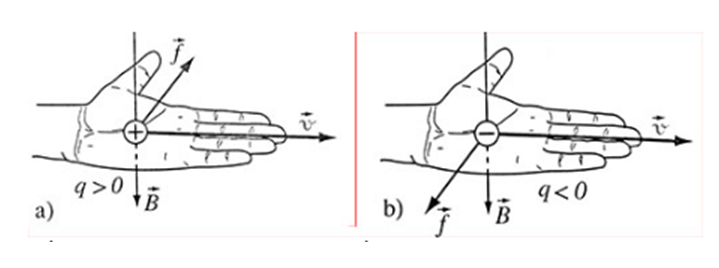 D- vận tốc // cảm ứng từ => Lực lorenxơ
Câu 5 :
Một electron có vận tốc 2.105m/s đi vào trong điện trường đều vuông góc với đường sức điện trường có cường độ 104V/m. Để cho electron chuyển động thẳng đều trong điện trường, ngoài điện trường còn có từ trường. Xác định chiều véctơ cảm ứng từ và độ lớn của cảm ứng từ? 
Đáp án : C Phương pháp giải :
+ Áp dụng các quy tắc, xác định phương chiều của lực điện, lực lorenxơ + Vận dụng điều kiện để chuyển động của vật là thẳng đều Lời giải chi tiết :
+ Trong điện trường, electron chịu tác dụng của lực điện: \(\overrightarrow {{F_d}} = q\overrightarrow E = e\overrightarrow E \) + Vì e < 0 => lực điện \(\overrightarrow {{F_d}} \) ngược chiều vưới điện trường \(\overrightarrow E \) + Để electron chuyển động thẳng đều thì hợp lực tác dụng lên electron phải bằng 0. Do đó, lực lorenxơ phải cân bằng với lực điện trường => Lực lorenxơ phải ngược chiều với lực điện + Áp dụng quy tắc bàn tay trái, ta suy ra chiều của cảm ứng từ \(\overrightarrow B \) có chiều từ ngoài vào trong mặt phẳng hình vẽ 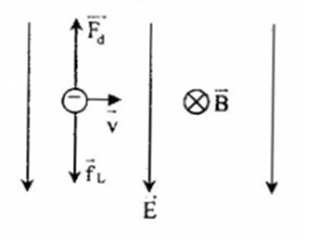 + Mặt khác: \(f = {F_d} \leftrightarrow \left| e \right|vB = \left| e \right|E \to B = \frac{E}{v} = \frac{{{{10}^4}}}{{{{2.10}^5}}} = 0,05(T)\)
Câu 6 :
Một khung dây hình tam giác vuông có độ dài cạnh huyền là 10cm và một cạnh góc vuông là 8cm. Cả khung dây được đưa vào từ trường đều sao cho các đường sức từ vuông góc với khung dây, từ thông xuyên qua khung dây là 1,2.10-7Wb. Cảm ứng từ B có giá trị:
Đáp án : B Phương pháp giải :
+ Sử dụng các công thức trong tam giác vuông + Vận dụng biểu thức tính từ thông qua diện tích S: \(\Phi = BSc{\rm{os}}\alpha \) Lời giải chi tiết :
Cạnh còn lại của tam giác có giá trị: 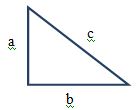 Ta có: c = 10cm, b = 8cm Theo định lý Py-ta-go: \(a = \sqrt {{c^2} - {b^2}} = \sqrt {{{10}^2} - {8^2}} = 6cm\) Diện tích của tam giác: \(S = \frac{1}{2}a.b = \frac{1}{2}0,06.0,08 = 2,{4.10^{ - 3}}({m^2})\) Từ thông qua khung dây: \(\Phi = BSc{\rm{os}}{{\rm{0}}^0} \to B = \frac{\Phi }{S} = \frac{{1,{{2.10}^{ - 7}}}}{{2,{{4.10}^{ - 3}}}} = {5.10^{ - 5}}(T)\)
Câu 7 :
Hai dây dẫn thẳng, rất dài, đặt trong không khí, trùng với hai trục tọa độ vuông góc $xOy$. Dòng điện qua dây $Ox$ chạy cùng chiều với chiều dương của trục tọa độ và có cường độ $I_1= 2A$ , dòng điện qua dây $Oy$ chạy ngược chiều với chiều dương của trục tọa độ và có cường độ $I_2= 3 A$. Xác định cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm $M$ có tọa độ $x = 4 cm$ và $y = -2 cm$
Đáp án : D Phương pháp giải :
+ Áp dụng các bước giải xác định cảm ứng từ (Xem lí thuyết phần V) + Áp dụng biểu thức xác định cảm ứng từ của dòng điện thẳng: \(B = {2.10^{ - 7}}\dfrac{I}{r}\) Lời giải chi tiết :
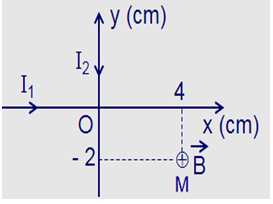 Dòng I1 gây ra tại $M$ véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) vuông góc với mặt phẵng $xOy$, hướng từ ngoài vào, có độ lớn: \({B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{|y|}} = {\rm{ }}{2.10^{ - 5}}T\) Dòng I2 gây ra tại A véc tơ cảm ứng từ \(\mathop {{B_2}}\limits^ \to \) vuông góc với mặt phẵng xOy, hướng từ trong ra, có độ lớn: \({B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{|x|}} = {\rm{ }}1,{5.10^{ - 5}}T\) Cảm ứng từ tổng hợp tại A là \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \). Vì \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) cùng phương, ngược chiều và B1 > B2 nên \(\mathop B\limits^ \to \) cùng phương, cùng chiều với\(\mathop {{B_1}}\limits^ \to \) và có độ lớn B = B1 – B2 = 0,5.10-5 T.
Câu 8 :
Phát biểu nào sau đây là không đúng?
Đáp án : B Lời giải chi tiết :
A, C, D - đúng B- sai
Câu 9 :
Phát biểu nào sau đây là không đúng? Từ trường đều là từ trường có
Đáp án : C Lời giải chi tiết :
A, B, D - đúng C- sai vì: hạt mang điện đứng yên đặt trong từ trường không chịu tác dụng lực từ
Câu 10 :
Độ lớn của suất điện động cảm ứng trong một mạch kín được xác định theo công thức:
Đáp án : A Lời giải chi tiết :
Suất điện động cảm ứng trong một mạch kín được xác định bởi biểu thức: \({e_C} = \frac{{\left| {\Delta \Phi } \right|}}{{\Delta t}}\)
Câu 11 :
Phát biểu nào sau đây là đúng? Cho một đoạn dây dẫn mang dòng điện I đặt song song với đường sức từ, chiều của dòng điện ngược chiều với chiều của đường sức từ
Đáp án : A Phương pháp giải :
Vận dụng biểu thức xác định lực từ tác dụng lên đoạn dây dẫn mang dòng điện: \(F = BIl{\rm{sin}}\alpha \) Lời giải chi tiết :
Khi đoạn dây đặt // với đường sức từ \(\alpha = 180 \to F = BIl\sin \alpha {\rm{ = 0}}\) => Lực từ luôn bằng không khi tăng hay giảm cường độ dòng điện
Câu 12 :
Hai dây dẫn thẳng song song mang dòng điện \({I_1}\) và \({I_2}\) đặt cách nhau một khoảng $r$ trong không khí. Trên mỗi đơn vị dài của mỗi dây chịu tác dụng của lực từ có độ lớn là:
Đáp án : C Phương pháp giải :
Vận dụng biểu thức tính lực tương tác giữa hai dòng điện song song: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}l\) Lời giải chi tiết :
Lực tương tác giữa hai dòng điện song song: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}l\) => Trên mỗi đơn vị chiều dài mỗi dây chịu tác dụng của lực từ có độ lớn là: \(F' = \dfrac{F}{l} = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}\)
Câu 13 :
Tương tác nào sau đây là tương tác từ?
Đáp án : D Lời giải chi tiết :
Ta có tương tác từ gồm tương tác : - Giữa nam châm với nam châm - Giữa nam châm với dòng điện - Giữa dòng điện với dòng điện => A, B, C – không phải tương tác từ D – tương tác từ
Câu 14 :
Một diện tích \(S\) đặt trong từ trường đều có cảm ứng từ \(B\), góc giữa vectơ cảm ứng từ và vectơ pháp tuyến là \(\alpha \). Từ thông qua diện tích \(S\) được tính theo công thức:
Đáp án : B Phương pháp giải :
Sử dụng biểu thức xác định từ thông qua diện tích \(S\) Lời giải chi tiết :
Một diện tích \(S\) đặt trong từ trường đều có cảm ứng từ \(B\), góc giữa vectơ cảm ứng từ và vectơ pháp tuyến là \(\alpha \) Từ thông qua diện tích \(S\) được tính theo công thức \(\Phi = BScos\alpha \)
Câu 15 :
Một hình vuông cạnh \(5cm\), đặt trong từ trường đều có cảm ứng từ \(B = {4.10^{ - 4}}T\). Từ thông qua hình vuông đó bằng \({10^{ - 6}}{\rm{W}}b\). Góc hợp bởi vectơ cảm ứng từ và vectơ pháp tuyến với hình vuông đó là:
Đáp án : A Phương pháp giải :
+ Vận dụng biểu thức tính từ thông: \(\Phi = BScos\alpha \) với \(\alpha = (\overrightarrow n ,\overrightarrow B )\) + Sử dụng biểu thức tính diện tích hình vuông: \(S = {a^2}\) Lời giải chi tiết :
Ta có từ thông qua diện tích hình chữ nhật: \(\Phi = BScos\alpha \) + Diện tích \(S\) của hình vuông: \(S = {0,05^2} = {2,5.10^{ - 3}}{m^2}\) + Từ thông qua hình vuông: \(\Phi = {10^{ - 6}}{\rm{W}}b\) \(\begin{array}{l} \to cos\alpha = \dfrac{\Phi }{{BS}} = \dfrac{{{{10}^{ - 6}}}}{{{{4.10}^{ - 4}}{{.2,5.10}^{ - 3}}}} = 1\\ \to \alpha = {0^0}\end{array}\)
Câu 16 :
Một khung dây phẳng, diện tích \(20{\rm{ }}\left( {c{m^2}} \right)\), gồm \(10\) vòng dây đặt trong từ trường đều. Vectơ cảm ứng từ làm thành với mặt phẳng khung dây một góc \({30^0}\) và có độ lớn \(B{\rm{ }} = {\rm{ }}{2.10^{ - 4}}\left( T \right)\). Người ta làm cho từ trường giảm đều đến không trong khoảng thời gian \(0,01{\rm{ }}\left( s \right)\). Suất điện động cảm ứng xuất hiện trong khung dây trong khoảng thời gian từ trường biến đổi là:
Đáp án : B Phương pháp giải :
+ Vận dụng biểu thức tính độ lớn của suất điện động cảm ứng khung dây có N vòng dây: \({e_c} = N.\left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right|\) + Vận dụng biểu thức tính từ thông: \(\Phi = BScos\alpha \) với \(\alpha = (\overrightarrow n ,\overrightarrow B )\) Lời giải chi tiết :
Ta có: + Góc \(\alpha = (\overrightarrow n ,\overrightarrow B ) = {90^0} - {30^0} = {60^0}\) => Từ thông ban đầu qua khung dây: \(\Phi = BScos\alpha = {2.10^{ - 4}}{.20.10^{ - 4}}.cos{60^0} = {2.10^{ - 7}}{\rm{W}}b\) + Suất điện động cảm ứng qua khung dây trong khoảng thời gian: \({e_c} = N\dfrac{{\left| {\Delta \Phi } \right|}}{{\Delta t}} = 10.\dfrac{{\left| {0 - {{2.10}^{ - 7}}} \right|}}{{0,01}} = {2.10^{ - 4}}V = 0,2mV\)
Câu 17 :
Phát biểu nào sau đây là đúng?
Đáp án : B Phương pháp giải :
Sử dụng quy tắc bàn tay phải xác định chiều suất điện động trong thanh Lời giải chi tiết :
Quy tắc bàn tay phải để xác định chiều của suất điện động trong thanh: Đặt bàn tay phải hứng các đường sức từ, ngón tay cái choãi ra \({90^0}\) hướng theo chiều chuyển động của đoạn dây, khi đó đoạn dây dẫn đóng vai trò như một nguồn điện, chiều từ cổ tay đến các ngón tay chỉ chiều từ cực âm sang cực dương của nguồn điện đó.
Câu 18 :
Lực Lorenxơ là:
Đáp án : A Lời giải chi tiết :
Lực Lorenxơ là lực từ tác dụng lên mọi hạt mang điện chuyển động trong từ trường
Câu 19 :
Hai dòng điện thẳng dài đặt song song cùng chiều, cách nhau \(d = 12cm\) trong không khí có \({I_2} = {I_1} = I = 10A\). Xác định cảm ứng từ tổng hợp tại điểm M cách đều \({I_1}\) và \({I_2}\) một khoảng x. Hãy xác định x để độ lớn cảm ứng từ tổng hợp do hai dòng điện gây ra đạt giá trị cực đại. Tính giá trị cực đại đó
Đáp án : A Phương pháp giải :
+ Áp dụng các bước giải xác định cảm ứng từ (Xem lí thuyết phần V) + Áp dụng biểu thức xác định cảm ứng từ của dòng điện thẳng: \(B = {2.10^{ - 7}}\dfrac{I}{r}\) + Áp dụng BĐT Côsi Lời giải chi tiết :
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng \({I_1}\) đi vào tại A, dòng \({I_2}\) đi vào tại B. Các dòng điện \({I_1}\) và \({I_2}\) gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ: 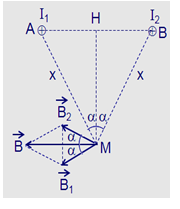 Có độ lớn: \({B_1} = {B_2} = {2.10^{ - 7}}\dfrac{I}{x}\) Từ hình ta có: \(\left\{ \begin{array}{l}AH = \dfrac{{12}}{2} = 6cm = 0,06m\\HM = \sqrt {A{M^2} - A{H^2}} = \sqrt {{x^2} - 0,{{06}^2}} \\cos\alpha = \dfrac{{HM}}{{AM}}\end{array} \right.\) Cảm ứng từ tổng hợp tại M là: \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ và có độ lớn: \(\begin{array}{l}B = 2{B_1}cos\alpha = {2.2.10^{ - 7}}\dfrac{I}{x}\dfrac{{HM}}{{AM}}\\ = {4.10^{ - 7}}.\dfrac{{10}}{x}\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{x}\\ = {4.10^{ - 6}}\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{{{x^2}}}\end{array}\) Nhận thấy, B đạt cực đại khi \(\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{{{x^2}}}\) đạt cực đại: Ta có: \(\begin{array}{l}\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{{{x^2}}} = \sqrt {\dfrac{{{x^2} - 0,{{06}^2}}}{{{x^4}}}} = \sqrt {\dfrac{1}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} \\ = \sqrt {\dfrac{1}{{0,{{06}^2}}}\dfrac{{0,{{06}^2}}}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} = \dfrac{1}{{0,06}}\sqrt {\dfrac{{0,{{06}^2}}}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} \end{array}\) Do \(d < x \to 1 - \dfrac{{0,{{06}^2}}}{{{{\rm{x}}^2}}} > 0\) Áp dụng BĐT cosi (\(\sqrt {ab} \le \dfrac{{a + b}}{2}\) ) ta có: \(\sqrt {\dfrac{{0,{{06}^2}}}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} \le \dfrac{{\dfrac{{0,{{06}^2}}}{{{x^2}}} + 1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}}}{2} = \dfrac{1}{2}\) Dấu “ = ” xảy ra khi: \(\dfrac{{0,{{06}^2}}}{{{x^2}}} = 1 - \dfrac{{0,{{06}^2}}}{{{x^2}}} \Rightarrow x = 6\sqrt 2 {.10^{ - 2}}m\) Khi đó \({B_{max}} = {4.10^{ - 6}}\dfrac{1}{{0,06}}.\dfrac{1}{2} = 3,{33.10^{ - 5}}T\)
Câu 20 :
Phát biểu nào sau đây là không đúng?
Đáp án : D Lời giải chi tiết :
Ta có: Lực từ có phương vuông góc với mặt phẳng \(\left( {\overrightarrow B ,l} \right)\) => Lực từ có phương vuông góc với đường cảm ứng từ và có phương vuông góc với dòng điện => Phương án D - sai
Câu 21 :
Một dây dẫn có chiều dài \(10m\) đặt trong từ trường đều \(B = {5.10^{ - 2}}T\) . Cho dòng điện có cường độ \(10A\) chạy qua dây dẫn. Nếu lực từ tác dụng có độ lớn bằng \(2,5\sqrt 3 N\) thì khi đó góc giữa \(\overrightarrow B \) và chiều dòng điện là:
Đáp án : D Phương pháp giải :
Vận dụng biểu thức xác định lực từ tác dụng lên đoạn dây dẫn: \(F = BIl{\rm{sin}}\alpha \) Lời giải chi tiết :
Ta có: Lực từ tác dụng lên đoạn dây dẫn mang dòng điện: \(F = BIl{\rm{sin}}\alpha \) => Góc tạo bởi \(\overrightarrow B \) và chiều dòng điện: \(\begin{array}{l}\sin \alpha = \dfrac{F}{{BIl}} = \dfrac{{2,5\sqrt 3 }}{{{{5.10}^{ - 2}}.10.10}} = \dfrac{{\sqrt 3 }}{2}\\ \Rightarrow \alpha = {60^0}\end{array}\)
Câu 22 :
Cho hệ thống như hình vẽ:  Thanh MN có chiều dài \(20cm\) chuyển động với vận tốc \(2m/s\) trong từ trường đều \(B{\rm{ }} = 0,04T\). Tụ điện có điện dung \(C = 2\mu F\). Độ lớn điện tích của tụ điện:
Đáp án : D Phương pháp giải :
+ Áp dụng biểu thức tính suất điện động trên thanh: + Áp dụng biểu thức tính điện tích trên tụ: q = CU Lời giải chi tiết :
Khi thanh MN chuyển động thì thanh MN xem như nguồn điện có suất điện động có độ lớn: \({e_C} = Blv\sin {90^0} = 0,04.0,2.2 = 0,016V\) Nguồn điện MN sẽ nạp điện cho tụ C nên điện tích của tụ C là: \(q = C{e_C} = {2.10^{ - 6}}.0,016 = 3,{2.10^{ - 8}}(C) = 32\left( {nC} \right)\)
Câu 23 :
Ba dây dẫn thẳng dài được đặt song song trong cùng mặt phẳng thẳng đứng như hình vẽ. Dây 1 và dây 3 được giữ cố định có dòng điện chạy xuống và I1 > I3 . Xác định chiều của dòng I2 nếu dây 2 bị dịch sang trái? 
Đáp án : B Phương pháp giải :
+ Vận dụng biểu thức xác định lực từ tác dụng lên mỗi đơn vị chiều dài dây: \(F = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{r}\) + Vận dụng quy tắc tổng hợp lực Lời giải chi tiết :
Ta có: \({F_{12}} = {2.10^{ - 7}}\dfrac{{{I_1}{I_2}}}{a}\) \({F_{32}} = {2.10^{ - 7}}\dfrac{{{I_3}{I_2}}}{a}\) \({I_1} > {I_3} \to {F_{12}} > {F_{23}}\) Muốn dây 2 dịch sang trái thì F12 phải hướng sang trái => F12 là lực hút => I1 và I2 cùng chiều nhau => I2 hướng xuống Chú ý
Với điều kiện I1 và I2 cùng chiều nhau Và có \({F_{12}} > {F_{32}}\) nên dù \({I_2}\) và \({I_3}\) cùng chiều hay ngược chiều thì dây thứ 2 đều dịch sang trái => Nếu chọn phương án D thì phải thêm điều kiện “và cùng chiều với I1”
Câu 24 :
Cho một khung dây hình chữ nhật ABCD có \(AB{\rm{ }} = {\rm{ }}10{\rm{ }}cm\) ; \(BC{\rm{ }} = {\rm{ }}20{\rm{ }}cm\) , có dòng điện \(I{\rm{ }} = {\rm{ }}5{\rm{ }}A\) chạy qua đặt trong một từ trường đều có các đường sức từ song song với mặt phẵng chứa khung dây và hợp với cạnh AD một góc \(\alpha = {\rm{ }}{30^0}\) như hình vẽ. Biết \(B{\rm{ }} = {\rm{ }}0,02{\rm{ }}T\). Độ lớn lực từ do từ trường đều tác dụng lên cạnh DC của khung dây là: 
Đáp án : A Phương pháp giải :
Vận dụng biểu thức tính tính lực từ: \(F = BIlsin\alpha \) Lời giải chi tiết :
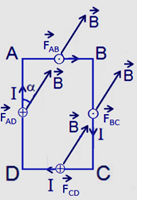 Các lực từ tác dụng lên từng cạnh của khung dây có điểm đặt tại trung điểm của mỗi cạnh, có phương vuông góc với mặt phẵng chứa khung dây và vuông góc với từng cạnh, lực tác dụng lên các cạnh DC hướng từ ngoài vào và có độ lớn: \(\begin{array}{l}{F_{DC}} = {\rm{ }}B.I.DC.sin\alpha \\ = 0,02.5.0,1.\sin {60^0}\\ = {8,66.10^{ - 3}}N\end{array}\)
Câu 25 :
Một hạt mang điện chuyển động với vận tốc \(\overrightarrow v \) vào trong từ trường theo phương song song với đường sức từ thì:
Đáp án : C Lời giải chi tiết :
Ta có: hạt mang điện chuyển động theo phương song song với đường sức từ => lực lorenxơ \(f = 0\) => Hạt không chịu tác dụng của lực lorenxơ => vận tốc và hướng chuyển động của hạt không thay đổi |




















Danh sách bình luận