Đề kiểm tra 15 phút chương 1: Điện tích - Điện trường - Đề số 01

- Các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \), lực căng dây \(\overrightarrow T \), lực tương tác tĩnh điện\(\overrightarrow F \).

- Khi quả cầu cân bằng, ta có: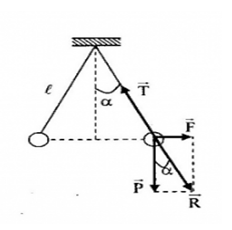

\(\overrightarrow T  + \overrightarrow P  + \overrightarrow F  = 0 \leftrightarrow \overrightarrow T  + \overrightarrow R  = 0\)

=> \(\overrightarrow R \)cùng phương, ngược chiều với \(\overrightarrow T \)

Ta có: \(\tan \alpha  = \frac{F}{P} = \frac{{\frac{r}{2}}}{{\sqrt {{l^2} - {{\left( {\frac{r}{2}} \right)}^2}} }} \to F = P\frac{{\frac{r}{2}}}{{\sqrt {{l^2} - {{\left( {\frac{r}{2}} \right)}^2}} }}\)

+ Ta có:

\(\begin{array}{l}{l^2} \gg {\left( {\frac{r}{2}} \right)^2} \to {l^2} - {\left( {\frac{r}{2}} \right)^2} \approx {l^2}\\ \to \sqrt {{l^2} - {{\left( {\frac{r}{2}} \right)}^2}}  \approx l \to F \approx \frac{{P{\rm{r}}}}{{2l}}\end{array}\)

+ Lúc đầu: \({F_1} = k\frac{{{q^2}}}{{{r^2}}} = \frac{{\Pr }}{{2l}}\)                                 (1)

+ Giả sử ta chạm tay vào quả 1, kết quả sau đó quả cầu 1 sẽ mất điện tích, lúc đó giữa hai quả cầu không còn lực tương tác nên chúng sẽ trở về vị trí dây treo thẳng đứng.

+ Khi chúng vừa chạm vào nhau thì điện tích của quả 2 sẽ truyền sang quả 1 và lúc này điện tích mỗi quả sẽ là:

\({q_1}' = {q_2}' = \frac{{{q_2}}}{2} = \frac{q}{2} \to {F_2} = k\frac{{{q^2}}}{{4.r{'^2}}}{\rm{ = }}\frac{{P{\rm{r}}'}}{{2l}}{\rm{                (2)}}\)

Từ (1) và (2) ta có:

\(\frac{{{F_1}}}{{{F_2}}} = \frac{{k\frac{{{q^2}}}{{{r^2}}}}}{{k\frac{{{q^2}}}{{4.r{'^2}}}}} = \frac{{\frac{{\Pr }}{{2l}}}}{{\frac{{P{\rm{r}}'}}{{2l}}}} \leftrightarrow \frac{{4r{'^2}}}{{{r^2}}} = \frac{r}{{r'}} \leftrightarrow 4{\rm{r}}{'^3} = {r^3} \to r' = \frac{r}{{\sqrt(3){4}}} = \frac{{6,35}}{{\sqrt(3){4}}} \approx 4cm\)