Đề khảo sát chất lượng đầu năm lớp 11 môn Lí - Đề số 1Đề bài
Câu 1 :
Chuyển động cơ học là sự thay đổi:
Câu 2 :
Trong trường hợp nào dưới đây số chỉ thời điểm mà ta xét trùng với số đo khoảng thời gian trôi?
Câu 3 :
Đồ thị vận tốc - thời gian của chuyển động thẳng đều là:
Câu 4 :
Một chất điểm chuyển động thẳng đều có đồ thị tọa độ thời gian như hình vẽ. Phương trình chuyển động của vật là: 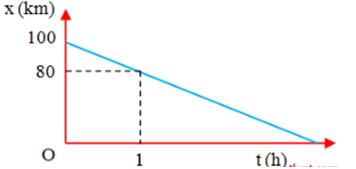
Câu 5 :
Một thanh cứng, mảnh $AB$ có chiều dài \(l = 2m\) dựng đứng sát bức tường thẳng đứng như hình. Ở đầu $A$ của thanh có một con kiến. Khi đầu $A$ của thanh bắt đầu chuyển động trên sàn ngang về bên phải theo phương vuông góc với bức tường thì con kiến cũng bắt đầu bò dọc theo thanh. Đầu $A$ chuyển động thẳng đều với vận tốc \({v_1} = 0,5cm/s\) so với sàn kể từ vị trí tiếp xúc với bức tường. Con kiến bò thẳng đều với vận tốc \({v_2} = 0,2cm/s\) so với thanh kể từ đầu $A$. Độ cao cực đại của con kiến đối với sàn ngang là bao nhiêu? Biết rằng đầu B của thanh luôn tiếp xúc với tường. 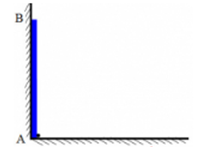
Câu 6 :
Một ôtô đang chuyển động với vận tốc $54km/h$ thì hãm phanh, chuyển động chậm dần đều và dừng lại sau $10s$. Chọn chiều dương là chiều chuyển động của ôtô .Vận tốc của ôtô sau khi hãm phanh được $6s$ là:
Câu 7 :
Một chiếc xe hơi giảm tốc chậm dần đều từ $54km/h$ còn $36km/h$ trên quãng đường thẳng dài $125m$. Vậy gia tốc của xe trên đoạn đường này là:
Câu 8 :
Một vật rơi tự do không vận tốc đầu từ một điểm A vào lúc t = 0. Phương trình của vật khi chọn gốc toạ độ là vị trí O ở dưới A một khoảng 196m, chiều dương hướng xuống là : (g = 9,8m/s2)
Câu 9 :
Khi loại bỏ được ảnh hưởng của không khí thì các vật sẽ rơi:
Câu 10 :
Lực là:
Câu 11 :
Chọn phát biểu đúng?
Câu 12 :
Một vật có trọng lượng P đứng cân bằng nhờ 2 dây OA làm với trần một góc 600 và OB nằm ngang. Độ lớn lực căng T1 của dây OA bằng: 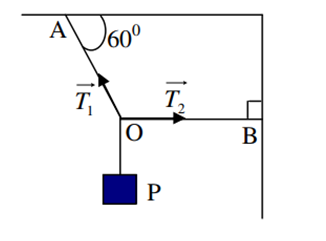
Câu 13 :
Một ôtô có khối lưọng $500kg$ đang chuyển động thẳng đều thì hãm phanh chuyển động chậm dần đều trong $2s$ cuối cùng đi được $1,8 m$. Hỏi lực hãm phanh tác dụng lên ôtô có độ lớn là bao nhiêu?
Câu 14 :
Lực F truyền cho vật khối lượng m1 thì vật có gia tốc \({a_1} = 2m/{s^2}\) , truyền cho vật khối lượng m2 thì vật có \({a_2} = 3m/{s^2}\). Hỏi lực F sẽ truyền cho vật có khối lượng m3 = m1 + m2 thì vật có gia tốc là bao nhiêu?
Câu 15 :
Một vật chuyển động tròn đều với quỹ đạo có bán kính \(r\), tốc độ góc \(\omega \). Biểu thức liên hệ giữa gia tốc hướng tâm a của vật với tần số góc \(\omega \) và bán kính \(r\) là:
Câu 16 :
Một vật chuyển động tròn đều với tốc độ dài là \(5{\rm{ }}m/s\) và có tốc độ góc \(10{\rm{ }}rad/s\). Gia tốc hướng tâm của vật đó có độ lớn là:
Câu 17 :
Nhận xét nào sau đây của hành khách ngồi trên đoàn tàu đang chạy là không đúng?
Câu 18 :
Biểu thức nào sau đây là biểu thức đúng của công thức cộng vận tốc:
Câu 19 :
Chọn phương án đúng.
Câu 20 :
Trong tọa độ \(\left( {p,V} \right)\)đường đẳng nhiệt là:
Câu 21 :
Một lượng khí xác định ở áp suất \(3{\rm{a}}tm\) có thể tích là \(10\) lít. Thể tích của khối khí khi nén đẳng nhiệt đến áp suất \(6{\rm{a}}tm\)?
Câu 22 :
Khi nói về lực đàn hồi của lò xo. Phát biểu nào sau đây là sai?
Câu 23 :
Nội năng của vật là:
Câu 24 :
Trường hợp làm biến đổi nội năng không do thực hiện công là?
Câu 25 :
Một vệ tinh nhân tạo có khối lượng \(100{\rm{ }}kg\), được phóng lên quỹ đạo quanh Trái Đất ở độ cao mà tại đó nó có trọng lượng 920 N. Chu kì của vệ tinh là \(5,{3.10^3}{\rm{ s}}\). Biết bán kính Trái Đất là \(R = 6400{\rm{ km}}\). Khoảng cách từ bề mặt Trái Đất đến vệ tinh.
Câu 26 :
Một vật đang chuyển động có thể không có:
Câu 27 :
Một người và xe máy có khối lượng tổng cộng là \(300 kg\) đang đi với vận tốc \(36 km/h\) thì nhìn thấy một cái hố cách \(12 m\). Để không rơi xuống hố thì người đó phải dùng một lực hãm có độ lớn tối thiểu là:
Câu 28 :
Từ điểm A của một mặt bàn phẳng nghiêng, người ta thả một vật có khối lượng \(m = 0,2kg\) trượt không ma sát với vận tốc ban đầu bằng 0 rơi xuống đất. Cho \(AB = 50cm\), \(BC = 100cm\), \(AD = 130cm\), \(g = 10m/{s^2}\). Bỏ qua lực cản không khí. Vận tốc của vật tại điểm B có giá trị là? 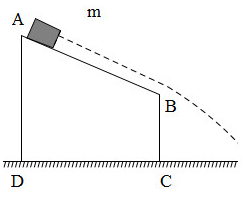
Câu 29 :
Điều kiện cân bằng của một vật có mặt chân đế là giá của trọng lực
Câu 30 :
Một thanh sắt AB đồng chất, tiết diện đều, dài 10m và nặng 40N đặt trên mặt đất phẳng ngang. Người ta tác dụng một lực F hướng thẳng đứng lên phía trên để nâng đầu B của thanh sắt lên và giữ nó ở độ cao h = 6m so với mặt đất. Độ lớn của lực F bằng bao nhiêu ?
Lời giải và đáp án
Câu 1 :
Chuyển động cơ học là sự thay đổi:
Đáp án : D Lời giải chi tiết :
Chuyển động cơ là sự dời chỗ của vật theo thời gian
Câu 2 :
Trong trường hợp nào dưới đây số chỉ thời điểm mà ta xét trùng với số đo khoảng thời gian trôi?
Đáp án : C Lời giải chi tiết :
Trong các trường hợp trên, thời điểm mà ta xét trùng với số đo khoảng thời gian trôi là: Một đoàn tàu xuất phát từ Vinh lúc $0$ giờ, đến $8$ giờ $05$ phút thì đoàn tàu đến Huế.
Câu 3 :
Đồ thị vận tốc - thời gian của chuyển động thẳng đều là:
Đáp án : B Lời giải chi tiết :
Trong chuyển động thẳng đều, vận tốc không thay đổi \(v = {v_0}\) Suy ra: Đồ thị biểu diễn vận tốc theo thời gian là một đường thẳng song song với trục thời gian.
Câu 4 :
Một chất điểm chuyển động thẳng đều có đồ thị tọa độ thời gian như hình vẽ. Phương trình chuyển động của vật là: 
Đáp án : A Lời giải chi tiết :
Phương trình chuyển động: \(x = {x_0} + vt\) Từ đồ thị x-t, ta có: + Tại thời điểm \({t_0} = 0\) : \({x_0} = 100km\) + Tại \(t = 1h\): \(x = 80km = {x_0} + v.1 \to v = \frac{{80 - 100}}{1} = - 20(km/h)\) => phương trình chuyển động của vật: \(x = 100 - 20t{\rm{ }}(km)\)
Câu 5 :
Một thanh cứng, mảnh $AB$ có chiều dài \(l = 2m\) dựng đứng sát bức tường thẳng đứng như hình. Ở đầu $A$ của thanh có một con kiến. Khi đầu $A$ của thanh bắt đầu chuyển động trên sàn ngang về bên phải theo phương vuông góc với bức tường thì con kiến cũng bắt đầu bò dọc theo thanh. Đầu $A$ chuyển động thẳng đều với vận tốc \({v_1} = 0,5cm/s\) so với sàn kể từ vị trí tiếp xúc với bức tường. Con kiến bò thẳng đều với vận tốc \({v_2} = 0,2cm/s\) so với thanh kể từ đầu $A$. Độ cao cực đại của con kiến đối với sàn ngang là bao nhiêu? Biết rằng đầu B của thanh luôn tiếp xúc với tường. 
Đáp án : A Lời giải chi tiết :
Ta có: 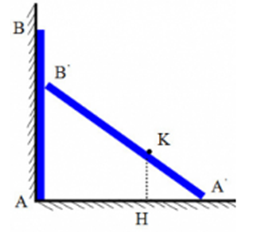 + Khi đầu $A$ của thanh di chuyển từ $A$ đến $A’$ thì con kiến di chuyển từ $A’$ đến $K$ trong cùng một khoảng thời gian. + Khi đó: \(\dfrac{{{s_{{\rm{AA'}}}}}}{{{v_1}}} = \dfrac{{{s_{A'K}}}}{{{v_2}}} \to \dfrac{{{s_{{\rm{AA'}}}}}}{{{s_{A'K}}}} = \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{0,5}}{{0,2}} = 2,5\) => Nếu quãng đường con kiến di chuyển là \({s_{A'K}} = x \to {s_{AA'}} = 2,5x\) Từ hình, ta có: \({\left( {AB'} \right)^2} = {2^2} - {\left( {2,5{\rm{x}}} \right)^2} = 4 - 6,25{{\rm{x}}^2}\) Mặt khác, ta có: \(\begin{array}{l}\Delta A'KH \sim \Delta A'B'A\\ \to \dfrac{{HK}}{{AB'}} = \dfrac{{A'K}}{{A'B'}}\\ \to H{K^2} = {\left( {AB'} \right)^2}{\left( {\dfrac{{A'K}}{{A'B'}}} \right)^2} = (4 - 6,25{{\rm{x}}^2})\dfrac{{x{}^2}}{4} = - 1,5625{{\rm{x}}^4} + {x^2}\end{array}\) Để HK có giá trị cực đại thì: \({x^2} = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{1}{{2.1,5625}} = 0,32\) Khi đó: \(H{K_{{\rm{max}}}} = \sqrt { - 1,5625.0,{{32}^2} + 0,32} = 0,4(m)\)
Câu 6 :
Một ôtô đang chuyển động với vận tốc $54km/h$ thì hãm phanh, chuyển động chậm dần đều và dừng lại sau $10s$. Chọn chiều dương là chiều chuyển động của ôtô .Vận tốc của ôtô sau khi hãm phanh được $6s$ là:
Đáp án : B Phương pháp giải :
+ Vận dụng biểu thức xác định gia tốc của chuyển động: \(a = \frac{{\Delta v}}{{\Delta t}}\) + Viết phương trình vận tốc + Thay t vào phương trình vận tốc Lời giải chi tiết :
Đổi \(54km/h = 15m/s\) Gia tốc của xe: \(a = \frac{{0 - 15}}{{10}} = - 1,5m/{s^2}\) Phương trình vận tốc của vật: \(v = 15 - 1,5t\) Vận tốc của xe sau khi hãm phanh 6 s là: \(v = 15 - 1,5.6 = 6m/s\)
Câu 7 :
Một chiếc xe hơi giảm tốc chậm dần đều từ $54km/h$ còn $36km/h$ trên quãng đường thẳng dài $125m$. Vậy gia tốc của xe trên đoạn đường này là:
Đáp án : C Phương pháp giải :
Vận dụng biểu thức độc lập: \({v^2} - v_0^2 = 2{\rm{as}}\) Lời giải chi tiết :
Đổi \(54km/h = 15m/s,\,36km/h = 10m/s\) Ta có: \({v^2} - v_0^2 = 2{\rm{as}} \to {\rm{a = }}\frac{{{v^2} - v_0^2}}{{2{\rm{s}}}} = \frac{{{{10}^2} - {{15}^2}}}{{2.125}} = - 0,5m/{s^2}\)
Câu 8 :
Một vật rơi tự do không vận tốc đầu từ một điểm A vào lúc t = 0. Phương trình của vật khi chọn gốc toạ độ là vị trí O ở dưới A một khoảng 196m, chiều dương hướng xuống là : (g = 9,8m/s2)
Đáp án : C Phương pháp giải :
Sử dụng phương trình chuyển động của vật rơi tự do: \(y = {y_0} + {v_0}t + \frac{1}{2}g{t^2}\) + Xác định vận tốc ban đầu \({v_0}\) + Xác định vị trí ban đầu của vật so với gốc tọa độ Lời giải chi tiết :
Ta có: + Vật rơi không vận tốc đầu: \( \to {v_0} = 0\) Gốc tọa độ tại O ở phía dưới A một đoạn 196m, chiều dương hướng xuống + Tọa độ ban đầu của vật: \({y_0} = - 196m\) => Phương trình chuyển động của vật: \(y = - 196 + \frac{1}{2}.9,8{t^2} = 4,9{t^2} - 196\left( m \right)\)
Câu 9 :
Khi loại bỏ được ảnh hưởng của không khí thì các vật sẽ rơi:
Đáp án : C Lời giải chi tiết :
Khi loại bỏ được ảnh hưởng của không khí thì các vật sẽ rơi tự do hay nói cách khác là chuyển động thẳng nhanh dần đều
Câu 10 :
Lực là:
Đáp án : C Lời giải chi tiết :
Lực là đại lượng véc tơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng.
Câu 11 :
Chọn phát biểu đúng?
Đáp án : D Lời giải chi tiết :
Lực là đại lượng véc tơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng.
Câu 12 :
Một vật có trọng lượng P đứng cân bằng nhờ 2 dây OA làm với trần một góc 600 và OB nằm ngang. Độ lớn lực căng T1 của dây OA bằng: 
Đáp án : B Phương pháp giải :
+ Vận dụng phương pháp tổng hợp và phân tích lực + Vận dụng điều kiện cân bằng của vật + Vận dụng biểu thức xác định hợp lực của hai lực thành phần Lời giải chi tiết :
+ Phân tích lực \({\overrightarrow T _1}\) thành hai thành phần theo phương Ox và Oy, ta có: 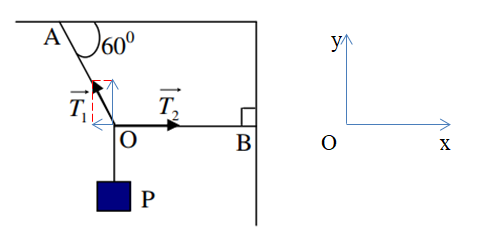 Vật cân bằng => Tổng tất cả các lực tác dụng lên vật bằng 0 Từ hình ta có: Theo phương Oy: \({T_1}\sin {60^0} = P \to {T_1} = \frac{P}{{\sin {{60}^0}}} = \frac{{2P}}{{\sqrt 3 }}\)
Câu 13 :
Một ôtô có khối lưọng $500kg$ đang chuyển động thẳng đều thì hãm phanh chuyển động chậm dần đều trong $2s$ cuối cùng đi được $1,8 m$. Hỏi lực hãm phanh tác dụng lên ôtô có độ lớn là bao nhiêu?
Đáp án : C Phương pháp giải :
+ Vận dụng biểu thức độc lập: \({v^2} - v_0^2 = 2{\rm{as}}\) + Áp dụng biểu thức tính gia tốc: \(a = \dfrac{{\Delta v}}{{\Delta t}}\) + Áp dụng định luật II Niutơn: \(\overrightarrow F = m\overrightarrow a \) Lời giải chi tiết :
+ Ta có: \({v^2} - v_0^2 = 2{\rm{as}} \to - v_0^2 = 2{\rm{as}} = 3,6{\rm{a }}(1)\) Mặt khác: \(a = \dfrac{{v - {v_0}}}{{\Delta t}} \to - {v_0} = at = 2a{\rm{ (2)}}\) Từ (1) và (2) ta suy ra: \(a = - 0,9{\rm{ }}m/{s^2}\) + Lực hãm phanh tác dụng lên ôtô: \(F = m.a{\rm{ }} = - 450N\) Chú ý
Đề bài yêu cầu tìm "lực hãm phanh tác dụng lên ôtô có độ lớn là bao nhiêu?" Các bạn chú ý đọc kĩ đầu bài, "độ lớn" là ta lấy \(\left| F \right|\) nhé
Câu 14 :
Lực F truyền cho vật khối lượng m1 thì vật có gia tốc \({a_1} = 2m/{s^2}\) , truyền cho vật khối lượng m2 thì vật có \({a_2} = 3m/{s^2}\). Hỏi lực F sẽ truyền cho vật có khối lượng m3 = m1 + m2 thì vật có gia tốc là bao nhiêu?
Đáp án : C Phương pháp giải :
Áp dụng định luật II Niutơn: \(\overrightarrow F = m\overrightarrow a \) Lời giải chi tiết :
Theo định luật II Niutơn, ta có: \(\begin{array}{l}{m_1} = \frac{F}{{{a_1}}};{m_2} = \frac{F}{{{a_2}}}\\ \to {a_3} = \frac{F}{{{m_3}}} = \frac{F}{{{m_1} + {m_2}}} = \frac{F}{{\frac{F}{{{a_1}}} + \frac{F}{{{a_2}}}}}\\ = \frac{{{a_1}{a_2}}}{{{a_1} + {a_2}}} = \frac{{2.3}}{{2 + 3}} = 1,2m/{s^2}\end{array}\)
Câu 15 :
Một vật chuyển động tròn đều với quỹ đạo có bán kính \(r\), tốc độ góc \(\omega \). Biểu thức liên hệ giữa gia tốc hướng tâm a của vật với tần số góc \(\omega \) và bán kính \(r\) là:
Đáp án : C Phương pháp giải :
+ Vận dụng biểu thức tính gia tốc hướng tâm: \({a_{ht}} = \frac{{{v^2}}}{r}\) + Vận dụng biểu thức tính vận tốc dài: \(v = \omega r\) Lời giải chi tiết :
Ta có: + Gia tốc hướng tâm: \({a_{ht}} = \frac{{{v^2}}}{r}\) + Mặt khác, vận tốc dài: \(v = \omega r\) Ta suy ra: \({a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r\)
Câu 16 :
Một vật chuyển động tròn đều với tốc độ dài là \(5{\rm{ }}m/s\) và có tốc độ góc \(10{\rm{ }}rad/s\). Gia tốc hướng tâm của vật đó có độ lớn là:
Đáp án : A Phương pháp giải :
+ Vận dụng biểu thức : \(v = \omega r\) + Vận dụng biểu thức tính gia tốc hướng tâm: \({a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r\) Lời giải chi tiết :
Ta có: + Vận tốc dài và vận tốc góc liên hệ với nhau theo biểu thức: \(v = \omega r\) (1) + Gia tốc hướng tâm của vật: \({a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r\) (2) Từ (1) và (2), ta suy ra: \({a_{ht}} = v\omega = 5.10 = 50m/{s^2}\)
Câu 17 :
Nhận xét nào sau đây của hành khách ngồi trên đoàn tàu đang chạy là không đúng?
Đáp án : B Lời giải chi tiết :
A, C, D - đúng B - sai vì: Khi hành khách ngồi trên đoàn tàu đang chạy sẽ thấy đầu tàu đứng yên so với toa tàu
Câu 18 :
Biểu thức nào sau đây là biểu thức đúng của công thức cộng vận tốc:
Đáp án : D Lời giải chi tiết :
Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \) Trong đó: + Số 1: gắn với vật cần tính vận tốc + Số 2: gắn với hệ quy chiếu là các vật chuyển động + Số 3: gắn với hệ quy chiếu là các vật đứng yên + \({v_{12}}\): vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối + \({v_{23}}\): vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo + \({v_{13}}\): vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tuyệt đối.
Câu 19 :
Chọn phương án đúng.
Đáp án : A Lời giải chi tiết :
A- đúng B, C, D - sai vì: + Áp suất không đổi: Quá trình đẳng áp + Thể tích không đổi: Quá trình đẳng tích + Nhiệt độ không đổi: Quá trình đẳng nhiệt
Câu 20 :
Trong tọa độ \(\left( {p,V} \right)\)đường đẳng nhiệt là:
Đáp án : B Lời giải chi tiết :
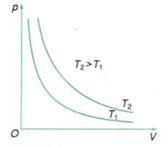 Trong hệ tọa độ (p,V) đường đẳng nhiệt là đường hypebol
Câu 21 :
Một lượng khí xác định ở áp suất \(3{\rm{a}}tm\) có thể tích là \(10\) lít. Thể tích của khối khí khi nén đẳng nhiệt đến áp suất \(6{\rm{a}}tm\)?
Đáp án : D Phương pháp giải :
Vận dụng định luật Bôilơ - Mariốt: \(pV = h/{\rm{s}}\) Lời giải chi tiết :
Trạng thái 1:\({p_1} = 3{\rm{a}}tm,{V_1} = 10l\) Trạng thái 2: \({p_2} = 6{\rm{a}}tm\) Áp dụng định luật Bôilơ - Mariốt, ta có: \({p_1}{V_1} = {p_2}{V_2} \to {V_2} = \frac{{{p_1}{V_1}}}{{{p_2}}} = \frac{{3.10}}{6} = 5l\)
Câu 22 :
Khi nói về lực đàn hồi của lò xo. Phát biểu nào sau đây là sai?
Đáp án : D Lời giải chi tiết :
A, B, C - đúng D - sai vì mỗi vật có một giới hạn đàn hồi nhất định, khi lực tác dụng vượt quá giới hạn đàn hồi thì vật đó không lấy lại được hình dạng ban đầu khi thôi tác dụng
Câu 23 :
Nội năng của vật là:
Đáp án : A Lời giải chi tiết :
Nội năng của vật là tổng động năng và thế năng của các phân tử cấu tạo nên vật.
Câu 24 :
Trường hợp làm biến đổi nội năng không do thực hiện công là?
Đáp án : A Phương pháp giải :
Vận dụng các cách thực hiện công Lời giải chi tiết :
Đung nóng nước bằng bếp là thay đổi nội năng bằng cách truyền nhiệt chứ không phải thực hiện công
Câu 25 :
Một vệ tinh nhân tạo có khối lượng \(100{\rm{ }}kg\), được phóng lên quỹ đạo quanh Trái Đất ở độ cao mà tại đó nó có trọng lượng 920 N. Chu kì của vệ tinh là \(5,{3.10^3}{\rm{ s}}\). Biết bán kính Trái Đất là \(R = 6400{\rm{ km}}\). Khoảng cách từ bề mặt Trái Đất đến vệ tinh.
Đáp án : C Phương pháp giải :
Vận dụng biểu thức tính lực hướng tâm: \({F_{ht}} = m\frac{{{v^2}}}{r}\) Lời giải chi tiết :
- Theo Niutơn thì trọng lực mà Trái Đất tác dụng lên vệ tinh chính là lực hấp dẫn giữa Trái Đất và vệ tinh. \(P = {F_{hd}} = 920{\rm{ N}}\) - Mà: \({F_{hd}} = {F_{ht}} = 920{\rm{ N}}\) \({F_{ht}} = m\frac{{{v^2}}}{r} = \frac{{m\frac{{4{\pi ^2}}}{{{T^2}}}{r^2}}}{r} = \frac{{m4{\pi ^2}r}}{{{T^2}}} \Rightarrow r = \frac{{{F_{ht}}{T^2}}}{{m4{\pi ^2}}} = \frac{{920.{{(5,{{3.10}^3})}^2}}}{{100.4{\pi ^2}}} = 6546057,712{\rm{ m}} = 6546,058{\rm{ km}}\) - Mà: \(r = R + h \Rightarrow h = r - R = 6546,058 - 6400 = 146,058{\rm{ km}}\)
Câu 26 :
Một vật đang chuyển động có thể không có:
Đáp án : C Phương pháp giải :
Vận dụng định nghĩa về động năng, động lượng, thế năng và cơ năng của vật Lời giải chi tiết :
Các đại lượng động lượng, động năng và cơ năng đều phụ thuộc vào vận tốc nên khi chuyển động, vật đều có động lượng, động năng và cơ năng nhưng vật có thể không có thế năng do cách ta chọn gốc thế năng.
Câu 27 :
Một người và xe máy có khối lượng tổng cộng là \(300 kg\) đang đi với vận tốc \(36 km/h\) thì nhìn thấy một cái hố cách \(12 m\). Để không rơi xuống hố thì người đó phải dùng một lực hãm có độ lớn tối thiểu là:
Đáp án : D Phương pháp giải :
+ Vận dụng định lý biến thiên động năng: \({{\text{W}}_{{d_2}}} - {{\text{W}}_{{d_1}}} = A\) Lời giải chi tiết :
Từ định lí biến thiên động năng ta có: \(A = {W_{d2}} - {W_{d1}} \Leftrightarrow {F_h}.s = 0 - \dfrac{1}{2}m{v^2} \Rightarrow F{}_h = - \dfrac{{m{v^2}}}{{2s}}\) \( \Rightarrow {F_h} = - \dfrac{{{{300.10}^2}}}{{2.12}} = - 1250N\) Độ lớn của lực hãm là: \( \Rightarrow {F_h} = 1250N\) dấu ‘-‘ có nghĩa là lực cản trở chuyển động.
Câu 28 :
Từ điểm A của một mặt bàn phẳng nghiêng, người ta thả một vật có khối lượng \(m = 0,2kg\) trượt không ma sát với vận tốc ban đầu bằng 0 rơi xuống đất. Cho \(AB = 50cm\), \(BC = 100cm\), \(AD = 130cm\), \(g = 10m/{s^2}\). Bỏ qua lực cản không khí. Vận tốc của vật tại điểm B có giá trị là? 
Đáp án : A Phương pháp giải :
+ Sử dụng biểu thức tính thế năng: ${{\rm{W}}_t} = mgh$ + Sử dụng biểu thức tính động năng: ${{\rm{W}}_d} = \dfrac{1}{2}m{v^2}$ + Áp dụng định luật bảo toàn cơ năng Lời giải chi tiết :
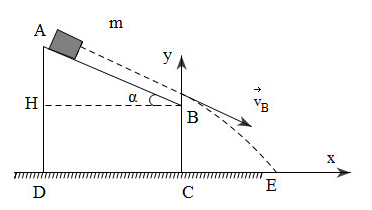 Chọn mốc thế năng tại mặt đất Vì bỏ qua ma sát nên cơ năng của vật được bảo toàn Ta có: + Cơ năng của vật tại A: ${{\rm{W}}_A} = mgAD$ (động năng của vật bằng 0 vì \({v_0} = 0\)) + Cơ năng của vật tại B: ${{\rm{W}}_B} = \dfrac{1}{2}mv_B^2 + mgBC$ Áp dụng định luật bảo toàn cơ năng, ta có cơ năng của vật tại A bằng cơ năng của vật tại B $\begin{array}{l}{{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mg.AD = \dfrac{1}{2}mv_B^2 + mg.BC\\ \leftrightarrow g.AD = \dfrac{1}{2}v_B^2 + g.BC\\ \leftrightarrow 10.1,3 = \dfrac{1}{2}v_B^2 + 10.1\\ \to {v_B} = \sqrt 6 \approx 2,45m/s\end{array}$
Câu 29 :
Điều kiện cân bằng của một vật có mặt chân đế là giá của trọng lực
Đáp án : A Phương pháp giải :
Sử dụng điều kiện cân bằng của một vật có mặt chân đế là giá của trọng lực phải xuyên qua mặt chân đế. Lời giải chi tiết :
A- đúng vì điều kiện cân bằng của một vật có mặt chân đế là giá của trọng lực phải xuyên qua mặt chân đế.
Câu 30 :
Một thanh sắt AB đồng chất, tiết diện đều, dài 10m và nặng 40N đặt trên mặt đất phẳng ngang. Người ta tác dụng một lực F hướng thẳng đứng lên phía trên để nâng đầu B của thanh sắt lên và giữ nó ở độ cao h = 6m so với mặt đất. Độ lớn của lực F bằng bao nhiêu ?
Đáp án : B Phương pháp giải :
Sử dụng điều kiện cân bằng của vật rắn có trục quay cố định (qui tắc momen lực) Lời giải chi tiết :
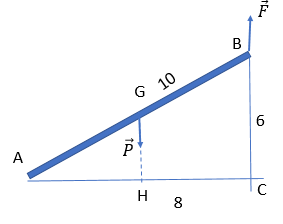 Áp dụng qui tắc momen ta có: \({M_{\overrightarrow P }} = {M_{\overrightarrow F }}\) \(\begin{array}{l} \to P.AH = F.AC\\ \to F = \dfrac{{P.AH}}{{AC}}\end{array}\)(1) Lại có: \(AC = \sqrt {A{B^2} - B{C^2}} = \sqrt {{{10}^2} - {6^2}} = 8(m)\) \(AH = AG.cosGAH = \dfrac{{AB}}{2}.cosBAC = 5.\dfrac{{AC}}{{AB}} = 5.\dfrac{8}{{10}} = 4(m)\) Thay vào (1) \( \to F = \dfrac{{40.4}}{8} = 20(N)\) |




















Danh sách bình luận