Đề kiểm tra giữa học kì 1 - Đề số 02Đề bài
Câu 1 :
Biểu thức xác định định luật Ôm cho đoạn mạch chỉ có điện trở?
Câu 2 :
Phát biểu nào sau đây là không đúng?
Câu 3 :
Một điện tích điểm q = 10-7 C đặt tại điểm M trong điện trường của một điện tích điểm Q, chịu tác dụng của một lực F = 3.10-3 N. Cường độ điện trường do điện tích điểm Q gây ra tại M có độ lớn là bao nhiêu?
Câu 4 :
Việc ghép nối tiếp các nguồn điện để
Câu 5 :
Theo nội dung của thuyết electron, phát biểu nào sau đây là sai?
Câu 6 :
Cho mạch điện như hình vẽ: E1 = 12V, r1 =1$\Omega $, E2 = 6V, r2 = 2$\Omega $, E3 = 9V, r3 = 3$\Omega $, R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = 3$\Omega $. Hiệu điện thế UAB có giá trị là: 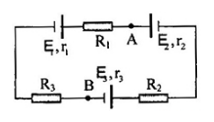
Câu 7 :
Cho mạch điện như hình vẽ: Trong đó: R1 = R2 = 4$\Omega $, R3 = 6$\Omega $, R4 = 3$\Omega $, R5 = 10$\Omega $ Tính điện trở tương đương của đoạn mạch AB? 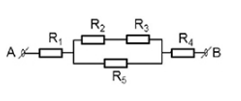
Câu 8 :
Điện tích điểm là:
Câu 9 :
OA, OB là hai đoạn dây dẫn thẳng, ACB và OBD là hai dây dẫn hình nửa đường tròn đường kính AB và OB. Các đoạn dây dẫn này đồng tính và cùng tiết diện. Biết điện trở của OA và OB bằng nhau và bằng R. Tính điện trở giữa A và B (RAB ) 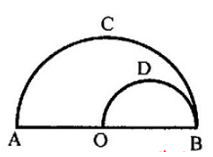
Câu 10 :
Hai điện tích dương q1, q2 có cùng một độ lớn được đặt tại hai điểm A và B, đặt một điện tích q0 vào trung điểm của AB thì ta thấy hệ ba điện tích này nằm cân bằng trong chân không. Bỏ qua trọng lượng của ba điện tích. Chọn kết luận đúng?
Câu 11 :
Câu phát biểu nào sau đây chưa đúng?
Câu 12 :
Tụ xoay có điện dung thay đổi từ \({C_1} = 30pF\) đến \({C_2} = 120pF\) khi góc xoay biến thiên từ 00 đến 900. Biết điện dung của tụ xoay là hàm bậc nhất của góc xoay . Biểu thức nào sau đây là đúng?
Câu 13 :
Một quả cầu khối lượng \(m = 4g\) treo bằng một sợi chỉ mảnh. Điện tích của quả cầu là \({q_1} = {2.10^{ - 8}}C\). Phía dưới quả cầu dọc theo phương của sợi chỉ có một điện tích \({q_2}\). Khoảng cách giữa hai điện tích là \(r = 5cm\) và lực căng dây là \(T = {5.10^{ - 2}}N\). Xác định điện tích \({q_2}\) và lực tác dụng giữa chúng, lấy \(g = 10m/{s^2}\)
Câu 14 :
Cho hai điện tích điểm đặt trong chân không. Khi khoảng cách giữa hai điện tích là \(r\) thì lực tương tác điện giữa chúng có độ lớn là \(F\). Khi khoảng cách giữa hai điện tích là \(3r\) thì lực tương tác điện giữa chúng có độ lớn là:
Câu 15 :
Để xác định điện trở trong r của một nguồn điện, một học sinh mắc mạch điện như hình (H1). Đóng khóa K và điều chỉnh con chạy C, kết quả đo được mô tả bởi đồ thị biểu diễn sự phụ thuộc của số chỉ U của vôn kế V vào số chỉ I của ampe kế A như hình (H2). Điện trở của vôn kế rất lớn. Biết \({R_0} = 2{\rm{0,3 \Omega }}\). Giá trị của r được xác định bởi thí nghiệm này là 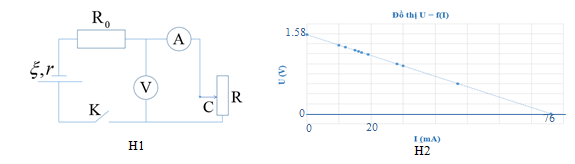
Câu 16 :
Hai quả cầu nhỏ có điện tích \(2\mu C\) và \(6\mu C\), tương tác với nhau một lực \(0,1N\) trong chân không. Khoảng cách giữa chúng là:
Câu 17 :
Cường độ điện trường tại một điểm đặc trưng cho:
Câu 18 :
Công thức xác định công của lực điện trường tác dụng lên một điện tích là \(A{\rm{ }} = {\rm{ }}qEd\) , trong đó E là:
Câu 19 :
Hai bản kim loại phẳng song song mang điện tích trái dấu được đặt cách nhau \(2cm\). Cường độ điện trường giữa hai bản bằng \(3000V/m\). Sát bề mặt mang điện dương, người ta đặt một hạt mang điện dương \(q = 1,{5.10^{ - 2}}C\), có khối lượng \(m = 4,{5.10^{ - 6}}g\). Tính vận tốc của hạt mang điện khi nó đập vào bản âm?
Câu 20 :
Fara là điện dung của một tụ điện mà
Câu 21 :
Dòng điện là:
Câu 22 :
Trong nguồn điện lực lạ có tác dụng
Câu 23 :
Suất điện động của một acquy là \(3V\). Lực là dịch chuyển một điện lượng đã thực hiện công là \(6mJ\). Điện lượng dịch chuyển qua acquy đó là
Câu 24 :
Cho đoạn mạch gồm \({R_1}\) mắc song song với \({R_2}\), biểu thức nào sau đây là sai?
Câu 25 :
Cho mạch điện như sau: 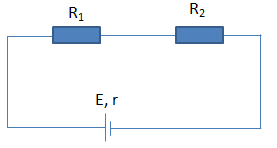 Biết \({R_1} = {R_2} = r\). Cường độ dòng điện chạy trong mạch là:
Lời giải và đáp án
Câu 1 :
Biểu thức xác định định luật Ôm cho đoạn mạch chỉ có điện trở?
Đáp án : A Lời giải chi tiết :
Biểu thức xác định định luật Ôm cho đoạn mạch chỉ có điện trở là: \(I = \frac{U}{R}\)
Câu 2 :
Phát biểu nào sau đây là không đúng?
Đáp án : D Lời giải chi tiết :
A, B, C- đúng D - sai vì: Hiệu điện thế giới hạn là hiệu điện thế lớn nhất đặt vào hai bản tụ điện mà lớp điện môi của tụ điện chưa bị đánh thủng.
Câu 3 :
Một điện tích điểm q = 10-7 C đặt tại điểm M trong điện trường của một điện tích điểm Q, chịu tác dụng của một lực F = 3.10-3 N. Cường độ điện trường do điện tích điểm Q gây ra tại M có độ lớn là bao nhiêu?
Đáp án : C Phương pháp giải :
Áp dụng biểu thức: \(E = \dfrac{F}{{\left| q \right|}}\) Lời giải chi tiết :
Ta có, cường độ điện trường E: \(E = \dfrac{F}{{\left| q \right|}} = \dfrac{{{{3.10}^{ - 3}}}}{{{{10}^{ - 7}}}} = {3.10^4}V/m = {3.10^2}V/cm\)
Câu 4 :
Việc ghép nối tiếp các nguồn điện để
Đáp án : A Lời giải chi tiết :
Suất điện động bộ nguồn khi ghép nối tiếp: Eb = E1 + E2 + E3 +…. + En => Việc ghép nối tiếp các nguồn sẽ có được bộ nguồn có suất điện động lớn hơn các nguồn có sẵn
Câu 5 :
Theo nội dung của thuyết electron, phát biểu nào sau đây là sai?
Đáp án : C Lời giải chi tiết :
A, B, D - đúng C - sai vì nguyên tử nhận thêm electron sẽ trở thành ion âm
Câu 6 :
Cho mạch điện như hình vẽ: E1 = 12V, r1 =1$\Omega $, E2 = 6V, r2 = 2$\Omega $, E3 = 9V, r3 = 3$\Omega $, R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = 3$\Omega $. Hiệu điện thế UAB có giá trị là: 
Đáp án : C Phương pháp giải :
+ Giả sử chiều dòng điện + Áp dụng định luật Ôm cho đoạn mạch Lời giải chi tiết :
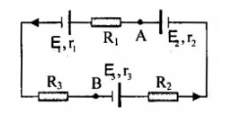 Giả sử chiều các dòng điện trong mạch như hình: Áp dụng định luật Ôm cho mạch kín ta có: \(I = \frac{{{E_2} + {E_3} - {E_1}}}{{{R_1} + {R_2} + {R_3} + {r_1} + {r_2} + {r_3}}} = \frac{{6 + 9 - 12}}{{4 + 2 + 3 + 1 + 2 + 3}} = 0,2A\) Nhận thấy I > 0 => chiều dòng điện giả sử là đúng Hiệu điện thế giữa hai điểm A,B là: \({U_{AB}} = {E_1} + I({R_1} + {R_3} + {r_1}) = 12 + 0,2(4 + 3 + 1) = 13,6V\)
Câu 7 :
Cho mạch điện như hình vẽ: Trong đó: R1 = R2 = 4$\Omega $, R3 = 6$\Omega $, R4 = 3$\Omega $, R5 = 10$\Omega $ Tính điện trở tương đương của đoạn mạch AB? 
Đáp án : B Phương pháp giải :
+ Áp dụng biểu thức xác định điện trở trong mạch nối tiếp: R = R1 + R2 + .... + Rn + Áp dụng biểu thức xác định điện trở trong mạch song song: \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\) Lời giải chi tiết :
Giả sử chiều dòng điện từ A đến B. Ta có: I qua R1 không bị phân nhánh => R1 mắc nối tiếp Tại M, I bị phân nhánh, I’ qua R2, R3 không phân nhánh => (R2 nt R3 ) // R5 I qua R4 không phân nhánh Vậy: đoạn mạch gồm: R1 nt [(R2 nt R3) // R5 ] nt R4 \({R_{23}} = {R_2} + {R_3} = 4 + 6 = 10\Omega \) \(\frac{1}{{{R_{235}}}} = \frac{1}{{{R_{23}}}} + \frac{1}{{{R_5}}} \to {R_{235}} = \frac{{{R_{23}}.{R_5}}}{{{R_{23}} + {R_5}}} = \frac{{10.10}}{{10 + 10}} = 5\Omega \) Tổng trở của toàn mạch: \(R = {R_1} + {R_{235}} + {R_4} = 4 + 5 + 3 = 12\Omega \)
Câu 8 :
Điện tích điểm là:
Đáp án : D Lời giải chi tiết :
Điện tích điểm là một vật tích điện có kích thước rất nhỏ so với khoảng cách điểm mà ta đang xét
Câu 9 :
OA, OB là hai đoạn dây dẫn thẳng, ACB và OBD là hai dây dẫn hình nửa đường tròn đường kính AB và OB. Các đoạn dây dẫn này đồng tính và cùng tiết diện. Biết điện trở của OA và OB bằng nhau và bằng R. Tính điện trở giữa A và B (RAB ) 
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức xác định điện trở của dây dẫn: \(R = \rho \frac{l}{S}\) + Áp dụng tính điện trở tổng cộng Lời giải chi tiết :
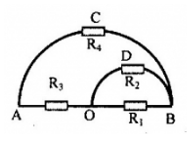 Gọi R1 = ROB = R, R2 = RODB, R3 = RAO = R, R4 = RACB Từ hình vẽ, ta có: ((R1 // R2 ) nối tiếp R3 ) // R4 Ta có, dây dẫn tiết diện đều, đồng tính và điện trở của dây dẫn được xác định bằng biểu thức: \(R = \rho \frac{l}{S}\) \( \to \frac{{{R_2}}}{{{R_1}}} = \frac{{{l_2}}}{{{l_1}}} = \frac{{\pi \left( {\frac{{OB}}{2}} \right)}}{{OB}} \to {R_2} = \frac{{\pi R}}{2}\) Ta có: R4 = 2R2 => R4 = πR + R1//R2 : \({R_{12}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{\frac{{\pi R}}{2}\pi R}}{{\frac{{\pi R}}{2} + \pi R}} = \frac{{\pi R}}{{\pi + 2}}\) + R12 nt R3: \({R_{123}} = {R_{12}} + {R_3} = {R_{12}} = \frac{{\pi R}}{{\pi + 2}} + R = 2R\left( {\frac{{\pi + 1}}{{\pi + 2}}} \right)\) + R123 // R4: \({R_{AB}} = \frac{{{R_{123}}{R_4}}}{{{R_{123}} + {R_4}}} = 2\pi R\left( {\frac{{\pi + 1}}{{{\pi ^2} + 4\pi + 2}}} \right) \approx 1,065R\)
Câu 10 :
Hai điện tích dương q1, q2 có cùng một độ lớn được đặt tại hai điểm A và B, đặt một điện tích q0 vào trung điểm của AB thì ta thấy hệ ba điện tích này nằm cân bằng trong chân không. Bỏ qua trọng lượng của ba điện tích. Chọn kết luận đúng?
Đáp án : C Lời giải chi tiết :
Bỏ qua trọng lượng của 3 điện tích. Vì hai điện tích dương có cùng độ lớn được đặt tại hai điểm A, B và q0 đặt tại trung điểm của AB nên q0 luôn cân bằng do chịu tác dụng của hai lực cùng giá, ngược chiều từ hai điện tích q1, q2.
Để điện tích q1 đặt tại A cân bằng thì lực tác dụng của q0 lên q1 phải cân bằng với lực tác dụng của q2 lên q1, tức ngược chiều lực tác dụng của q2 lên q1. => Vậy q0 phải là điện tích âm
Câu 11 :
Câu phát biểu nào sau đây chưa đúng?
Đáp án : C Lời giải chi tiết :
A, B, D - đúng C - sai vì đường sức điện của điện trường là đường cong không kín
Câu 12 :
Tụ xoay có điện dung thay đổi từ \({C_1} = 30pF\) đến \({C_2} = 120pF\) khi góc xoay biến thiên từ 00 đến 900. Biết điện dung của tụ xoay là hàm bậc nhất của góc xoay . Biểu thức nào sau đây là đúng?
Đáp án : A Lời giải chi tiết :
+ Vì điện dung của tụ là hàm bậc nhất của góc xoay nên ta có: \(C = \alpha a + b\) (a, b là hằng số) + Khi \(\alpha = 0\) thì \({C_1} = 30pF\) và khi \(\alpha = {90^0}\) thì \({C_2} = 120pF\) nên, ta có: \(\left\{ \begin{array}{l}30 = 0{\rm{a}} + b\\120 = 90{\rm{a}} + b\end{array} \right. \to \left\{ \begin{array}{l}a = 1\\b = 30\end{array} \right.\) => Biểu thức của điện dung: \(C = \alpha + 30{\rm{ }}(pF)\)
Câu 13 :
Một quả cầu khối lượng \(m = 4g\) treo bằng một sợi chỉ mảnh. Điện tích của quả cầu là \({q_1} = {2.10^{ - 8}}C\). Phía dưới quả cầu dọc theo phương của sợi chỉ có một điện tích \({q_2}\). Khoảng cách giữa hai điện tích là \(r = 5cm\) và lực căng dây là \(T = {5.10^{ - 2}}N\). Xác định điện tích \({q_2}\) và lực tác dụng giữa chúng, lấy \(g = 10m/{s^2}\)
Đáp án : A Phương pháp giải :
+ Vận dụng tương tác giữa các điện tích + Sử dụng biểu thức tính lực tương tác giữa 2 điện tích: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\) Lời giải chi tiết :
Ta có: + Trọng lượng \(P = mg = \dfrac{4}{{1000}}.10 = 0,04N\) Lực căng dây \(T = {5.10^{ - 2}}N\) Nhận thấy \(T > P \Rightarrow \) lực tương tác giữa hai điện tích phải có chiều như hình vẽ sau: 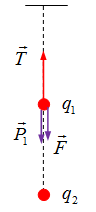 Ta suy ra hai điện tích hút nhau (trái dấu) Lại có \({q_1} > 0 \Rightarrow {q_2} < 0\) \(\overrightarrow T + \overrightarrow P + \overrightarrow F = \overrightarrow 0 \) Chiếu theo phương hướng xuống của sợi dây ta có: \(\begin{array}{l} - T + P + F = 0\\ \Rightarrow F = T - P = {5.10^{ - 2}} - 0,04 = 0,01N\end{array}\) Mặt khác, ta có: \(\begin{array}{l}F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = 0,01N\\ \Rightarrow \left| {{q_2}} \right| = \dfrac{{0,01.0,{{05}^2}}}{{{{9.10}^9}{{.2.10}^{ - 8}}}} = 1,{399.10^{ - 7}}C\end{array}\) \( \Rightarrow {q_2} = - 1,{39.10^{ - 7}}C\) (do điều kiện \({q_2} < 0\) suy ra ở trên)
Câu 14 :
Cho hai điện tích điểm đặt trong chân không. Khi khoảng cách giữa hai điện tích là \(r\) thì lực tương tác điện giữa chúng có độ lớn là \(F\). Khi khoảng cách giữa hai điện tích là \(3r\) thì lực tương tác điện giữa chúng có độ lớn là:
Đáp án : A Phương pháp giải :
Vận dụng biểu thức của định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) Lời giải chi tiết :
Ta có: + Khi khoảng cách giữa hai điện tích điểm là r: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) + Khi khoảng cách giữa hai điện tích điểm là 3r: \(F' = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {{\left( {3r} \right)}^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{9\varepsilon {r^2}}}\) => \(\dfrac{F}{{F'}} = 9 \to F' = \dfrac{F}{9}\)
Câu 15 :
Để xác định điện trở trong r của một nguồn điện, một học sinh mắc mạch điện như hình (H1). Đóng khóa K và điều chỉnh con chạy C, kết quả đo được mô tả bởi đồ thị biểu diễn sự phụ thuộc của số chỉ U của vôn kế V vào số chỉ I của ampe kế A như hình (H2). Điện trở của vôn kế rất lớn. Biết \({R_0} = 2{\rm{0,3 \Omega }}\). Giá trị của r được xác định bởi thí nghiệm này là 
Đáp án : A Phương pháp giải :
Áp dụng công thức: \(U = \xi - I({R_0} + r)\) Lời giải chi tiết :
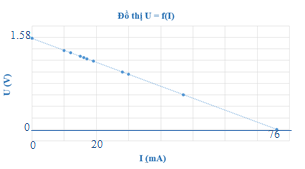 Từ đồ thị ta suy ra: \(1,58 = \xi \) và \(0 = 1,58 - ({{\rm{R}}_{\rm{0}}}{\rm{ + r)}}{\rm{.0,076}}\) \( \Rightarrow {R_0} + r = 20,{\rm{79 (\Omega }}) \Rightarrow r = 0{\rm{,49 (\Omega )}}\)
Câu 16 :
Hai quả cầu nhỏ có điện tích \(2\mu C\) và \(6\mu C\), tương tác với nhau một lực \(0,1N\) trong chân không. Khoảng cách giữa chúng là:
Đáp án : A Phương pháp giải :
Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) Lời giải chi tiết :
Theo định luật Cu-lông, ta có: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) - Đặt trong chân không \( \Rightarrow \varepsilon = 1\) \(\begin{array}{l}F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\ \Rightarrow r = \sqrt {k\dfrac{{\left| {{q_1}{q_2}} \right|}}{F}} = \sqrt {{{9.10}^9}\dfrac{{\left| {{{2.10}^{ - 6}}{{.6.10}^{ - 6}}} \right|}}{{0,1}}} = \dfrac{{3\sqrt 3 }}{5}m\end{array}\)
Câu 17 :
Cường độ điện trường tại một điểm đặc trưng cho:
Đáp án : C Lời giải chi tiết :
Cường độ điện trường \(\overrightarrow E = \dfrac{{\overrightarrow F }}{q}\) là đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu của điện trường tại một điểm.
Câu 18 :
Công thức xác định công của lực điện trường tác dụng lên một điện tích là \(A{\rm{ }} = {\rm{ }}qEd\) , trong đó E là:
Đáp án : B Lời giải chi tiết :
\(A{\rm{ }} = {\rm{ }}qEd\) Trong đó: + d là hình chiếu của quỹ đạo lên phương của đường sức điện. + E - cường độ điện trường + q - điện tích
Câu 19 :
Hai bản kim loại phẳng song song mang điện tích trái dấu được đặt cách nhau \(2cm\). Cường độ điện trường giữa hai bản bằng \(3000V/m\). Sát bề mặt mang điện dương, người ta đặt một hạt mang điện dương \(q = 1,{5.10^{ - 2}}C\), có khối lượng \(m = 4,{5.10^{ - 6}}g\). Tính vận tốc của hạt mang điện khi nó đập vào bản âm?
Đáp án : A Phương pháp giải :
Áp dụng định lí biến thiên động năng: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = {A_{ngoailuc}}\) Lời giải chi tiết :
Ta có, + Điện trường hướng từ bản dương sang bản âm => hạt mang điện dương sẽ chuyển động từ bản dương sang bản âm. + Công của lực điện trường khi hạt di chuyển từ bản dương sang âm. \(A = qEd = 1,{5.10^{ - 2}}.3000.0,02 = 0,9J\) + Khi electron di chuyển từ bản dương đến bản âm thì chịu tác dụng của ngoại lực là lực điện trường nên theo định lí động năng, ta có: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = {A_{ngoailuc}}\) \(\begin{array}{l} \Leftrightarrow \dfrac{1}{2}m{v^2} = 0 = qEd\\ \Rightarrow v = \sqrt {\dfrac{{2qEd}}{m}} = \sqrt {\dfrac{{2.1,{{5.10}^{ - 2}}.3000.0,02}}{{4,{{5.10}^{ - 9}}}}} = 20000m/s = {2.10^4}m/s\end{array}\)
Câu 20 :
Fara là điện dung của một tụ điện mà
Đáp án : A Lời giải chi tiết :
Ta có, điện dung có đơn vị: \(1C/1V = F\) (Fara) Fara là điện dung của một tụ điện mà giữa hai bản tụ có hiệu điện thế 1V thì nó tích được điện tích 1C
Câu 21 :
Dòng điện là:
Đáp án : A Lời giải chi tiết :
Dòng điện là dòng các điện tích (các hạt tải điện) dịch chuyển có hướng.
Câu 22 :
Trong nguồn điện lực lạ có tác dụng
Đáp án : B Lời giải chi tiết :
Ta có: Lực lạ làm dịch chuyển điện tích dương từ cực âm sang cực dương của nguồn điện
Câu 23 :
Suất điện động của một acquy là \(3V\). Lực là dịch chuyển một điện lượng đã thực hiện công là \(6mJ\). Điện lượng dịch chuyển qua acquy đó là
Đáp án : D Phương pháp giải :
Áp dụng biểu thức : \(E{\rm{ }} = \dfrac{A}{q}\) Lời giải chi tiết :
Ta có, \(E{\rm{ }} = \dfrac{A}{q}\) \( \Rightarrow q = \dfrac{A}{E} = \dfrac{{{{6.10}^{ - 3}}}}{3} = {2.10^{ - 3}}\left( C \right)\)
Câu 24 :
Cho đoạn mạch gồm \({R_1}\) mắc song song với \({R_2}\), biểu thức nào sau đây là sai?
Đáp án : B Lời giải chi tiết :
Khi \({R_1}\) mắc song song với \({R_2}\) ta có: \(\begin{array}{l}\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \to R = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\U = {U_1} = {U_2}\\I = {I_1} + {I_2}\\{I_1} = \dfrac{{{U_1}}}{{{R_1}}}\end{array}\) Ta suy ra, các phương án: A, C, D - đúng B - sai
Câu 25 :
Cho mạch điện như sau:  Biết \({R_1} = {R_2} = r\). Cường độ dòng điện chạy trong mạch là:
Đáp án : B Phương pháp giải :
Áp dụng định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) Lời giải chi tiết :
Ta có: \({R_1}nt{R_2}\) Suy ra điện trở tương đương của mạch ngoài: \(R = {R_1} + {R_2} = 2r\) Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{R + r}} = \dfrac{E}{{2r + r}} = \dfrac{E}{{3r}}\) |





















Danh sách bình luận