Đề kiểm tra 1 tiết chương 1: Điện tích - Điện trường - Đề số 02Đề bài
Câu 1 :
Lực tương tác tĩnh điện giữa hai điện tích điểm đứng yên đặt cách nhau một khoảng 4 cm là F. Nếu để chúng cách nhau 1 cm thì lực tương tác giữa chúng là
Câu 2 :
Phát biểu nào sau đây là không đúng?
Câu 3 :
Nguyên tử trung hòa về điện, khi mất bớt electron sẽ trở thành:
Câu 4 :
Hai quả cầu nhỏ có điện tích 10-7 (C) và 4.10-7 (C), tương tác với nhau một lực 0,1 (N) trong chân không. Khoảng cách giữa chúng là:
Câu 5 :
Cường độ điện trường là đại lượng
Câu 6 :
Hiện tượng nào sau đây liên quan đến sự nhiễm điện?
Câu 7 :
Điện tích điểm là:
Câu 8 :
Biểu thức nào sau đây xác định thế năng của một điện tích điểm q tại điểm M trong điện trường?
Câu 9 :
Tìm kết luận không đúng
Câu 10 :
Trong các cách nhiễm điện: I. do cọ xát; II. Do tiếp xúc; III. Do hưởng ứng. Ở cách nào thì tổng đại số điện tích trên vật không thay đổi?
Câu 11 :
Phát biểu nào sau đây về tính chất của các đường sức điện là không đúng?
Câu 12 :
Đặt tại $6$ đỉnh của lục giác đều các điện tích $q$, $-2q$, $3q$, $4q$, $-5q$ và $q'$. Xác định $q'$ theo $q$ để cường độ điện trường tại tâm O của lục giác bằng $0$ biết $q > 0$. 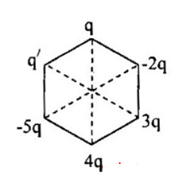
Câu 13 :
Năm tụ giống nhau, mỗi tụ có \(C = 0,2\mu F\) mắc nối tiếp. Bộ tụ được tích điện thu năng lượng \(0,2mJ\). Hiệu điện thế trên mỗi tụ là:
Câu 14 :
Cho \({q_1} = {3.10^{ - 10}}C,{\rm{ }}{q_2} = - {3.10^{ - 10}}C\), đặt tại A và B trong dầu có \(\varepsilon = 2\) biết \(AB = 2{\rm{ }}cm\) . Xác định vectơ \(\vec E\) tại điểm \(H\) - là trung điểm của \(AB\).
Câu 15 :
Một con lắc đơn gồm một quả cầu tích điện dương khối lượng \(\sqrt 3 g\) buộc vào sợi dây mảnh cách điện. Con lắc treo trong điện trường đều có phương nằm ngang với cường độ điện trường \(10000{\rm{ }}V/m\). Tại nơi có \(g = 9,8m/{s^2}\). Khi vật ở vị trí cân bằng, sợi dây lệch một góc \(\alpha = {\rm{ }}{30^0}\) so với phương thẳng đứng. Độ lớn của điện tích của quả cầu là:
Câu 16 :
Nếu tăng khoảng cách giữa hai điện tích điểm lên \(3\) lần thì lực tương tác tĩnh điện giữa chúng sẽ:
Câu 17 :
Đưa một thanh kim loại trung hoà về điện đặt trên một giá cách điện lại gần một quả cầu tích điện âm. Sau khi đưa thanh kim loại ra thật xa quả cầu thì thanh kim loại
Câu 18 :
Hai điện tích \({q_1} = - {2.10^{ - 8}}C\), \({q_2} = - 1,{8.10^{ - 7}}C\) đặt tại A và B trong không khí, \(AB = 8cm\). Một điện tích \({q_3}\) đặt tại C. Hỏi C ở đâu để \({q_3}\) cân bằng?
Câu 19 :
Điện tích thử \(q = - {3.10^{ - 6}}C\) được đặt tại điểm mà tại đó điện trường có phương thẳng đứng, chiều từ trên xuống và có cường độ điện trường \(E = 1,{2.10^4}V/m\). Xác định phương, chiều và độ lớn của lực tác dụng lên điện tích \(q\) ?
Câu 20 :
Tại hai điểm A, B cách nhau \(5cm\) trong chân không có 2 điện tích điểm \({q_1} = {16.10^{ - 10}}C\) và \({q_2} = - {9.10^{ - 10}}C\). Tính cường độ điện trường tổng hợp tại điểm C nằm cách A một khoảng \(4cm\) , cách B một khoảng \(3cm\).
Câu 21 :
Một điện tích q chuyển động trong điện trường không đều theo một đường cong kín. Gọi công của lực điện trong chuyển động đó là
Câu 22 :
Công của lực điện trường dịch chuyển một điện tích \(4\mu C\) dọc theo chiều một đường sức trong một điện trường đều \(1000V/m\) trên quãng đường dài \(1m\) là:
Câu 23 :
Một proton nằm cách electron khoảng \(r = 2,{12.10^{ - 10}}m\) trong chân không. Vận tốc tối thiểu của electron để nó thoát khỏi sức hút của proton là?
Câu 24 :
Fara là điện dung của một tụ điện mà
Câu 25 :
Một electron có động năng \({{\rm{W}}_d} = 200eV\) lúc bắt đầu đi vào điện trường đều của hai bản kim loại đặt song song tích điện trái dấu theo hướng đường sức. Hỏi hiệu điện thế giữa hai bản phải là bao nhiêu để hạt không đến được bản đối diện. Biết \(1eV = 1,{6.10^{ - 19}}J\)
Lời giải và đáp án
Câu 1 :
Lực tương tác tĩnh điện giữa hai điện tích điểm đứng yên đặt cách nhau một khoảng 4 cm là F. Nếu để chúng cách nhau 1 cm thì lực tương tác giữa chúng là
Đáp án : C Phương pháp giải :
Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) Lời giải chi tiết :
Ta có: + Khi r1 = 4cm: Lực tương tác tĩnh điện giữa hai điện tích: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r_1}^2}}\) + Khi r2 = 1cm: Lực tương tác tĩnh điện giữa hai điện tích: \(F' = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r_2}^2}}\) \( \to \dfrac{{F'}}{F} = \dfrac{{r_1^2}}{{r_2^2}} = \dfrac{{{{({{4.10}^{ - 2}})}^2}}}{{{{({{10}^{ - 2}})}^2}}} = 16 \to F' = 16F\)
Câu 2 :
Phát biểu nào sau đây là không đúng?
Đáp án : D Lời giải chi tiết :
A, B, C- đúng D - sai vì: Hiệu điện thế giới hạn là hiệu điện thế lớn nhất đặt vào hai bản tụ điện mà lớp điện môi của tụ điện chưa bị đánh thủng.
Câu 3 :
Nguyên tử trung hòa về điện, khi mất bớt electron sẽ trở thành:
Đáp án : B Lời giải chi tiết :
Nguyên tử trung hòa về điện mà mất electron → trở thành ion +
Câu 4 :
Hai quả cầu nhỏ có điện tích 10-7 (C) và 4.10-7 (C), tương tác với nhau một lực 0,1 (N) trong chân không. Khoảng cách giữa chúng là:
Đáp án : D Phương pháp giải :
Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) Lời giải chi tiết :
Theo định luật Cu-lông, ta có: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) - Đặt trong chân không: => ε = 1 $F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} \to r = \sqrt {k\dfrac{{\left| {{q_1}{q_2}} \right|}}{F}} = \sqrt {{{9.10}^9}\dfrac{{\left| {{{10}^{ - 7}}{{.4.10}^{ - 7}}} \right|}}{{0,1}}} = 0,06m = 6cm$
Câu 5 :
Cường độ điện trường là đại lượng
Đáp án : A Lời giải chi tiết :
Cường độ điện trường là đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu của điện trường tại một điểm Ta có, cường độ điện trường: $\overrightarrow E = \dfrac{{\overrightarrow F }}{q} \to \overrightarrow F = q\overrightarrow E $
Câu 6 :
Hiện tượng nào sau đây liên quan đến sự nhiễm điện?
Đáp án : C Lời giải chi tiết :
Hiện tượng có liên quan đến sự nhiễm điện là hiện tượng sấm sét
Câu 7 :
Điện tích điểm là:
Đáp án : D Lời giải chi tiết :
Điện tích điểm là một vật tích điện có kích thước rất nhỏ so với khoảng cách điểm mà ta đang xét
Câu 8 :
Biểu thức nào sau đây xác định thế năng của một điện tích điểm q tại điểm M trong điện trường?
Đáp án : A Lời giải chi tiết :
Thế năng của một điện tích điểm q tại điểm M trong điện trường: WM = AM∞ = qVM
Câu 9 :
Tìm kết luận không đúng
Đáp án : B Lời giải chi tiết :
Trong sự nhiễm điện do cọ xát, hệ hai vật là hệ cô lập về điện. Theo định luật bảo toàn điện tích, tổng đại số của các điện tích của hai vật không đổi. Lúc đầu tổng đại số của các điện tích của hai vật bằng 0 nên sau khi cọ xát rồi tách ra hai vật sẽ bị nhiễm điện trái dấu, cùng độ lớn
Câu 10 :
Trong các cách nhiễm điện: I. do cọ xát; II. Do tiếp xúc; III. Do hưởng ứng. Ở cách nào thì tổng đại số điện tích trên vật không thay đổi?
Đáp án : C Lời giải chi tiết :
Ở hiện tượng nhiễm điện do hưởng ứng, hai phần của vật nhiễm điện trái dấu có cùng độ lớn, tổng đại số điện tích trên vật không thay đổi
Câu 11 :
Phát biểu nào sau đây về tính chất của các đường sức điện là không đúng?
Đáp án : C Lời giải chi tiết :
A, B, D - đúng C - sai vì: Nơi nào cường độ điện trường lớn hơn thì các đường sức điện ở đó được vẽ mau hơn (dày hơn), nơi nào cường độ điện trường nhỏ hơn thì các đường sức điện ở đó được vẽ thưa hơn.
Câu 12 :
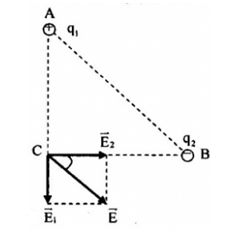
Đặt tại $6$ đỉnh của lục giác đều các điện tích $q$, $-2q$, $3q$, $4q$, $-5q$ và $q'$. Xác định $q'$ theo $q$ để cường độ điện trường tại tâm O của lục giác bằng $0$ biết $q > 0$. 
Đáp án : B Phương pháp giải :
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \) + Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\) Lời giải chi tiết :
Gọi + \(\overrightarrow {{E_{3q}}} \) là điện trường tổng hợp tại O do $q$ và $4q$ gây ra. + \(\overrightarrow {{E_{ - 3q}}} \) là điện trường tổng hợp tại O do $-5q$ và $-2q$ gây ra. + \(\overrightarrow {{E_3}} \) là điện trường tổng hợp tại O do $q$ và $4q$ gây ra. Các véctơ được biểu diễn như hình. 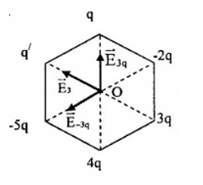 Ta có: \(\overrightarrow {{E_0}} = \overrightarrow {{E_{ - 3q}}} + \overrightarrow {{E_{3q}}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{ - 33}}} + \overrightarrow {{E_3}} \) Vì => \(\overrightarrow {{E_{ - 33}}} \) cùng chiều \(\overrightarrow {{E_3}} \) Ta có: \(\left\{ \begin{array}{l}{E_{ - 33}} = {E_3}\\\overrightarrow E = \overrightarrow {{E_{ - 33}}} + \overrightarrow {{E_3}} \end{array} \right. \to E = 2{E_3} = 2k\frac{{3q}}{{{r^2}}} = k\frac{{6q}}{{{r^2}}}\) Để tại O cường độ điện trường tổng hợp bằng 0 thì: \(\overrightarrow {{E_{q'}}} + \overrightarrow E = 0 \to \left\{ \begin{array}{l}\overrightarrow {{E_{q'}}} \uparrow \downarrow \overrightarrow E \to q' > 0\\{E_{q'}} = E \leftrightarrow k\dfrac{{\left| {q'} \right|}}{{{r^2}}} = k\dfrac{{6q}}{{{r^2}}} \to \left| {q'} \right| = 6q\end{array} \right. \to q' = 6q\)
Câu 13 :
Năm tụ giống nhau, mỗi tụ có \(C = 0,2\mu F\) mắc nối tiếp. Bộ tụ được tích điện thu năng lượng \(0,2mJ\). Hiệu điện thế trên mỗi tụ là:
Đáp án : B Phương pháp giải :
+ Vận dụng biểu thức tính điện dung của bộ tụ khi mắc nối tiếp: \(\frac{1}{{{C_b}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + ... + \frac{1}{{{C_n}}}\) + Vận dụng biểu thức tính năng lượng của tụ điện: \({\rm{W}} = \frac{1}{2}C{U^2}\) + Vận dụng biểu thức xác định hiệu điện thế khi mắc các tụ nối tiếp: \(U = {U_1} + {U_2} + \ldots + {U_n}\) Lời giải chi tiết :
Ta có: + Điện dung của bộ 5 tụ nối tiếp: \(\begin{array}{l}\frac{1}{{{C_b}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + \frac{1}{{{C_3}}} + \frac{1}{{{C_4}}} + \frac{1}{{{C_5}}} = \frac{5}{C}\\ \to {C_b} = \frac{C}{5} = \frac{{0,2}}{5} = 0,04\mu F\end{array}\) + Năng lượng của bộ tụ: \({\rm{W}} = \frac{1}{2}{C_b}{U^2} \to U = \sqrt {\frac{{2{\rm{W}}}}{{{C_b}}}} = \sqrt {\frac{{2.0,{{2.10}^{ - 3}}}}{{0,{{04.10}^{ - 6}}}}} = 100V\) Vì 5 tụ mắc nối tiếp, nên: \(\begin{array}{l}U = {U_1} + {U_2} + {U_3} + {U_4} + {U_5} = 5{U_1}\\ \to {U_1} = \frac{U}{5} = \frac{{100}}{5} = 20V\end{array}\)
Câu 14 :
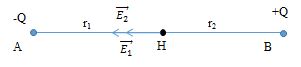
Cho \({q_1} = {3.10^{ - 10}}C,{\rm{ }}{q_2} = - {3.10^{ - 10}}C\), đặt tại A và B trong dầu có \(\varepsilon = 2\) biết \(AB = 2{\rm{ }}cm\) . Xác định vectơ \(\vec E\) tại điểm \(H\) - là trung điểm của \(AB\).
Đáp án : A Phương pháp giải :
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \) + Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\) Lời giải chi tiết :
- Gọi cường độ điện trường do \({q_1}\) gây ra là $E_1$; do $q_2$ gây ra là $E_2$ - Theo nguyên lí chồng chất điện trường:\(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
Vì \({E_1},{\rm{ }}{E_2}\) là 2 véc tơ cùng phương, cùng chiều nên: \(E{\rm{ }} = {\rm{ }}{E_1} + {\rm{ }}{E_2}\) Ta có, cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\) Thay \({q_1} = {3.10^{ - 10}}C,{\rm{ }}{q_2} = - {3.10^{ - 10}}C,{\rm{ }}{r_1} = {\rm{ }}{r_2} = 1cm{\rm{ }},\varepsilon = 2\) Ta có: \( \to E = 2.{E_1} = 27.{\rm{ }}{10^3}V/m\)
Câu 15 :
Một con lắc đơn gồm một quả cầu tích điện dương khối lượng \(\sqrt 3 g\) buộc vào sợi dây mảnh cách điện. Con lắc treo trong điện trường đều có phương nằm ngang với cường độ điện trường \(10000{\rm{ }}V/m\). Tại nơi có \(g = 9,8m/{s^2}\). Khi vật ở vị trí cân bằng, sợi dây lệch một góc \(\alpha = {\rm{ }}{30^0}\) so với phương thẳng đứng. Độ lớn của điện tích của quả cầu là:
Đáp án : C Phương pháp giải :
+ Xác định các lực tác dụng lên vật + Áp dụng điều kiện cân bằng của vật + Áp dụng biểu thức tính lực điện: \(F{\rm{ }} = {\rm{ }}qE\) + Vận dụng công thức lượng giác. Lời giải chi tiết :
Các lực tác dụng lên quả cầu gồm: lực điện \(\overrightarrow F \) , trọng lực \(\overrightarrow P \)hướng xuống và lực căng dây \(\overrightarrow T \). Khi quả cầu cân bằng: \(\overrightarrow T + \overrightarrow P + \overrightarrow F = 0 \to \overrightarrow T + \overrightarrow {P'} = 0\) => $P'$ có phương sợi dây $P'$ tạo với $P$ một góc \(\alpha {\rm{ }} = {\rm{ }}{30^0}\) 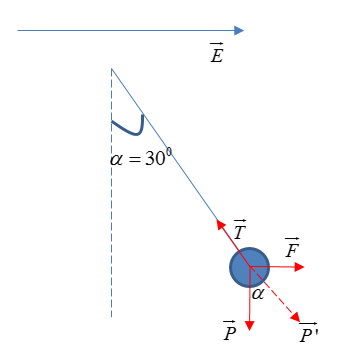 Từ hình ta có: \(\tan \alpha = \dfrac{F}{P} = \dfrac{{\left| q \right|E}}{{mg}} = \tan {30^0} \to \left| q \right| = \dfrac{{mg\tan {{30}^0}}}{E} = \dfrac{{\sqrt 3 {{.10}^{ - 3}}.9,8.\tan {{30}^0}}}{{10000}} = {9,8.10^{ - 7}}C\)
Câu 16 :
Nếu tăng khoảng cách giữa hai điện tích điểm lên \(3\) lần thì lực tương tác tĩnh điện giữa chúng sẽ:
Đáp án : C Phương pháp giải :
Sử dụng biểu thức tính lực tương tác tĩnh điện: $F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}$ Lời giải chi tiết :
Ta có lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) Nhận thấy \(F \sim \frac{1}{{{r^2}}}\) => Khi tăng khoảng cách giữa hai điện tích điểm lên \(3\) lần thì lực tương tác tĩnh điện giữa chúng sẽ giảm \(9\) lần
Câu 17 :
Đưa một thanh kim loại trung hoà về điện đặt trên một giá cách điện lại gần một quả cầu tích điện âm. Sau khi đưa thanh kim loại ra thật xa quả cầu thì thanh kim loại
Đáp án : D Lời giải chi tiết :
Ta có, khi đưa thanh kim loại ra thật xa quả cầu thì thanh kim loại trở về trạng thái không nhiễm điện như lúc đầu tức là trung hòa về điện
Câu 18 :
Hai điện tích \({q_1} = - {2.10^{ - 8}}C\), \({q_2} = - 1,{8.10^{ - 7}}C\) đặt tại A và B trong không khí, \(AB = 8cm\). Một điện tích \({q_3}\) đặt tại C. Hỏi C ở đâu để \({q_3}\) cân bằng?
Đáp án : C Phương pháp giải :
+ Áp dụng biểu thức định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\) + Vận dụng phương pháp tổng hợp lực + Vận dụng điều kiện cân bằng của vật Lời giải chi tiết :
Gọi \(\overrightarrow {{F_{13}}} ,\overrightarrow {{F_{23}}} \) lần lượt là lực do \({q_1},{q_2}\) tác dụng lên \({q_3}\) + Điều kiện cân bằng của \({q_3}\): \(\overrightarrow {{F_{12}}} + \overrightarrow {{F_{23}}} = \overrightarrow 0 \) \( \Rightarrow \overrightarrow {{F_{13}}} = - \overrightarrow {{F_{23}}} \) \( \Rightarrow \) điểm C phải thuộc AB + Vì \({q_1}\) và \({q_2}\) cùng dấu nên ta suy ra C phải nằm trong AB + Lại có \({F_{13}} = {F_{23}}\) \(\begin{array}{l} \Leftrightarrow k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{C{A^2}}} = k\dfrac{{\left| {{q_2}{q_3}} \right|}}{{C{B^2}}}\\ \Rightarrow \dfrac{{{q_1}}}{{C{A^2}}} = \dfrac{{{q_2}}}{{C{B^2}}}\\ \Rightarrow \dfrac{{CB}}{{CA}} = \sqrt {\dfrac{{{q_2}}}{{{q_1}}}} = \sqrt {\dfrac{{ - 1,{{8.10}^{ - 7}}}}{{ - {{2.10}^{ - 8}}}}} = 3\end{array}\) \( \Rightarrow CB = 3CA\) (1) \( \Rightarrow \) C gần A hơn + Mặt khác, ta có: \(CA + CB = 8cm\) (2) Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}CA = 2cm\\CB = 6cm\end{array} \right.\)
Câu 19 :
Điện tích thử \(q = - {3.10^{ - 6}}C\) được đặt tại điểm mà tại đó điện trường có phương thẳng đứng, chiều từ trên xuống và có cường độ điện trường \(E = 1,{2.10^4}V/m\). Xác định phương, chiều và độ lớn của lực tác dụng lên điện tích \(q\) ?
Đáp án : C Phương pháp giải :
+ Vận dụng phương pháp xác định phương, chiều của cường độ điện trường + Áp dụng biểu thức xác định cường độ điện trường E: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\) Lời giải chi tiết :
Ta có: \(\overrightarrow F = q\overrightarrow E \) Ta suy ra \(F = \left| q \right|E = \left| { - {{3.10}^{ - 6}}} \right|.1,{2.10^4} = 0,036N\) Do \(q < 0\) nên lực \(\overrightarrow F \) có phương thẳng đứng, chiều ngược với chiều của \(\overrightarrow E \). Vậy, \(F = 0,036N\) có phương thẳng đứng, chiều hướng từ dưới lên.
Câu 20 :
Tại hai điểm A, B cách nhau \(5cm\) trong chân không có 2 điện tích điểm \({q_1} = {16.10^{ - 10}}C\) và \({q_2} = - {9.10^{ - 10}}C\). Tính cường độ điện trường tổng hợp tại điểm C nằm cách A một khoảng \(4cm\) , cách B một khoảng \(3cm\).
Đáp án : C Phương pháp giải :
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \) + Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\) Lời giải chi tiết :
Nhận thấy \(A{B^2} = A{C^2} + C{B^2} = {5^2}\) \( \Rightarrow \) tam giác \(ABC\) vuông tại \(C\) Gọi \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} \) lần lượt là cường độ điện trường do điện tích \({q_1},{q_2}\) gây ra tại C. Các véc-tơ \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} \) được biểu diễn như hình.
Ta có: \(\left\{ \begin{array}{l}{E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{r_1^2}} = k\dfrac{{\left| {{q_1}} \right|}}{{A{C^2}}} = {9.10^9}\dfrac{{{{16.10}^{ - 10}}}}{{0,{{04}^2}}} = 9000V/m\\{E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{r_2^2}} = k\dfrac{{\left| {{q_2}} \right|}}{{C{B^2}}} = {9.10^9}\dfrac{{{{9.10}^{ - 10}}}}{{0,{{03}^2}}} = 9000V/m\end{array} \right.\) Gọi \(\overrightarrow E \) là véc tơ cường độ điện trường tổng hợp tại \(C\). Ta có: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \) Vì \(\overrightarrow {{E_1}} \bot \overrightarrow {{E_2}} \) \( \Rightarrow E = \sqrt {E_1^2 + E_2^2} = \sqrt {{{9000}^2} + {{9000}^2}} = 9000\sqrt 2 V/m\)
Câu 21 :
Một điện tích q chuyển động trong điện trường không đều theo một đường cong kín. Gọi công của lực điện trong chuyển động đó là
Đáp án : D Lời giải chi tiết :
Ta có công của lực điện không phụ thuộc dạng đường đi mà chỉ phụ thuộc vào điểm đầu và điểm cuối của đường đi trong điện trường Theo đề bài, ta có: điện tích q chuyển động theo một đường cong kín => Công của lực điện trong chuyển động đó A = 0
Câu 22 :
Công của lực điện trường dịch chuyển một điện tích \(4\mu C\) dọc theo chiều một đường sức trong một điện trường đều \(1000V/m\) trên quãng đường dài \(1m\) là:
Đáp án : C Phương pháp giải :
Áp dụng công thức xác định công của lực điện: \({A_\;} = \;qEd\) Lời giải chi tiết :
Ta có, công của lực điện tác dụng lên điện tích dịch chuyển trong điện trường: \(A = qEd = {4.10^{ - 6}}.1000.1 = {4.10^{ - 3}}J = 4mJ\)
Câu 23 :
Một proton nằm cách electron khoảng \(r = 2,{12.10^{ - 10}}m\) trong chân không. Vận tốc tối thiểu của electron để nó thoát khỏi sức hút của proton là?
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức tính thế năng tương tác tĩnh điện: \({\rm{W}} = k\dfrac{{{e^2}}}{r}\) + Áp dụng biểu thức tính động năng: \({\rm{W}} = \dfrac{1}{2}m{v^2}\) + Áp dụng định luật bảo toàn năng lượng Lời giải chi tiết :
Ta có: + Lúc đầu năng lượng của hệ là thế năng tương tác tĩnh điện: \({{\rm{W}}_1} = k\dfrac{{{e^2}}}{r}\) + Khi nó vừa thoát ra thì có vận tốc v, lúc này nó không chịu lực hút của proton nên lúc này hệ không còn thế năng tương tác mà chỉ có động năng: \({{\rm{W}}_2} = \dfrac{1}{2}m{v^2}\) Áp dụng định luật bảo toàn năng lượng, ta có: \(\begin{array}{l}{{\rm{W}}_1} = {{\rm{W}}_2} \leftrightarrow k\dfrac{{{e^2}}}{r} = \dfrac{1}{2}m{v_0}^2\\ \to {v_0} = \sqrt {k\dfrac{{2{{\rm{e}}^2}}}{{m{\rm{r}}}}} = \sqrt {{{9.10}^9}\dfrac{{2.{{\left( {1,{{6.10}^{ - 19}}} \right)}^2}}}{{9,{{1.10}^{ - 31}}.2,{{12.10}^{ - 10}}}}} = 1,{545.10^6}m/s\end{array}\)
Câu 24 :
Fara là điện dung của một tụ điện mà
Đáp án : A Lời giải chi tiết :
Ta có, điện dung có đơn vị: \(1C/1V = F\) (Fara) Fara là điện dung của một tụ điện mà giữa hai bản tụ có hiệu điện thế 1V thì nó tích được điện tích 1C
Câu 25 :
Một electron có động năng \({{\rm{W}}_d} = 200eV\) lúc bắt đầu đi vào điện trường đều của hai bản kim loại đặt song song tích điện trái dấu theo hướng đường sức. Hỏi hiệu điện thế giữa hai bản phải là bao nhiêu để hạt không đến được bản đối diện. Biết \(1eV = 1,{6.10^{ - 19}}J\)
Đáp án : A Phương pháp giải :
+ Sử dụng định lí biến thiên động năng: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = {A_{ngoailuc}}\) + Sử dụng biểu thức liên hệ giữa cường độ điện trường và hiệu điện thế: \(E = \dfrac{U}{d}\) Lời giải chi tiết :
Khi electron chuyển động từ bản này đến bản kia, thì nó chịu tác dụng của ngoại lực là lực điện trường. + Theo định lí động năng, ta có: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = qE{d_{12}}\) \( \Rightarrow {d_{12}} = \dfrac{{ - {{\rm{W}}_{{d_1}}}}}{{qE}} = \dfrac{{ - 200.1,{{6.10}^{ - 19}}}}{{ - 1,{{6.10}^{ - 19}}.E}} = \dfrac{{200}}{E}\) + Để electron không đến được bản đối diện thì quãng đường nó đi được phải nhỏ hơn khoảng cách giữa hai bản này hay \({d_{12}} < d\) (1) Lại có: \(d = \dfrac{U}{E}\) (2) Từ (1) và (2) ta suy ra: \(\dfrac{{200}}{E} < \dfrac{U}{E} \Rightarrow U > 200V\) |




















Danh sách bình luận