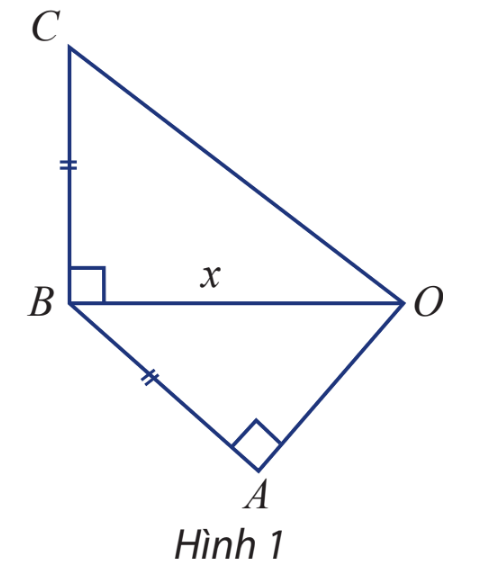
Giải mục 2 trang 16, 17 SGK Toán 10 tập 2 - Chân trời sáng tạoCho tam giác OAB và OBC lần lượt vuông tại A và B như hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1 cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
HĐ Khám phá 2 Lời giải cho phương trình \(\sqrt { - {x^2} + x + 1} = x\) như sau đúng hai sai? \(\)\(\sqrt { - {x^2} + x + 1} = x\) \( \Rightarrow - {x^2} + x + 1 = {x^2}\) (bình phương cả hai vế để làm mất dấu căn) \( \Rightarrow - 2{x^2} + x + 1 = 0\) (chuyển vế, rút gọn) \( \Rightarrow x = 1\) hoặc \(x = - \frac{1}{2}\) (giải phương trình bậc hai) Vậy phương trình đã cho có hai nghiệm là 1 và \( - \frac{1}{2}\) Phương pháp giải: Thay nghiệm tìm được vào phương trình ban đầu ta có: +) Thay \(x = 1\) vào phương trình \(\sqrt { - {x^2} + x + 1} = x\) ta thấy thảo mãn phương trình +) Thay \(x = - \frac{1}{2}\) vào \(\sqrt { - {x^2} + x + 1} = x\) ta thấy không thỏa mãn phương trình Vậy nghiệm của phương trình là \(x = 1\), suy ra lời giải như trên là sai. Thực hành 2 Giải phương trình \(\sqrt {3{x^2} + 27x - 41} = 2x + 3\) Phương pháp giải: Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn Bước 3: Giải phương trình nhận được ở bước 2 Bước 4: Thử lại và kết luận Lời giải chi tiết: Bình phương hai vế của phương trình đã cho, ta được: \(3{x^2} + 27x - 41 = {\left( {2x + 3} \right)^2}\) \( \Rightarrow 3{x^2} + 27x - 41 = 4{x^2} + 12x + 9\) \( \Rightarrow {x^2} - 15x + 50 = 0\) \( \Rightarrow x = 5\) và \(x = 10\) Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {3{x^2} + 27x - 41} = 2x + 3\) ta thấy cả hai nghiệm đều thỏa mãn phương trình Vậy nghiệm của phương trình đã cho là \(x = 5\) và \(x = 10\) Vận dụng Cho tam giác OAB và OBC lần lượt vuông tại A và B như hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1 cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để: a) \(OC = 3OA;\) b) \(OC = \frac{5}{4}OB\)
Phương pháp giải: Bước 1: Sử dụng giả thiết và áp dụng định lý pitago để biểu diễn độ dài OC và OA qua OB Bước 2: Lập phương trình theo giả thiết \(OC = 3OA;\)\(OC = \frac{5}{4}OB\) Bước 3: Giải phương trình Lời giải chi tiết: Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\) Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\) Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có: \(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \) \(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \) a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) \(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\) \( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \) Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\) b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) \(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\) \( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\) Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)
|




















Danh sách bình luận