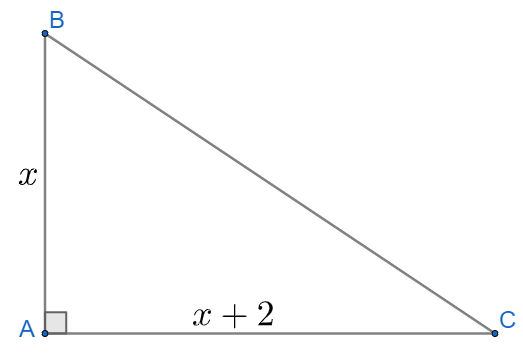
Giải bài 3 trang 17 SGK Toán 10 tập 2 – Chân trời sáng tạoCho tam giác ABC vuông tại A có AB ngắn hơn AC là 2 cm. a) Biểu diễn độ dài cạnh huyền BC theo AB b) Biết chu vi của tam giác ABC là 24 cm. Tính độ dài ba cạnh của tam giác đó. Quảng cáo
Đề bài Cho tam giác ABC vuông tại A có AB ngắn hơn AC là 2 cm. a) Biểu diễn độ dài cạnh huyền BC theo AB b) Biết chu vi của tam giác ABC là 24 cm. Tính độ dài ba cạnh của tam giác đó. Phương pháp giải - Xem chi tiết a) Bước 1: Đặt độ dài cạnh AB là x (\(x > 0\)), biểu diễn AC theo AB Bước 2: Áp dụng định lý Pitago biểu diễn cạnh BC b) Bước 1: Lập biểu thức tính chu vi của tam giác Bước 2: Giải phương trình vừa tìm được Lời giải chi tiết
a) Đặt độ dài cạnh AB là x (\(x > 0\)) Theo giả thiết ta có độ dài \(AC = AB + 2 = x + 2\) Áp dụng định lý pitago trong tam giác vuông ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{x^2} + {{\left( {x + 2} \right)}^2}} = \sqrt {2{x^2} + 4x + 4} \) b) Chu vi của tam giác là \(C = AB + AC + BC\) \( \Rightarrow C = x + \left( {x + 2} \right) + \sqrt {2{x^2} + 4x + 4} = 2x + 2 + \sqrt {2{x^2} + 4x + 4} \) Theo giả thiết ta có \(\begin{array}{l}C = 24 \Leftrightarrow 2x + 2 + \sqrt {2{x^2} + 4x + 4} = 24\\ \Leftrightarrow \sqrt {2{x^2} + 4x + 4} = 22 - 2x\\ \Rightarrow 2{x^2} + 4x + 4 = {\left( {22 - 2x} \right)^2}\\ \Rightarrow 2{x^2} + 4x + 4 = 4{x^2} - 88x + 484\\ \Rightarrow 2{x^2} - 92x + 480 = 0\end{array}\) \( \Rightarrow x = 6\) hoặc \(x = 40\) Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} + 4x + 4} = 22 - 2x\) ta thấy chỉ có \(x = 6\) thỏa mãn phương trình Vậy độ dài ba cạnh của tam giác là \(AB = 6;AC = 8\) và \(BC = 10\)(cm)
|




















Danh sách bình luận