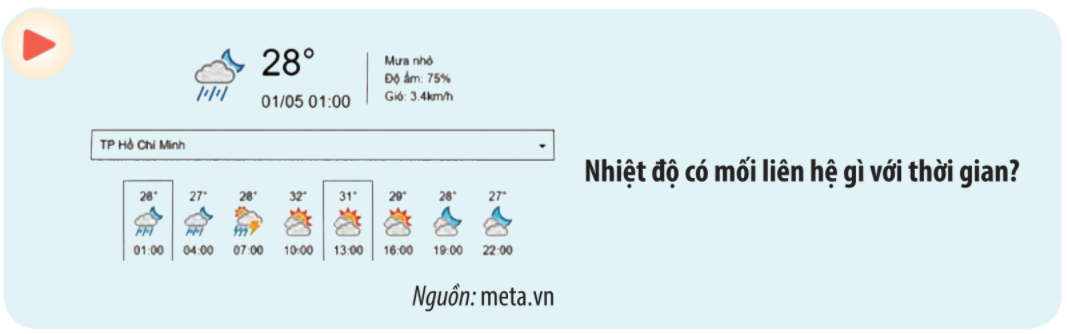
Giải mục 1 trang 41, 42, 43 SGK Toán 10 tập 1 - Chân trời sáng tạoBản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 01/5/2021 tại thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên. Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
HĐ Khởi động
Lời giải chi tiết: Mỗi thời điểm (giờ) chỉ có một nhiệt độ dự báo nhất định. Nhiệt độ dự báo là một đại lượng phụ thuộc vào thời điểm (giờ). Mối liên hệ giữa hai đại lượng này (nhiệt độ và thời gian) có đặc trưng của một hàm số. HĐ Khám phá 1 Bản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 01/5/2021 tại thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên.
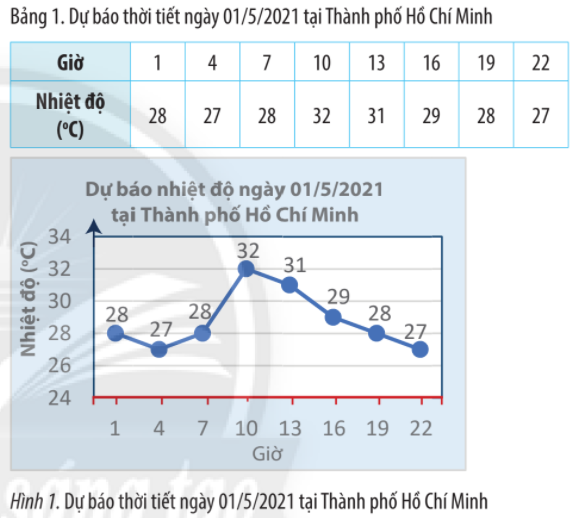
Sử dụng bảng hoặc biểu đồ, hãy: a) Viết tập hợp các mốc đã có dự báo nhiệt độ. b) Viết tập hợp các số đo nhiệt độ đã dự báo. c) Cho biết nhiệt độ dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021. Lời giải chi tiết: a) Tập hợp các mốc giờ đã có dự báo nhiệt độ là: \(A = \{ 1;4;7;10;13;16;19;22\} \) b) Tập hợp các số đo nhiệt độ đã dự báo là: \(B = \{ 28;27;32;31;29\} \) c) Dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021 nhiệt độ là \({28^o}C.\) Thực hành 1 Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
Vì sao bảng này biểu thị một hàm số? Tìm tập xác định của hàm số này. Phương pháp giải: Ta gọi y là hàm số của biến số x nếu với mỗi giá trị x thuộc D, ta xác định được một và chỉ một giá trị tương ứng y thuộc tập hợp số thực \(\mathbb{R}\). Tập D được gọi là tập xác định. Lời giải chi tiết: Từ bảng giá trị vận tốc v (mét/giây) ở thời điểm t (giây) của vật chuyển động, ta thấy ứng với mỗi thời điểm t (giây) trong bảng đều có một giá trị vận tốc v duy nhất. Vì vậy, bảng này biểu thị một hàm số. Hàm số đó có tập xác định \(D = \{ 0,5;1;1,2;1,8;2,5\} \) Thực hành 2 Tìm tập xác định của các hàm số sau: a) \(f(x) = \sqrt {2x + 7} \) b) \(f(x) = \frac{{x + 4}}{{{x^2} - 3x + 2}}\) Phương pháp giải: Tập xác định của hàm số \(y = f(x)\) là tập hợp tất cả các số thực x sao cho biểu thức \(f(x)\) có nghĩa. a) \(\sqrt A \) có nghĩa \( \Leftrightarrow A \ge 0\) b) \(\frac{A}{B}\) có nghĩa \( \Leftrightarrow B \ne 0\) Lời giải chi tiết: a) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(2x + 7 \ge 0,\)tức là khi \(x \ge \frac{{ - 7}}{2}.\) Vậy tập xác định của hàm số này là \(D = \left[ { - \frac{7}{2}; + \infty )} \right.\) b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \({x^2} - 3x + 2 \ne 0,\)tức là khi \(x \ne 2,x \ne 1.\) Vậy tập xác định của hàm số này là \(D = \mathbb{R}\backslash \left\{ {1;2} \right\}\) Vận dụng Ở góc của miếng đất hình chữ nhật, người ta làm một bồn hoa có dạng một phần tư hình tròn với bán kính r (Hình 2). Bán kính bồn hoa có kích thước từ 0,5 m đến 3 m.
a) Viết công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r và tìm tập xác định của hàm số này. b) Bán kính bồn hoa bằng bao nhiêu thì nó có diện tích là \(0,5\pi \;{m^2}?\) Phương pháp giải: a) Diện tích hình tròn \(S = \pi {r^2}\) Gọi x là biến số thể hiện kích thước của bán kính, từ đó suy ra công thức hàm số tính diện tích bồn hoa (một phần tư hình tròn) theo x. Tập xác định là tập hợp các kích thước của bán kính bồn hoa. b) Cho \(f(x) = 0,5\pi \;({m^2})\), tìm x. Lời giải chi tiết: a) Diện tích một phần tư hình tròn là: \(\frac{1}{4}\pi {r^2}\) Gọi x là biến số thể hiện kích thước của bán kính. Công thức hàm số tính diện tích bồn hoa là: \(f(x) = \frac{1}{4}\pi {x^2}\) +) Vì bán kính bồn hoa có kích thước từ 0,5 m đến 3 m nên \(0,5 \le x \le 3\) Vậy tập xác định của hàm số này là \(D = [0,5;3]\) b) Diện tích là \(0,5\pi \;{m^2}\) tức là\(f(x) = 0,5\pi \;\) \( \Leftrightarrow \frac{1}{4}\pi {x^2} = 0,5\pi \Leftrightarrow {x^2} = 2 \Rightarrow x = \sqrt 2 \) (do \(0,5 \le x \le 3\)) Vậy bán kính bồn hoa bằng \(\sqrt 2 \;m\).
|





















Danh sách bình luận