Giải bài 17 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạoCổng trời của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc kẻ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng Quảng cáo
Đề bài Cổng trời của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc kẻ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng
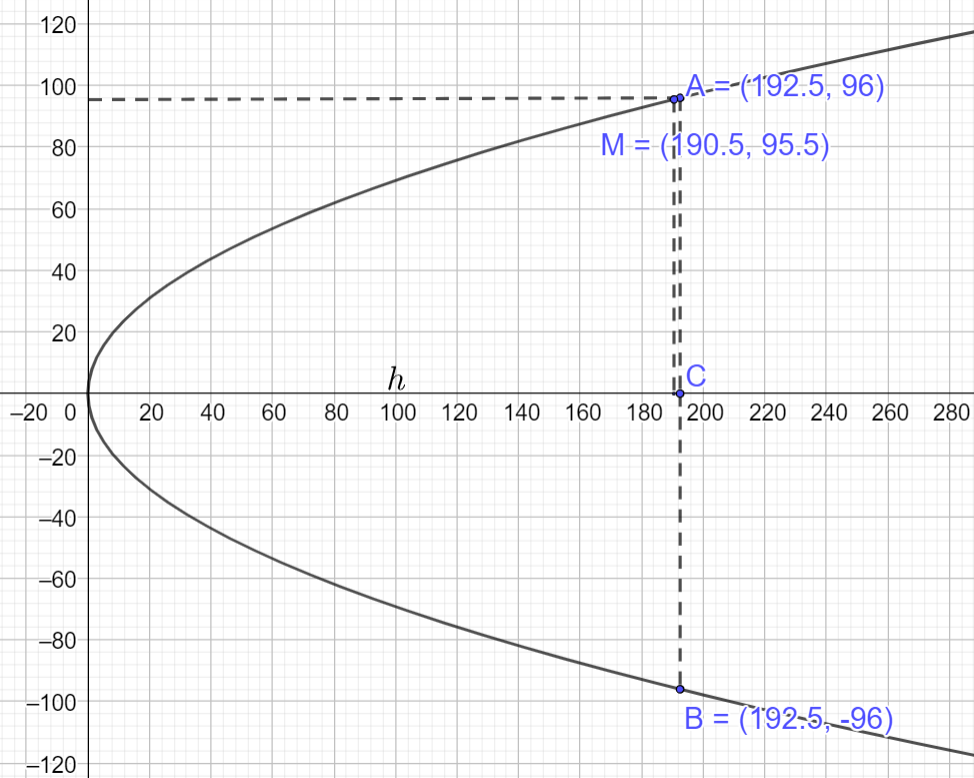
Phương pháp giải - Xem chi tiết Bước 1: Gắn hệ trục tọa độ Oxy Bước 2: Gọi phương trình chính tắc mô phỏng cổng là \({y^2} = 2px\) Bước 3: Thay điểm M vào phương trình, xác định phương trình parabol Bước 4: Xác định chiều cao của cổng Lời giải chi tiết Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\) Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có: \(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\) Vậy chiều cao của cổng gần bằng 192,5 m
|




















Danh sách bình luận