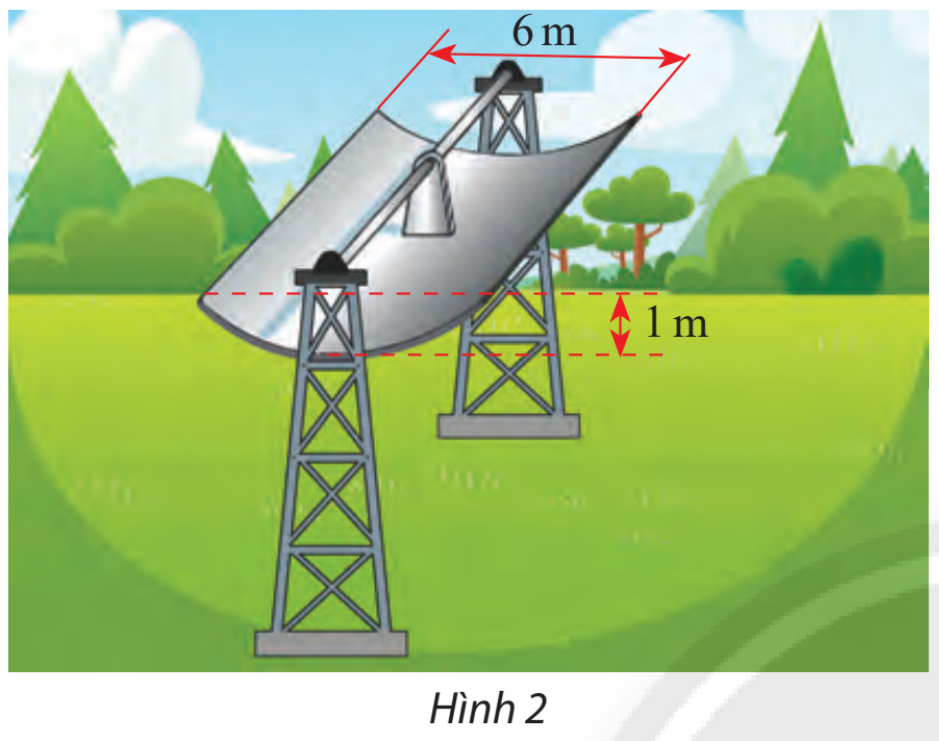
Giải bài 16 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạoMột bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol (hình 2). Nước sẽ chảy thông qua một đường ống nằm ở tiêu điểm của parabol Quảng cáo
Đề bài Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol (hình 2). Nước sẽ chảy thông qua một đường ống nằm ở tiêu điểm của parabol a) Viết phương trình chính tắc của parabol b) Tính khoảng cách từ tâm đường ống đến đỉnh của parabol
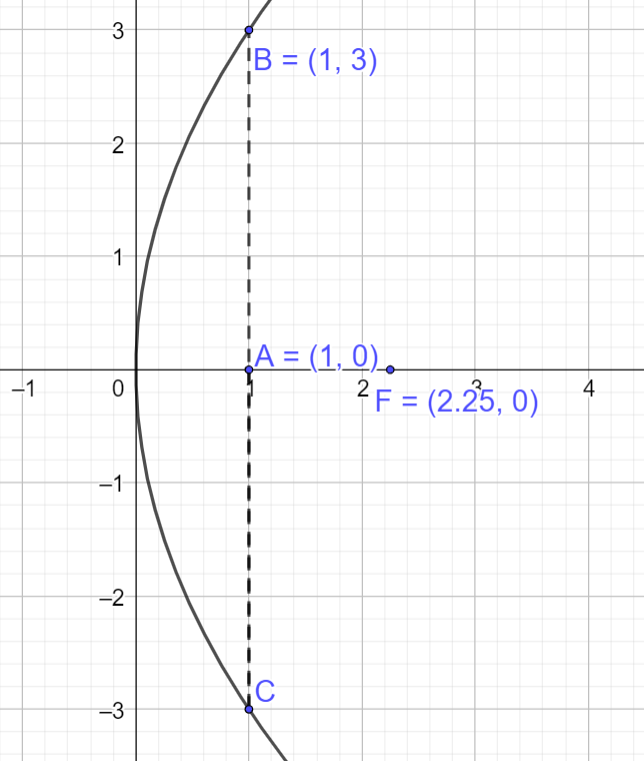
Phương pháp giải - Xem chi tiết a) Bước 1: Xác định điểm nằm trên đường parabol Bước 2: Giả sử phương trình của parabol là \({y^2} = 2px\), thay tọa độ điểm vừa tìm được tìm p Bước 3: Xác định phương trình chính tắc của parabol b) Xác định tọa độ của tiêu điểm \(F\left( {\frac{p}{2};0} \right)\) Lời giải chi tiết a) Vẽ lại parabol mô phỏng mặt cắt trên như hình dưới
Ta có: \(OA = 1,BC = 2{y_B} = 6 \Rightarrow B\left( {1;3} \right)\) Giả sử phương trình chính tắc của parabol có dạng \({y^2} = 2px\) Thay tọa độ điểm B vào phương trình \({y^2} = 2px\) ta có: \({3^2} = 2p.1 \Rightarrow p = \frac{9}{2}\) Vậy phương trình chính tắc của parabol mô phỏng mặt cắt trên là \({y^2} = 9x\) b) Khoảng cách từ tâm đường ống đến đỉnh của parabol chính là độ dài từ đỉnh tới tiêu điểm của parabol Từ phương trình chính tắc ta có tiêu điểm \(F\left( {\frac{9}{4};0} \right)\) Vậy khoảng cách từ tâm đường ống đến đỉnh của parabol là \(\frac{9}{4}\) m
|




















Danh sách bình luận