Giải mục 4 trang 54, 55 SGK Toán 10 tập 1 - Chân trời sáng tạoTrong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được xem là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên) a) Vận tốc xuất phát của cầu là 12 m/s b) Vị trí phát cầu cách mặt đất 1,3 m. Lưu ý: Các thông số về sân cầu lông đơn được cho trong Hình 11. Tổng hợp đề thi giữa kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
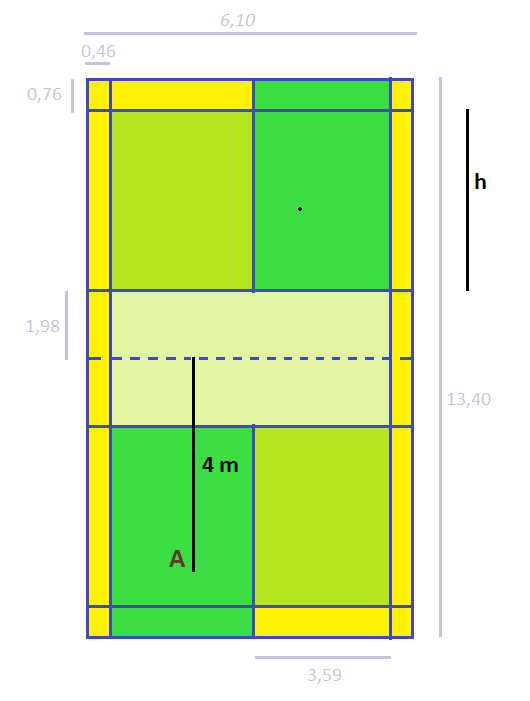
Đề bài Vận dụng trang 55 SGK Toán 10 tập 1 – Chân trời sáng tạo Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được xem là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên) a) Vận tốc xuất phát của cầu là 12 m/s b) Vị trí phát cầu cách mặt đất 1,3 m. Lưu ý: Các thông số về sân cầu lông đơn được cho trong Hình 11.
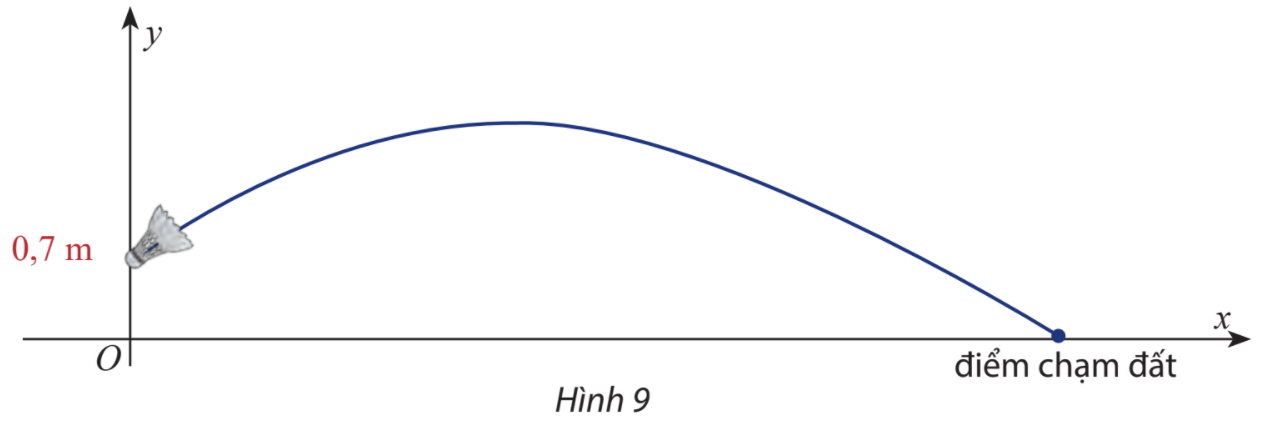
Phương pháp giải - Xem chi tiết Lần phát cầu được xem là hợp lệ nếu cầu ở trên mặt lưới (tại vị trí lưới phân cách) và điểm rơi không ra khỏi đường biên cuối sân đối phương. Lập phương trình quỹ đạo của cầu lông: \(y = \frac{{ - g{x^2}}}{{2.{v_0}^2.{{\cos }^2}\alpha }} + \tan (\alpha ).x + {y_0}\) a) Chỉ ra điểm rơi của cầu nằm ngoài đường biên ngoài bằng cách tính khoảng cách từ vị trí phát cầu đến vị trí cầu rơi b) Tìm tung độ của điểm (có hoành độ là điểm đặt lưới phân cách) với độ cao của lưới. Tính khoảng cách từ vị trí phát cầu đến vị trí cầu rơi xem cầu có thuộc khu vực được tính là hợp lệ hay không. Lời giải chi tiết a) Chọn hệ trục tọa độ như Hình 9 (vị trí rơi của cầu thuộc trục hoành và vị trí cầu rời mặt vợt thuộc trục tung).
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 12\;m/s\), phương trình quỹ đạo của cầu là: \(y = \frac{{ - 9,8}}{{{{2.12}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7\) Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \( - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = 0\) ta được \({x_1} \approx - 1,11\) và \({x_2} \approx 13,84\) Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84 m > 13,4 m (chiều dài cả sân) Vậy lần phát cầu đã bị hỏng vì điểm rơi của cầu nằm ngoài đường biên ngoài. b) Ta so sánh tung độ của điểm trên quỹ đạo (có hoành động bằng khoảng cách từ điểm phát cầu đến chân lưới phân cách) với chiều cao mép trên của lưới. Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 8\;m/s\), vị trí phát cầu cách mặt đất 1,3 m. Phương trình quỹ đạo của cầu là: \(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\) Khi \(x = 4,\)ta có \(y = - \frac{{4,9}}{{48}}{.4^2} + \frac{{\sqrt 3 }}{3}.4 + 1,3 \approx 1,98 > 1,524\) Vậy quỹ đạo của cầu cao hơn mép trên của lưới. Tiếp theo ta kiểm tra vị trí cầu rơi có vượt đường biên ngoài hoặc chưa tới đường biên trong hay không. Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\) ta được \({x_1} \approx - 1,73\) và \({x_2} \approx 7,38\) Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 7.38 m.
Dễ thấy: độ dài h (chiều dài của khu vực hợp lệ) là: \(13,4:2 - 1,98 -0,76= 3,96\) (m). Do đó lần phát là hợp lệ nếu khoảng cách từ vị trí phát đến điểm rơi thuộc khoảng \(4 + 1,98 = 5,98(m)\) và \(4 + 1,98 +3,96= 9,94(m)\) và \(5,98 < 7,38 < 9,94\). Như vậy vị trí quả cầu trên mặt đất nằm giữa đường biên trong và đường biên ngoài. Kết luận: lần phát cầu này được coi là hợp lệ.
|





















Danh sách bình luận