Giải bài 5 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạoCho hàm số y = 2x^2 + x + m. Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5. Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Quảng cáo
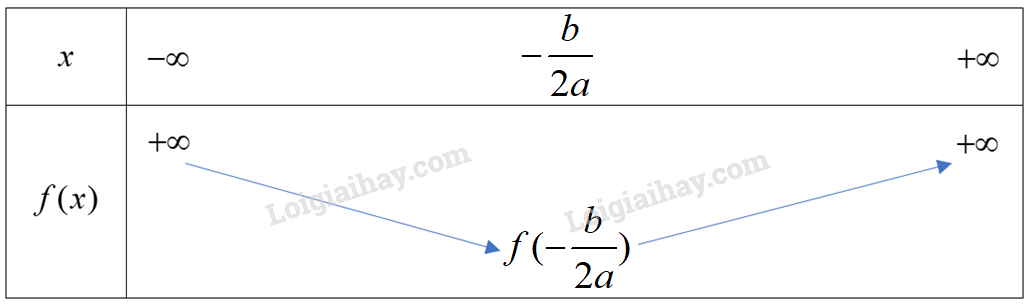
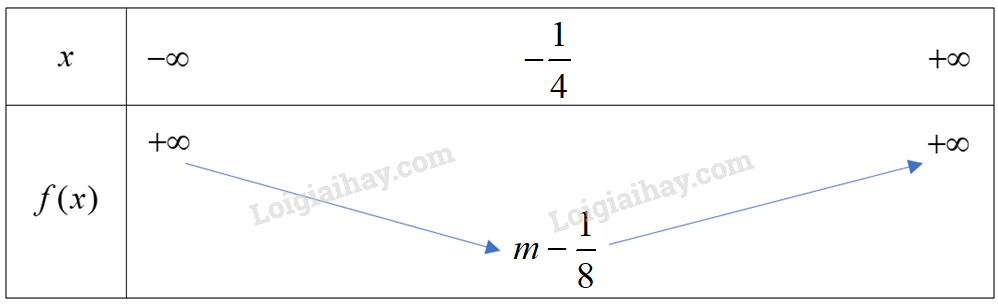
Đề bài Cho hàm số \(y = 2{x^2} + x + m\). Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5. Phương pháp giải - Xem chi tiết Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}};{y_S} = f(\frac{{ - b}}{{2a}})\) \(a = 2 > 0\) nên ta có bảng biến thiên sau: Hàm số đạt giá trị nhỏ nhất bằng \(f( - \frac{b}{{2a}})\) tại \(x = - \frac{b}{{2a}}.\) => Tìm m để \(f( - \frac{b}{{2a}}) = 5\) Lời giải chi tiết Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 1}}{{2.2}} = - \frac{1}{4};{y_S} = f( - \frac{1}{4}) = 2{\left( { - \frac{1}{4}} \right)^2} + \left( { - \frac{1}{4}} \right) + m = m - \frac{1}{8}\) Ta có: \(a = 2 > 0\), hàm số có bảng biến thiên dạng: Hàm số đạt giá trị nhỏ nhất bằng \(m - \frac{1}{8} = 5 \Leftrightarrow m = \frac{{41}}{8}.\) Vậy \(m = \frac{{41}}{8}\) thì hàm số đạt giá trị nhỏ nhất bằng 5.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
