Giải mục 3 trang 52, 53 SGK Toán 10 tập 1 - Chân trời sáng tạo

HĐ Khám phá 3

Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.

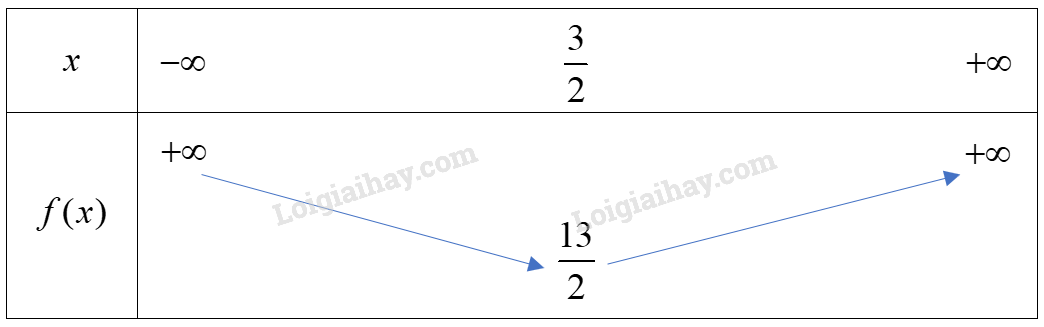
Phương pháp giải:

Quan sát đồ thị hàm số trên các khoảng $( - \infty ; - \frac{b}{{2a}})$ và $( - \frac{b}{{2a}}; + \infty )$

Trên (a’; b’): đồ thị có dạng đi lên từ trái sang phải thì hàm số đó đồng biến trên (a’;b’).

Trên (c; d): đồ thị có dạng đi xuống từ trái sang phải thì hàm số đó nghịch biến trên (c;d).

Lời giải chi tiết:

a)

Trên $( - \infty ; - \frac{b}{{2a}})$ đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên $( - \infty ; - \frac{b}{{2a}})$

Trên $( - \frac{b}{{2a}}; + \infty )$ đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên $( - \frac{b}{{2a}}; + \infty )$

Vậy hàm số có khoảng đồng biến là $( - \frac{b}{{2a}}; + \infty )$, khoảng nghịch biến là $( - \infty ; - \frac{b}{{2a}})$

b)

Trên $( - \infty ; - \frac{b}{{2a}})$ đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên $( - \infty ; - \frac{b}{{2a}})$

Trên $( - \frac{b}{{2a}}; + \infty )$ đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên $( - \frac{b}{{2a}}; + \infty )$

Vậy hàm số có khoảng đồng biến là $( - \infty ; - \frac{b}{{2a}})$, khoảng nghịch biến là $( - \frac{b}{{2a}}; + \infty )$

Thực hành 3

Tìm khoảng đồng biến, khoảng nghịch biến của hàm số $y = 2{x^2} - 6x + 11.$ Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?

Phương pháp giải:

Lập bảng biến thiên, xác định khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số.

Lời giải chi tiết:

Đỉnh S có tọa độ: ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 6)}}{{2.2}} = \frac{3}{2};{y_S} = 2.{\left( {\frac{3}{2}} \right)^2} - 6.\frac{3}{2} + 11 = \frac{{13}}{2}.$

Hay $S\left( {\frac{3}{2};\frac{{13}}{2}} \right).$

Vì hàm số bậc hai có $a = 2 > 0$ nên ta có bảng biến thiên sau:

Hàm số đồng biến trên khoảng $(\frac{3}{2}; + \infty )$ và nghịch biến trên khoảng $( - \infty ;\frac{3}{2})$

Hàm số đạt giá trị nhỏ nhất bằng $\frac{{13}}{2}$ khi $x = \frac{3}{2}$

Do đó hàm số không thể đạt giá trị bằng -1 vì $- 1 < \frac{{13}}{2}.$