Giải mục 2 trang 90, 91 SGK Toán 10 tập 1 - Chân trời sáng tạo

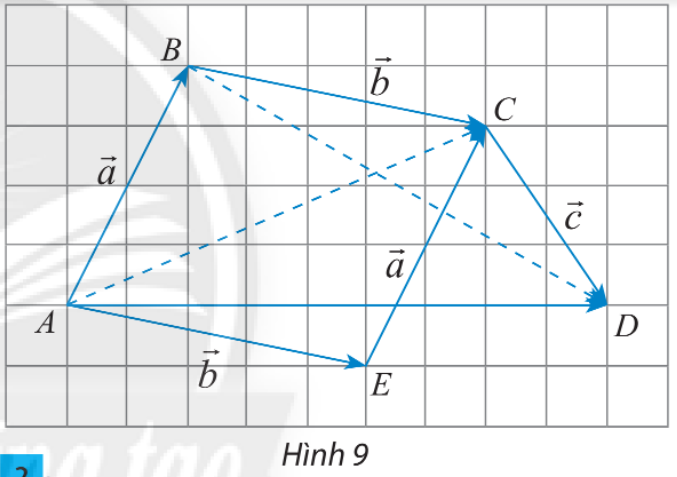
HĐ Khám phá 2

Cho 3 vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được:

a) $\overrightarrow a  + \overrightarrow b  = \overrightarrow {AB}  + \overrightarrow {BC}  = ?$

$\overrightarrow b  + \overrightarrow a  = \overrightarrow {AE}  + \overrightarrow {EC}  = ?$

b) $\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \left( {\overrightarrow {AB}  + \overrightarrow {BC} } \right) + \overrightarrow {CD}  = \overrightarrow {AC}  + \overrightarrow {CD}  = ?$

$\overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right) = \overrightarrow {AB}  + \left( {\overrightarrow {BC}  + \overrightarrow {CD} } \right) = \overrightarrow {AB}  + \overrightarrow {BD}  = ?$

Phương pháp giải:

Bước 1: Áp dụng quy tắc 3 điểm: $\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC}$;

Bước 2: So sánh các vectơ vừa tìm được

Lời giải chi tiết:

a)       Áp dụng quy tắc ba điểm ta có:

$\overrightarrow a  + \overrightarrow b  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC}$;

$\overrightarrow b  + \overrightarrow a  = \overrightarrow {AE}  + \overrightarrow {EC}  = \overrightarrow {AC}$

$\Rightarrow \overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a$

b)       Áp dụng quy tắc ba điểm ta có:

$\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \left( {\overrightarrow {AB}  + \overrightarrow {BC} } \right) + \overrightarrow {CD}  = \overrightarrow {AC}  + \overrightarrow {CD}  = \overrightarrow {AD}$

$\overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right) = \overrightarrow {AB}  + \left( {\overrightarrow {BC}  + \overrightarrow {CD} } \right) = \overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {AD}$

$\Rightarrow \left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)$

Thực hành 3

Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:

a)       $\overrightarrow a  = \left( {\overrightarrow {AC}  + \overrightarrow {BD} } \right) + \overrightarrow {CB} ;$                       

b) $\overrightarrow a  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {BC}  + \overrightarrow {DA} .$ 

Phương pháp giải:

Bước 1: Sử dụng tính chất giao hoán, kết hợp, cộng với vectơ $\overrightarrow 0$ tìm tổng các vectơ

Bước 2: Tính độ dài vectơ vừa tìm đc, độ dài vectơ $\overrightarrow {AB}$ là \(\left| 

Lời giải chi tiết:

a)       $\begin{array}{l}\overrightarrow a  = \left( {\overrightarrow {AC}  + \overrightarrow {BD} } \right) + \overrightarrow {CB}  = \left( {\overrightarrow {AC}  + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {AD}\\  \Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}$

b)       $\begin{array}{l}\overrightarrow a  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {BC}  + \overrightarrow {DA}  = \left( {\overrightarrow {AB}  + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD}  + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC}  + \overrightarrow {AA}  = \overrightarrow {AC}  + \overrightarrow 0  = \overrightarrow {AC} \end{array}$

$AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{1^2} + {1^2}}  = \sqrt 2$

$\Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AC} } \right| = \sqrt 2$