Giải bài 3 trang 93 SGK Toán 10 tập 1 – Chân trời sáng tạo

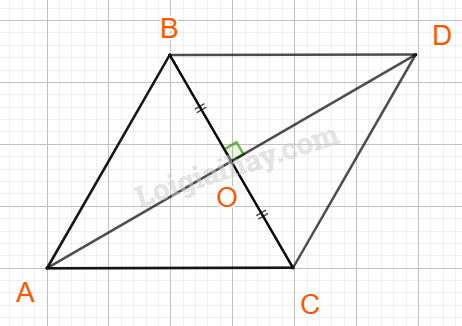
Đề bài

Cho tam giác đều ABC cạnh bằng a. Tính độ dài các vectơ:

a) \(\overrightarrow {BA}  + \overrightarrow {AC} \);               

b) \(\overrightarrow {AB}  + \overrightarrow {AC} \);               

c) \(\overrightarrow {BA}  - \overrightarrow {BC} \).

Lời giải chi tiết

a)  \(\)\(\overrightarrow {BA}  + \overrightarrow {AC}  = \overrightarrow {BC}  \Rightarrow \left| {\overrightarrow {BC} } \right| = BC = a\)

b) Dựng hình bình hành ABDC, giao điểm của hai đường chéo là O ta có:

\(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \)

\(AD = 2AO = 2\sqrt {A{B^2} - B{O^2}}  = 2\sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = a\sqrt 3 \)

\( \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt 3 \)

c) \(\overrightarrow {BA}  - \overrightarrow {BC}  = \overrightarrow {BA}  + \overrightarrow {CB}  = \overrightarrow {CB}  + \overrightarrow {BA}  = \overrightarrow {CA} \)

\( \Rightarrow \left| {\overrightarrow {BA}  - \overrightarrow {BC} } \right| = \left| {\overrightarrow {CA} } \right| = CA = a\)