Giải mục 3 trang 91, 92 SGK Toán 10 tập 1 - Chân trời sáng tạo

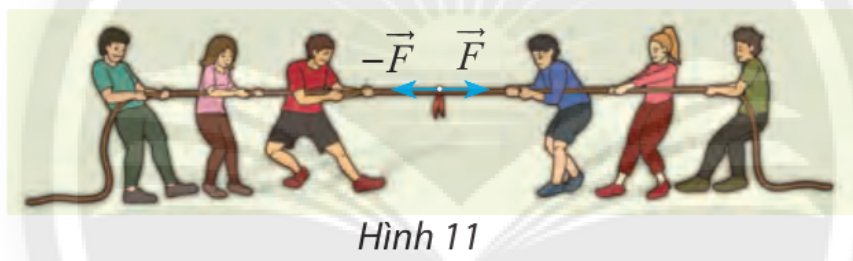
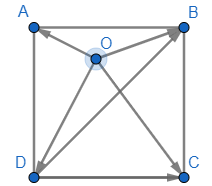
HĐ Khám phá 3

Tìm hợp lực của hai lực đối nhau \(\overrightarrow F \) và \( - \overrightarrow F \) (hình 11)

Lời giải chi tiết:

\( \overrightarrow F  + \left( { - \overrightarrow F } \right) =\overrightarrow F - \overrightarrow F = \overrightarrow 0 \) 

Thực hành 4

Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:

a) \(\overrightarrow a  = \overrightarrow {OB}  - \overrightarrow {OD} ;\)                              

b) \(\overrightarrow b  = \left( {\overrightarrow {OC}  - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB}  - \overrightarrow {DC} } \right)\).

Phương pháp giải:

Bước 1: Thay thế vectơ bằng nhau rồi tìm tổng.

Bước 2: Tìm độ dài vectơ vừa tìm đc, độ dài vectơ \(\overrightarrow {AB} \) là \(\left| {\overrightarrow {AB} } \right| = AB\). 

Lời giải chi tiết:

Ta có: \(AB = BC = CD = DA = 1;\)

            \(AC = BD = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{1^2} + {1^2}}  = \sqrt 2 \)

a) \(\overrightarrow a  = \overrightarrow {OB}  - \overrightarrow {OD}  = \overrightarrow {OB}  + \overrightarrow {DO}  = \left( {\overrightarrow {DO}  + \overrightarrow {OB} } \right) = \overrightarrow {DB} \)

\( \Rightarrow \left| {\overrightarrow a } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)

b)  \(\overrightarrow b = \left( {\overrightarrow {OC}  - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB}  - \overrightarrow {DC} } \right)\)

   \( = \left( {\overrightarrow {OC}  + \overrightarrow {AO} } \right) + \left( {\overrightarrow {DB}  + \overrightarrow {CD} } \right) = \left( {\overrightarrow {AO}  + \overrightarrow {OC} } \right) + \left( {\overrightarrow {CD}  + \overrightarrow {DB} } \right)\)

   \( = \overrightarrow {AC}  + \overrightarrow {CB}  = \overrightarrow {AB} \)

\( \Rightarrow \left| {\overrightarrow b } \right| = \left| {\overrightarrow {AB} } \right| = AB = 1\)

Chú ý khi giải:

Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại