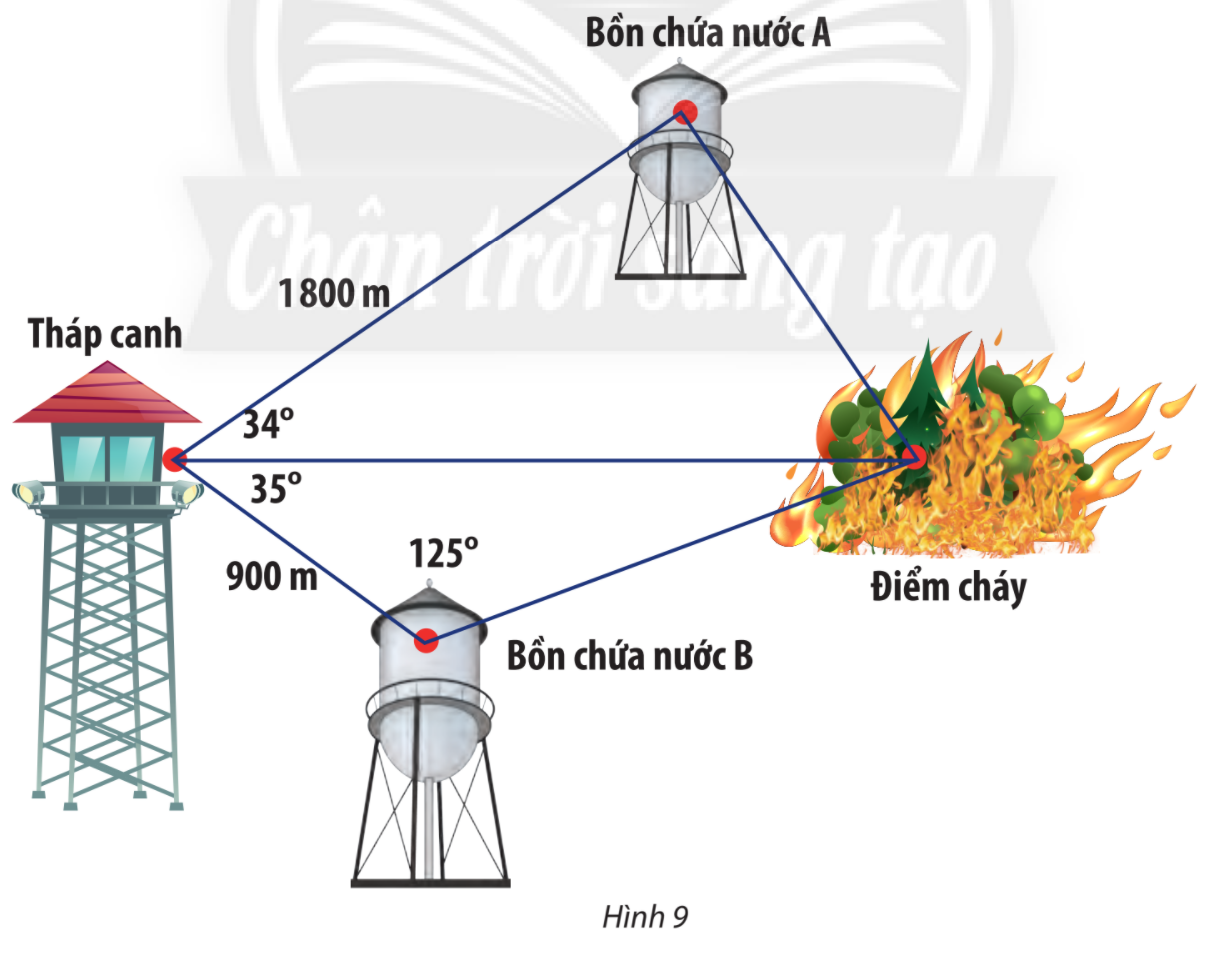
Giải mục 2 trang 67, 68, 69 SGK Toán 10 tập 1 - Chân trời sáng tạoTrong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
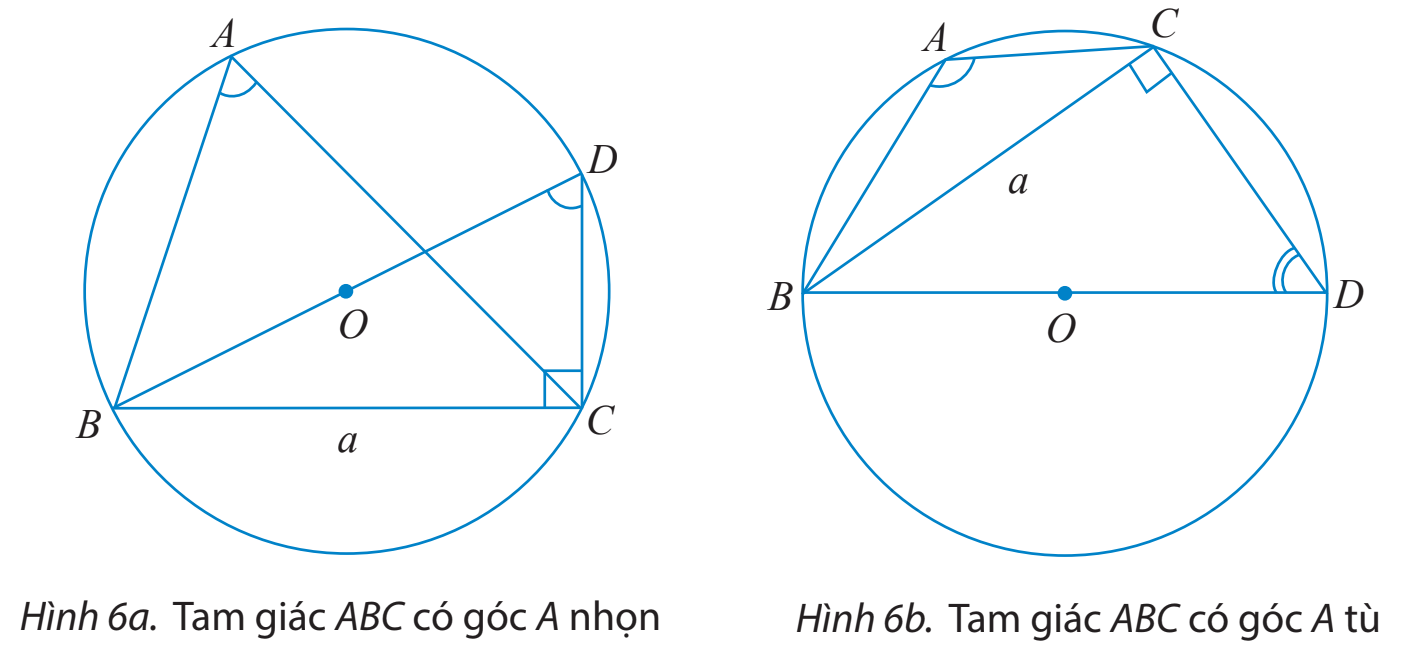
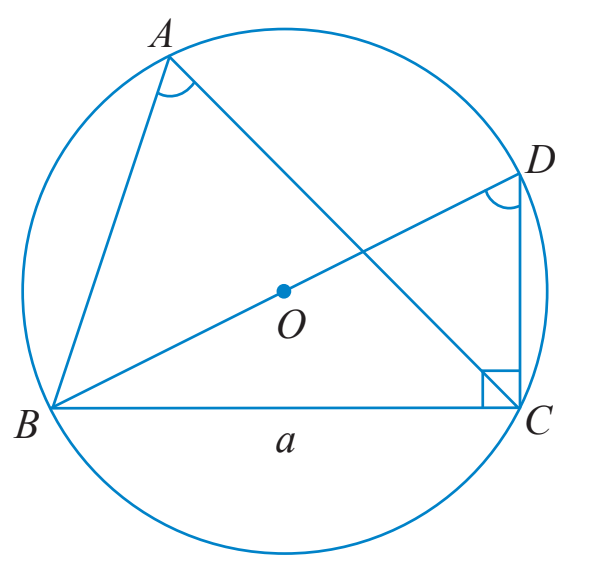
HĐ Khám phá 2 a) Cho tam giác ABC không phải là tam giác vuông có \(BC = a,AC = b,AB = c\) và R là bán kính của đường trong ngoại tiếp tam giác đó. Vẽ đường kính BD. i) Tính \(\sin \widehat {BDC}\) theo a và R. ii) Tìm mối liên hệ giữa hai góc \(\widehat {BAC}\) và \(\widehat {BDC}\). Từ đó chứng minh rằng \(2R = \frac{a}{{\sin A}}.\)
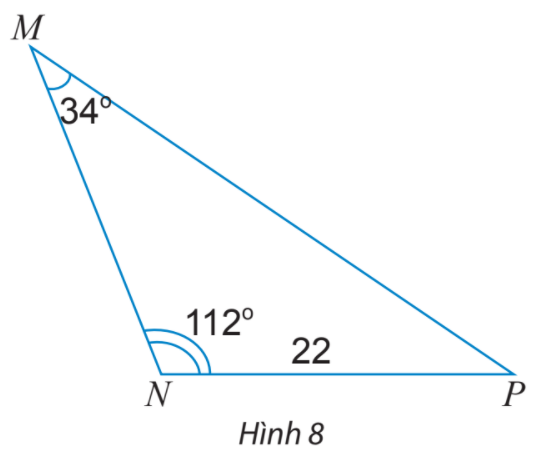
b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức \(2R = \frac{a}{{\sin A}}.\) Lời giải chi tiết: a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\) b) TH1: Tam giác ABC có góc A nhọn \(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC. \( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\) TH2: Tam giác ABC có góc A tù \(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O). \( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\) Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\) b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O). Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\) Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\) Thực hành 2 Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.
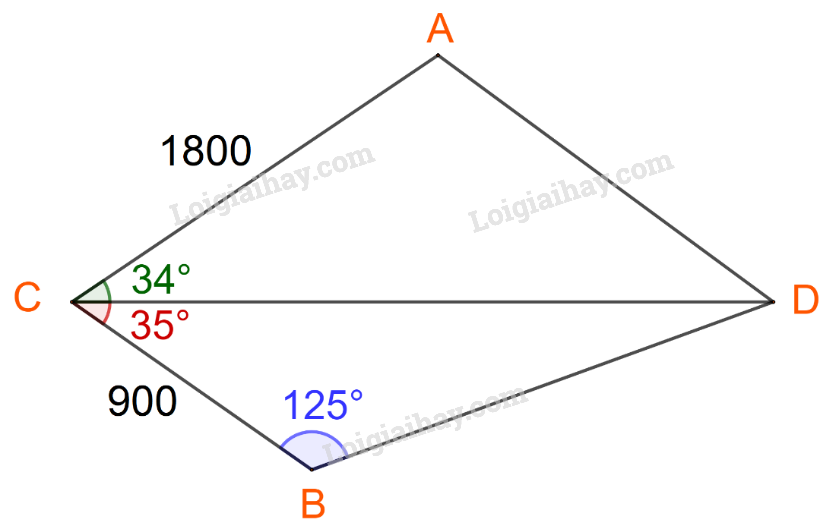
Phương pháp giải: Áp dụng định lí sin cho tam giác MNP: \(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}}\) Lời giải chi tiết: Ta có: \(NP = 22,\;\widehat P = {180^o} - ({112^o} + {34^o}) = {34^o}\) Áp dụng định lí sin, ta có: \(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}}\) Suy ra: \(MP = \frac{{NP.\sin N}}{{\sin M}} = \frac{{22.\sin {{112}^o}}}{{\sin {{34}^o}}} \approx 36,48\) \(MN = \frac{{NP.\sin P}}{{\sin M}} = \frac{{22.\sin {{34}^o}}}{{\sin {{34}^o}}} = 22.\) Vận dụng 2 Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn?
Phương pháp giải: Áp dụng định lí sin, tính khoảng cách từ bồn chứa nước A đến đám cháy. Áp dụng định lí cosin, tính khoảng cách từ bồn chứa nước B đến đám cháy. Lời giải chi tiết: Đặt các điểm A, B, C, D lần lượt là vị trí bồn chứa nước A, bồn chứa nước B, tháp canh và đám cháy. Ta có: \(CB = 900,\;\widehat {CDB} = {180^o} - ({125^o} + {35^o}) = {20^o}\) Áp dụng định lí sin trong tam giác CBD, ta có: \(\frac{{CB}}{{\sin D}} = \frac{{BD}}{{\sin C}} = \frac{{CD}}{{\sin B}}\) Suy ra: \(BD = \frac{{CB.\sin C}}{{\sin D}} = \frac{{900.\sin {{35}^o}}}{{\sin {{20}^o}}} \approx 1509,3\) \(CD = \frac{{CB.\sin B}}{{\sin D}} = \frac{{900.\sin {{125}^o}}}{{\sin {{20}^o}}} = 2155,5\) Áp dụng định lí cosin trong tam giác ACD ta có: \(\begin{array}{l}A{D^2} = A{C^2} + C{D^2} - 2.AC.CD.\cos \widehat {ACD}\\ \Leftrightarrow A{D^2} = {1800^2} + 2155,{5^2} - 2.1800.2155,5.\cos {34^o} \approx 1453014,5\\ \Leftrightarrow AD \approx 1205,4\end{array}\) Vì \(AD < BD\) nên khoảng cách từ bồn chứa nước A đến đám cháy là ngắn hơn. Vậy nên dẫn nước từ bồn chứa nước A để dập tắt đám cháy nhanh hơn.
|





















Danh sách bình luận