Giải bài 4 trang 73 SGK Toán 10 tập 1 – Chân trời sáng tạo

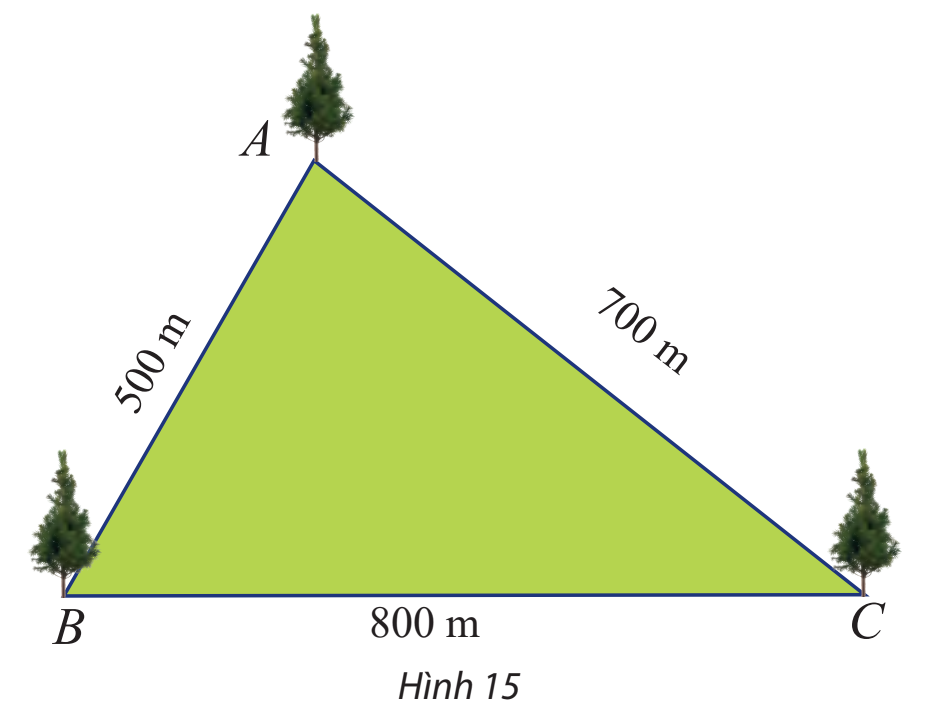
Đề bài

Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.

Lời giải chi tiết

Đặt \(a = BC,b = AC,c = AB\)

Ta có: \(a = 800,b = 700,c = 500.\)

Áp dụng định lí cosin, ta có:

\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}.\)

Suy ra:

\(\begin{array}{l}\cos A = \frac{{{{700}^2} + {{500}^2} - {{800}^2}}}{{2.700.500}} = \frac{1}{7} \Rightarrow \widehat A = {81^o}47'12,44'';\\\cos B = \frac{{{{500}^2} + {{800}^2} - {{700}^2}}}{{2.500.800}} = \frac{1}{2} \Rightarrow \widehat B = {60^o};\\\cos C = \frac{{{{800}^2} + {{700}^2} - {{500}^2}}}{{2.800.700}} = \frac{{11}}{{14}} \Rightarrow \widehat C = {38^o}12'47,56''.\end{array}\)

Vậy \(\widehat A = {81^o}47'12,44'';\widehat B = {60^o};\widehat C = {38^o}12'47,56''.\)