Giải bài 6 trang 73 SGK Toán 10 tập 1 – Chân trời sáng tạo

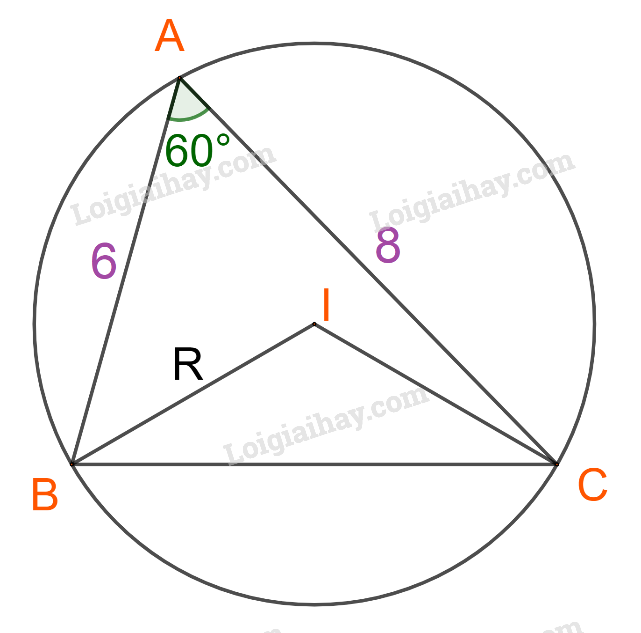
Đề bài

Cho tam giác ABC có AB = 6, AC = 8 và \(\widehat A = {60^o}\).

a) Tính diện tích tam giác ABC.

b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.

Lời giải chi tiết

Đặt a = BC, b = AC, c = AB.

a) Áp dụng công thức \(S = \frac{1}{2}bc\sin A\), ta có:

\({S_{ABC}} = \frac{1}{2}.8.6.\sin {60^o} = \frac{1}{2}.8.6.\frac{{\sqrt 3 }}{2} = 12\sqrt 3 \).

b) Áp dụng định lí cosin cho tam giác ABC ta được:

\(B{C^2} = {a^2} = {8^2} + {6^2} - 2.8.6.\cos {60^o} = 52\)

\(\Rightarrow BC = 2\sqrt {13}\).

Xét tam giác IBC ta có:

Góc \(\widehat {BIC} = 2.\widehat {BAC} = {120^o}\)(góc ở tâm và góc nội tiếp cùng chắn một cung).

\(IB = IC = R = \frac{a}{{2\sin A}} = \frac{{2\sqrt {13} }}{{2.\frac{{\sqrt 3 }}{2}}} = \frac{{2\sqrt {39} }}{3}\).

\( \Rightarrow {S_{IBC}} = \frac{1}{2}.\frac{{2\sqrt {39} }}{3}.\frac{{2\sqrt {39} }}{3}\sin {120^o} = \frac{{13\sqrt 3 }}{3}\).