Giải mục 1 trang 88, 89, 90 SGK Toán 10 tập 1 - Chân trời sáng tạo

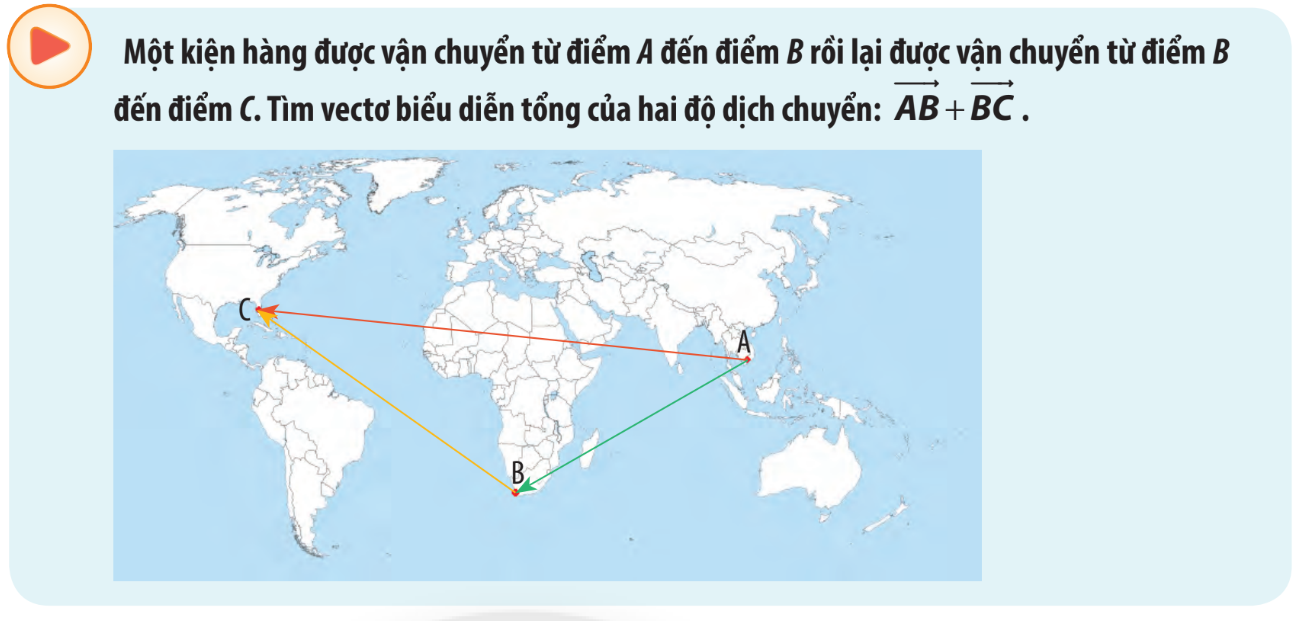
HĐ Khởi động

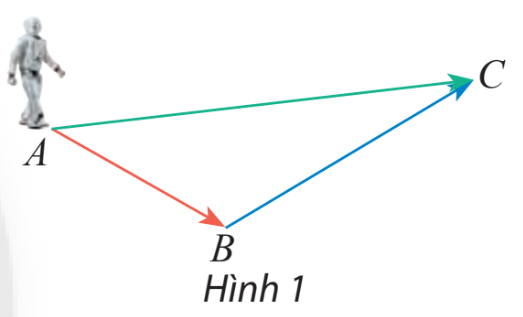
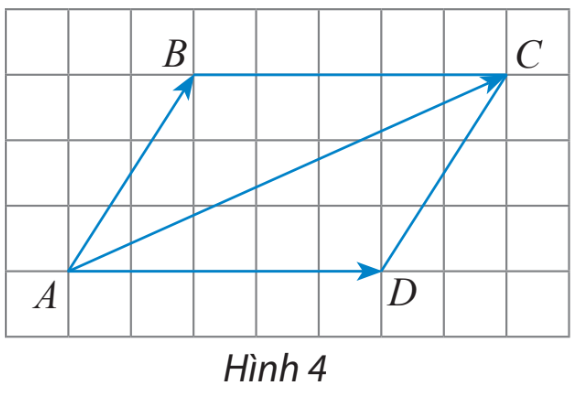
Lời giải chi tiết:

\(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

HĐ Khám phá 1

Một robot thực hiện liên tiếp hai chuyển động có độ dịch chuyển lần lượt được biểu diễn bởi 2 vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) (Hình 1). Tìm vectơ biểu diễn sự dịch chuyển của rô bốt sau hai sự dịch chuyển trên.

Phương pháp giải:

Xác định A là điểm đầu và C là điểm cuối, dùng đoạn thẳng có hướng nối 2 điểm trên.

Lời giải chi tiết:

Ta thấy rô bốt đi từ A đến B, sau đó đi từ B đến C, vậy cả 2 lần di chuyển thì ta thấy điểm cuất phát là A và điểm kết thúc là C.

Suy ra vectơ biểu diễn sự dịch chuyển của rô bốt sau hai lần dịch chuyển là vectơ \(\overrightarrow {AC} \)

HĐ Khám phá 2

Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \)

Phương pháp giải:

Tìm vectơ bằng với vectơ \(\overrightarrow {AD} \), sau đó áp dụng quy tắc ba điểm  

Lời giải chi tiết:

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD}  = \overrightarrow {BC} \)\(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \) (đpcm)

Thực hành 1

Cho hình thang ABCD có đáy là AB và CD. Cho biết \(\overrightarrow a  = \overrightarrow {AC}  + \overrightarrow {CB} ;\overrightarrow b  = \overrightarrow {DB}  + \overrightarrow {BC} \). Chứng minh rằng hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.

Phương pháp giải:

Bước 1: Áp dụng quy tắc ba điểm, tìm vectơ \(\overrightarrow a \) và \(\overrightarrow b \)

Bước 2: Xác định hướng của vectơ vừa tìm được

Bước 3: So sánh hướng của 2 vectơ

Lời giải chi tiết:

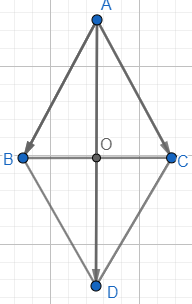
Áp dụng quy tắc ba điểm ta có:

\(\overrightarrow a  = \overrightarrow {AC}  + \overrightarrow {CB}  = \overrightarrow {AB} \); \(\overrightarrow b  = \overrightarrow {DB}  + \overrightarrow {BC}  = \overrightarrow {DC} \)

Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng

Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.

Thực hành 2

Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB}  + \overrightarrow {AC}\) 

Phương pháp giải:

Bước 1: Dựng hình bình hành ABDC

Bước 2: Áp dụng quy tắc hình bình hành tìm tổng vectơ \(\overrightarrow {AB}  + \overrightarrow {AC} \)

Bước 3: Tìm độ dài vectơ tổng.

Lời giải chi tiết:

Dựng hình bình hành ABDC.

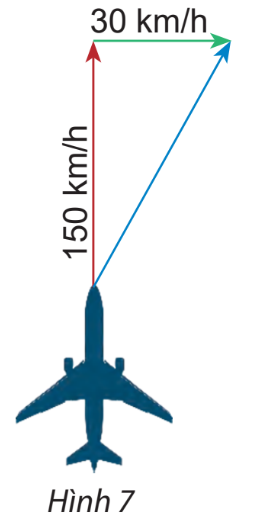
Áp dụng quy tắc hình bình hành vào ABDC ta có:

\(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD}  \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)

Gọi O là giao điểm của AD và BC, ta có:

\(AO = \sqrt {A{B^2} - B{O^2}}  = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}}  = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt 3 }}{2}\)

\(AD = 2AO = a\sqrt 3  \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = a\sqrt 3 \)

Vậy độ dài vectơ \(\overrightarrow {AB}  + \overrightarrow {AC} \) là \(a\sqrt 3 \)

Vận dụng 1

Một máy bay có vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên.

Phương pháp giải:

Bước 1: Áp dụng quy tắc 3 điểm để tìm vectơ tổng

Bước 2: Tìm độ dài vectơ tổng vừa tìm được. 

Lời giải chi tiết:

Gọi vectơ chỉ vận tốc của máy bay là vectơ \(\overrightarrow {AB} \) và vectơ chỉ vận tốc của gió là vectơ \(\overrightarrow {BC} \).

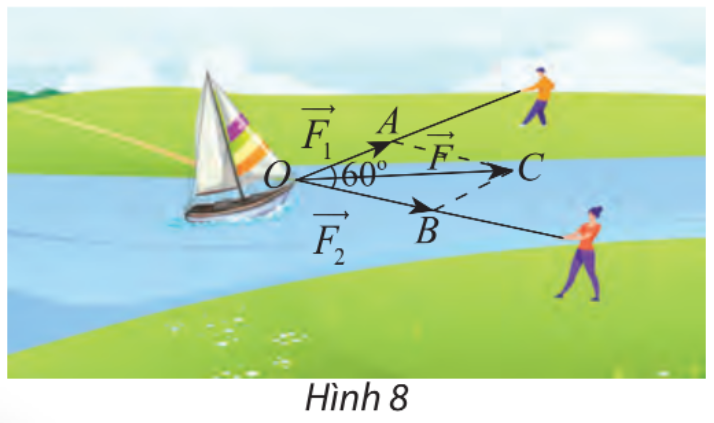
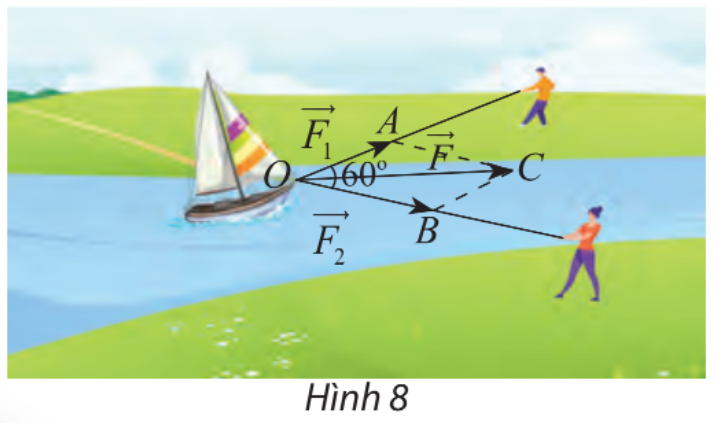
Ta có: \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Áp dụng định lý Pitago ta có:

\(AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{{150}^2} + {{30}^2}}  = 30\sqrt {26} \)   

Vậy độ dài vectơ tổng của hai vectơ nói trên là \(30\sqrt {26} \) km/h

Vận dụng 2

Hai người cùng kéo một con thuyền với hai lực \(\overrightarrow {{F_1}}  = \overrightarrow {OA} ,\overrightarrow {{F_2}}  = \overrightarrow {OB} \) có độ lớn lần lượt là 400 N, 600 N (hình 8). Cho biết góc giữa hai vectơ là \({60^\circ }\). Tìm độ lớn của vectơ hợp lực \(\overrightarrow F \) là tổng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \)

Phương pháp giải:

Bước 1: Dựng hình bình hành AOBC

Bước 2: Áp dụng quy tắc hình bình hành tìm tổng lực

Bước 3: Xác định độ lớn của vectơ tổng.

Lời giải chi tiết:

Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  = \overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OC} \);

\(AC = OB = 600\); \(\widehat {AOB} = 60^\circ  \Rightarrow \widehat {OAC} = 120^\circ \) (hai góc bù nhau trong hình bình hành).

Áp dụng định lý cos ta có:

\(OC = \sqrt {O{A^2} + A{C^2} - 2OA.AC.\cos (120^\circ )} \)

            \( = \sqrt {{{400}^2} + {{600}^2} - 2.400.600.\cos (120^\circ )}  \simeq 871,78\)N

Vậy độ lớn của vectơ hợp lực \(\overrightarrow F \) gần bằng 871,78 N