Giải mục 1 trang 6, 7 SGK Toán 10 tập 2 - Chân trời sáng tạo

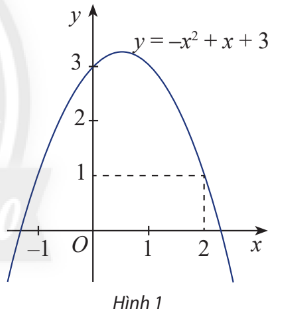
HĐ Khám phá 1

Đồ thị của hàm số $y = f\left( x \right) =  - {x^2} + x + 3$được biểu diễn trong hình 1

a) Biểu thức $f\left( x \right)$ là đa thức bậc mấy?

b) Xác định dấu của $f\left( 2 \right)$

Phương pháp giải:

a) Xác định số mũ cao nhất

b) Thay $x = 2$ vào $f\left( x \right)$, so sánh với 0.

Lời giải chi tiết:

a) Số mũ cao nhất của hàm số là 2, suy ra biểu thức$f\left( x \right)$đã cho là đa thức bậc hai

b) Thay $x = 2$ vào $f\left( x \right)$ ta có:

$f\left( 2 \right) =  - {2^2} + 2 + 3 = 1 > 0$

Suy ra $f\left( 2 \right)$ dương.

Thực hành 1

Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại $x = 1$.

a) $f\left( x \right) = 2{x^2} + x - 1$;

b) $g\left( x \right) =  - {x^4} + 2{x^2} + 1$

c) $h\left( x \right) =  - {x^2} + \sqrt 2 .x - 3$

Lời giải chi tiết:

a) Biểu thức $f\left( x \right) = 2{x^2} + x - 1$ là một tam thức bậc hai

          $f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0$ nên $f\left( x \right)$ dương tại $x = 1$

b) Biểu thức $g\left( x \right) =  - {x^4} + 2{x^2} + 1$ không phải là một tam thức bậc hai

c) Biểu thức $h\left( x \right) =  - {x^2} + \sqrt 2 .x - 3$ là một tam thức bậc hai

          $h\left( 1 \right) =  - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2  - 4 < 0$ nên $h\left( x \right)$ âm tại $x = 1$

Thực hành 2

Tìm biệt thức và nghiệm của các tam thức bậc hai sau:

a) $f\left( x \right) = 2{x^2} - 5x + 2$

b) $g\left( x \right) =  - {x^2} + 6x - 9$

c) $h\left( x \right) = 4{x^2} - 4x + 9$

Phương pháp giải:

Bước 1: Xác định biệt thức $\Delta  = {b^2} - 4ac$

Bước 2: Xét dấu của $\Delta$

Bước 3: Tìm nghiệm

+) Nếu $\Delta  > 0 \Rightarrow {x_1} = \frac{{ - b + \sqrt \Delta  }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta  }}{{2a}}$

+) Nếu $\Delta  = 0 \Rightarrow {x_1} = {x_2} = \frac{{ - b}}{{2a}}$

+) Nếu $\Delta  = 0$thì tam thức bậc hai vô nghiệm

Lời giải chi tiết:

a) Tam thức bậc hai $f\left( x \right) = 2{x^2} - 5x + 2$ có $\Delta  = {\left( { - 5} \right)^2} - 4.2.2 = 9$

$\Delta  > 0$, do đó $f\left( x \right)$ có hai nghiệm phân biệt là

          ${x_1} = \frac{{5 + \sqrt 9 }}{4} = 2$ và ${x_1} = \frac{{5 - \sqrt 9 }}{4} = \frac{1}{2}$

b) Tam thức bậc hai $g\left( x \right) =  - {x^2} + 6x - 9$ có $\Delta  = {6^2} - 4.\left( { - 1} \right).\left( { - 9} \right) = 0$

$\Delta  = 0$, do đó $g\left( x \right)$có nghiệm kép ${x_1} = {x_2} = \frac{{ - 6}}{{2.\left( { - 1} \right)}} = 3$

c) Tam thức bậc hai $h\left( x \right) = 4{x^2} - 4x + 9$ có $\Delta  = {\left( { - 4} \right)^2} - 4.4.9 =  - 128$

$\Delta  < 0$, do đó $h\left( x \right)$ vô nghiệm