Giải bài 8 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạovới đơn vị tính bằng nghìn đồng. Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng nào? Quảng cáo
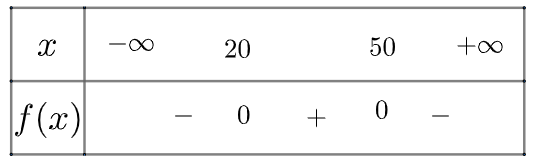
Đề bài Lợi nhuận một tháng \(p\left( x \right)\) của một quán ăn phụ thuộc vào giá trung bình x của các món ăn theo công thức \(p\left( x \right) = - 30{x^2} + 2100x - 15000\), với đơn vị tính bằng nghìn đồng. Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng nào? Phương pháp giải - Xem chi tiết Bước 1: Từ giả thiết lập bất phương trình Bước 2: Giải bất phương trình vừa tìm được Lời giải chi tiết 15 triệu đồng = 15000 nghìn đồng Từ giả thiết bài toán ta có bất phương trình \(p\left( x \right) \ge 15000 \Leftrightarrow - 30{x^2} + 2100x - 15000 \ge 15000\) \( \Rightarrow - 30{x^2} + 2100x - 30000 \ge 0\) Xét tam thức \(f\left( x \right) = - 30{x^2} + 2100x - 30000\) có \(\Delta = 810000 > 0\), có hai nghiệm phân biệt là \({x_1} = 20,{x_2} = 50\) và \(a = - 30 < 0\) Ta có bảng xét dấu như sau
Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng 20 đến 50 nghìn đồng.
|




















Danh sách bình luận