Giải bài 6 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo

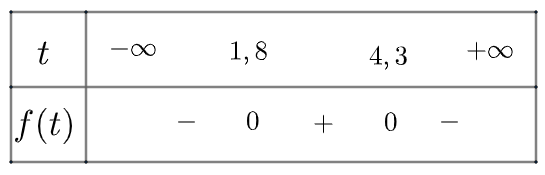
Đề bài

Một quả bóng được bắn thẳng lên từ độ cao 2 m với vận tốc ban đầu là 30 m/s. Khoảng cách quả bóng so với mặt đất t giây được cho bởi hàm số:

\(h\left( t \right) =  - 4,9{t^2} + 30t + 2\)

với \(h\left( t \right)\) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên 40 m trong thời gian bao lâu? Làm tròn kết quả đến hàng phần mười.

Lời giải chi tiết

Theo giả thiết, khoảng thời gian bóng nằm ở độ cao 40 m là nghiệm của bất phương trình sau:

\(\begin{array}{l}h\left( t \right) > 40 \Leftrightarrow  - 4,9{t^2} + 30t + 2 > 40\\ \Leftrightarrow  - 4,9{t^2} + 30t - 38 > 0\end{array}\)

Xét tam thức \(f\left( t \right) =  - 4,9{t^2} + 30t - 38\) có \(\Delta  = 155,2 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,8;{x_2} \simeq 4,3\) và có \(a =  - 4,9 < 0\)

Ta có bảng xét dấu như sau:

Từ đó cho thấy khoảng từ 1,8 s đến 4,3 s lag khoảng thời gian bóng cao so với mặt đất lớn hơn 40 m

Vậy quả bóng nằm ở độ cao trên 40 m trong thời gian 2,5 giây.