Toán 10, giải toán lớp 10 chân trời sáng tạo

Giải bài 5 trang 10 SGK Toán 10 tập 2 – Chân trời sáng tạo

Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng bằng hàm số

Quảng cáo

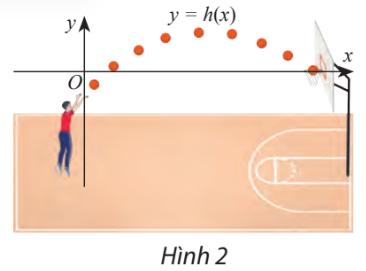
Đề bài

Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng bằng hàm số \(h\left( x \right) = - 0,1{x^2} + x - 1\). Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ và ngang vành rổ? Làm tròn các kết quả đến hàng phần mười.

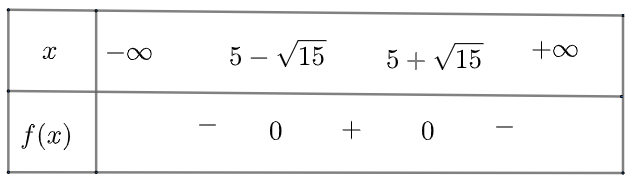
Phương pháp giải - Xem chi tiết

Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} - 4ac\)

Bước 2: Xác định nghiệm của \(h\left( x \right)\) (nếu có) \(x = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\)

Bước 3: Lập bảng xét dấu

Bước 4: Dựa vào bảng xét dấu đưa ra các khoảng theo yêu cầu

+) Khoảng mà \(h\left( x \right) > 0\) là khoảng bóng nằm cao hơn vành rổ

+) Khoảng mà \(h\left( x \right) < 0\) là khoảng bóng nằm thấp hơn vành rổ

+) Khoảng mà \(h\left( x \right) = 0\) là khoảng bóng nằm ngang vành rổ

Lời giải chi tiết

\(h\left( x \right) = - 0,1{x^2} + x - 1\) có \(\Delta = \frac{3}{5} > 0\), có hai nghiệm phân biệt là \({x_1} = 5 - \sqrt {15} ;{x_2} = 5 + \sqrt {15} \)

Ta có bảng xét dấu như sau

Vậy khoảng bóng nằm trên vành rổ là \(x \in \left( {1,2;8,9} \right)\)mét
khoảng bóng nằm dưới vành rổ là \(x \in \left( { - \infty ;1,2} \right) \cup \left( {8,9; + \infty } \right)\) mét
khoảng bóng nằm ngang vành rổ là \(x \simeq \left\{ {1,2;8,9} \right\}\)