Giải bài 2 trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạoCho AB và CD là hai dây cung vuông góc tại E của đường tròn (O) .Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ mặt phẳng để chứng minh EF vuông góc với DB Quảng cáo
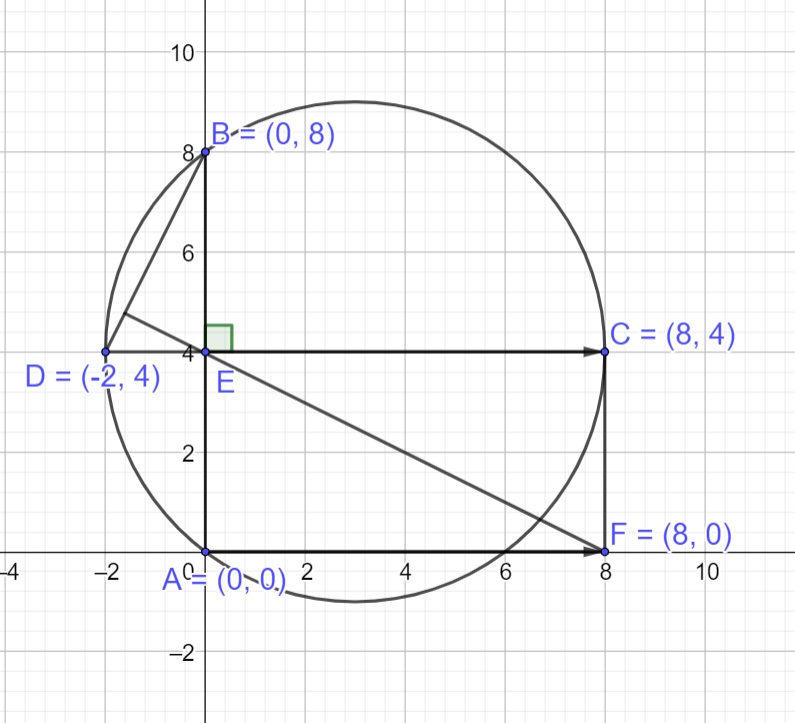
Đề bài Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O) .Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ mặt phẳng để chứng minh EF vuông góc với DB Phương pháp giải - Xem chi tiết Bước 1: Xét với đường tròn bất kì, cho tọa độ các điểm A, B, C, D Bước 2: Xác định tọa độ điểm E, F Bước 3: Tính \(\overrightarrow {EF} .\overrightarrow {DB} \), suy ra vuông góc Lời giải chi tiết Xét với đường tròn (O) có phương trình \((O):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\) Cho các điểm \(A(0;0),B(0;8),C(8;4),D( - 2;4)\) nằm trên đường tròn (O) và thỏa mãn AB vuông góc với CD
Phương trình đường thẳng đi qua hai điểm A, B có dạng \(x = 0\) Phương trình đường thẳng đi qua hai điểm C, D có dạng \(y = 4\) Ta có AB vuông góc với CD tại điểm E nên tọa độ điểm E là nghiệm của hệ sau: \(\left\{ \begin{array}{l}x = 0\\y = 4\end{array} \right. \Leftrightarrow E(0;4)\) Gọi tọa độ của điểm F là: \(F(x;y)\) ACEF là hình chữ nhật nên \(\overrightarrow {AF} = \overrightarrow {EC} \), mặt khác ta có: \(\overrightarrow {AF} = (x;y),\overrightarrow {EC} = \left( {8;0} \right)\) Suy ra tọa độ điểm F là: \(F\left( {8;0} \right)\) \(\overrightarrow {EF} = \left( {8; - 4} \right),\overrightarrow {DB} = \left( {2;4} \right) \Rightarrow \overrightarrow {EF} .\overrightarrow {BD} = 8.2 + \left( { - 4} \right).4 = 0 \Rightarrow \overrightarrow {EF} \bot \overrightarrow {BD} \) Vậy ta chứng minh được EF vuông góc với DB
|




















Danh sách bình luận