Lý thuyết Tích vô hướng của hai vecto - SGK Toán 10 CTST

1. GÓC GIỮA HAI VECTO

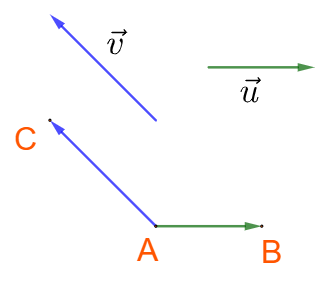
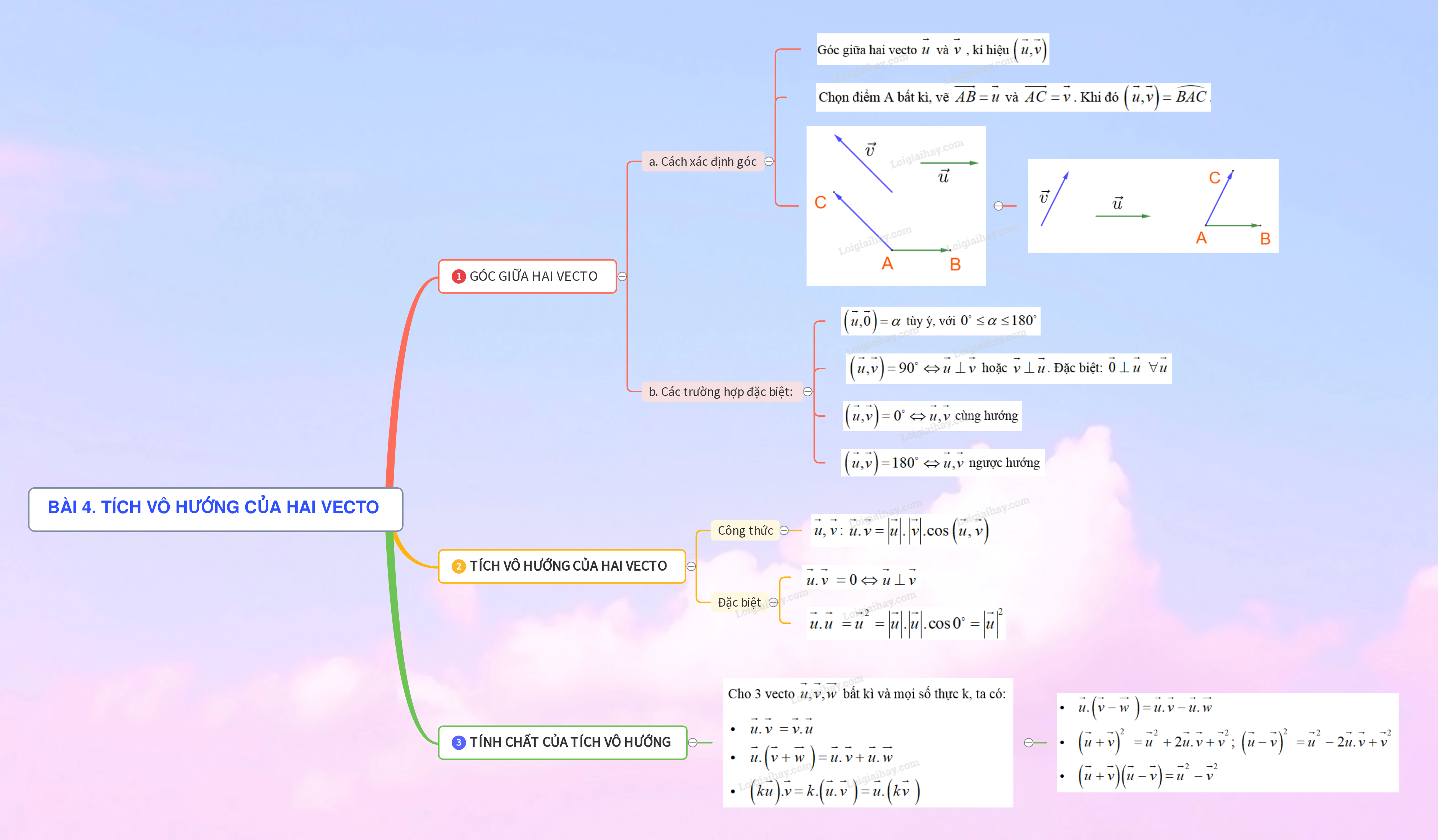
Cho hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) khác \(\overrightarrow 0 \). Góc giữa hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) , kí hiệu \(\left( {\;\overrightarrow u ,\overrightarrow v } \right)\)

a) Cách xác định góc:

Chọn điểm A bất kì, vẽ \(\overrightarrow {AB}  = \overrightarrow u \) và \(\overrightarrow {AC}  = \overrightarrow v \). Khi đó \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}\).

b) Các trường hợp đặc biệt:

+) \(\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha \) tùy ý, với \({0^ \circ } \le \alpha  \le {180^ \circ }\)

+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u  \bot \overrightarrow v \) hoặc \(\overrightarrow v  \bot \overrightarrow u \). Đặc biệt: \(\overrightarrow 0  \bot \overrightarrow u \;\;\forall \overrightarrow u \;\)

+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) cùng hướng

+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) ngược hướng

2. TÍCH VÔ HƯỚNG CỦA HAI VECTO

+) Tích vô hướng của hai vecto \(\overrightarrow u ,\;\overrightarrow v \): \(\overrightarrow u .\;\overrightarrow v  = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)

+) \(\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u  \bot \;\overrightarrow v \;\;\)

+) \(\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}\)

3. TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG

Cho 3 vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) bất kì và mọi số thực k, ta có:

\(\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v  + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v  = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}\)

Hệ quả

\(\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v  - \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; - \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u  + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u  - \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} - 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u  + \overrightarrow v } \right)\left( {\overrightarrow u  - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}\)