Giải bài 2 trang 101 SGK Toán 10 tập 1 – Chân trời sáng tạo

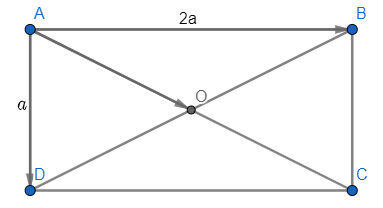
Đề bài

Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:

a) \(\overrightarrow {AB} .\overrightarrow {AO} \);

b) \(\overrightarrow {AB} .\overrightarrow {AD} \).

Lời giải chi tiết

a) \(AC = BD = \sqrt {A{B^2} + A{D^2}}  \\= \sqrt {{{\left( {2a} \right)}^2} + {a^2}}  = a\sqrt 5 \)

\(\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) = \cos \widehat {OAB} =\\ \cos \widehat {CAB} = \frac{{AB}}{{AC}} = \frac{{2a}}{{a\sqrt 5 }} = \frac{{2\sqrt 5 }}{5}\)

\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AO}  = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AO} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) \\= AB.\frac{1}{2}AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right)\\ = 2a.\frac{1}{2}.a\sqrt 5 .\frac{{2\sqrt 5 }}{5} = 2{a^2}\end{array}\)

b) \(AB \bot AD \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = 90^o  \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) =0 \Rightarrow \overrightarrow {AB} .\overrightarrow {AD}  = 0\)