Giải mục 2 trang 23, 24, 25 SGK Toán 10 tập 1 - Chân trời sáng tạoCho tập hợp E ={ x thuộc N |x < 8} ,A = { 0;1;2;3;4} ,B = { 3;4;5} Xác định các tập hợp sau đây: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
HĐ Khám phá 2 Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Hoạt động khám phá 1. a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ. b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn. Phương pháp giải: Viết tập hợp bằng cách liệt kê các phần tử. Lời giải chi tiết:
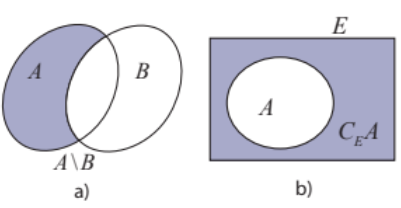
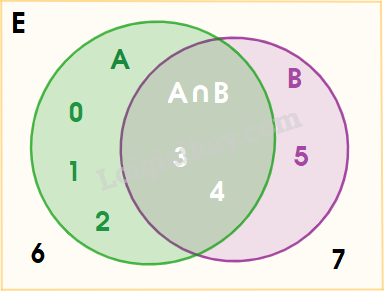
a) Tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ là: \(E = \{ {a_2};{a_7}\} \) b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn là: \(F = \{ {a_3};{a_4};{a_9}\} \) Thực hành 3 Cho tập hợp \(E = \{ x \in \mathbb{N}|x < 8\} ,A = \{ 0;1;2;3;4\} ,B = \{ 3;4;5\} \) Xác định các tập hợp sau đây: a) A\B, B\A và \((A\backslash B) \cap {\rm{(}}B\backslash A)\) b) \({C_E}(A \cap B)\) và \(({C_E}A) \cap ({C_E}B)\) c) \({C_E}(A \cup B)\) và \(({C_E}A) \cup ({C_E}B)\) Phương pháp giải:
Lời giải chi tiết: \(E = \{ x \in \mathbb{N}|x < 8\} = \{ 0;1;2;3;4;5;6;7\} \) a) Ta có: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \) b) Ta có: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \) \({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \) c) Ta có: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \) \({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)
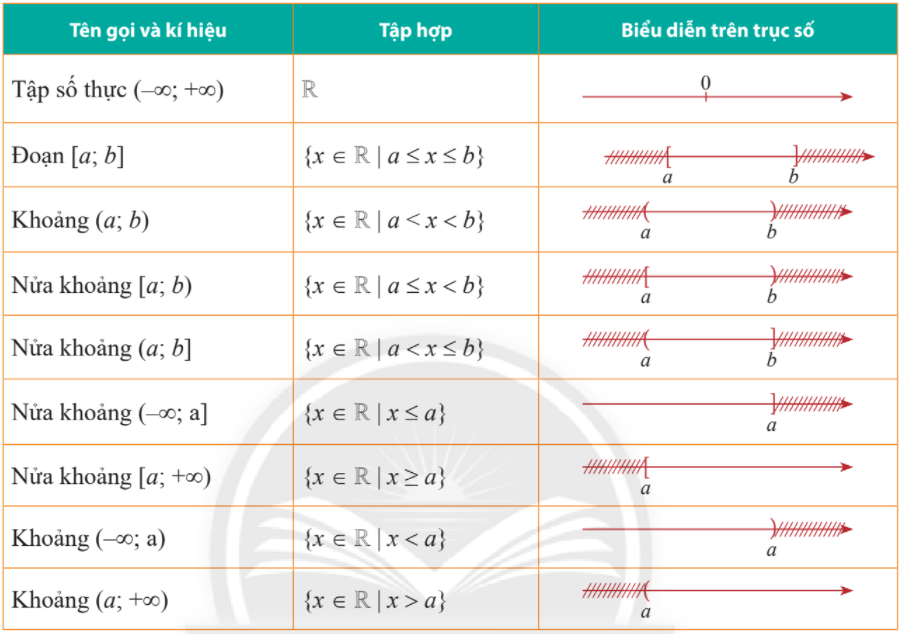
Thực hành 4 Xác định các tập hợp sau đây: a) \((1;3) \cup [ - 2;2]\) b) \(( - \infty ;1) \cap [0;\pi ]\) c) \([\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\) d) \({C_\mathbb{R}}[ - 1; + \infty )\) Phương pháp giải: Biểu diễn các tập hợp trên trục số
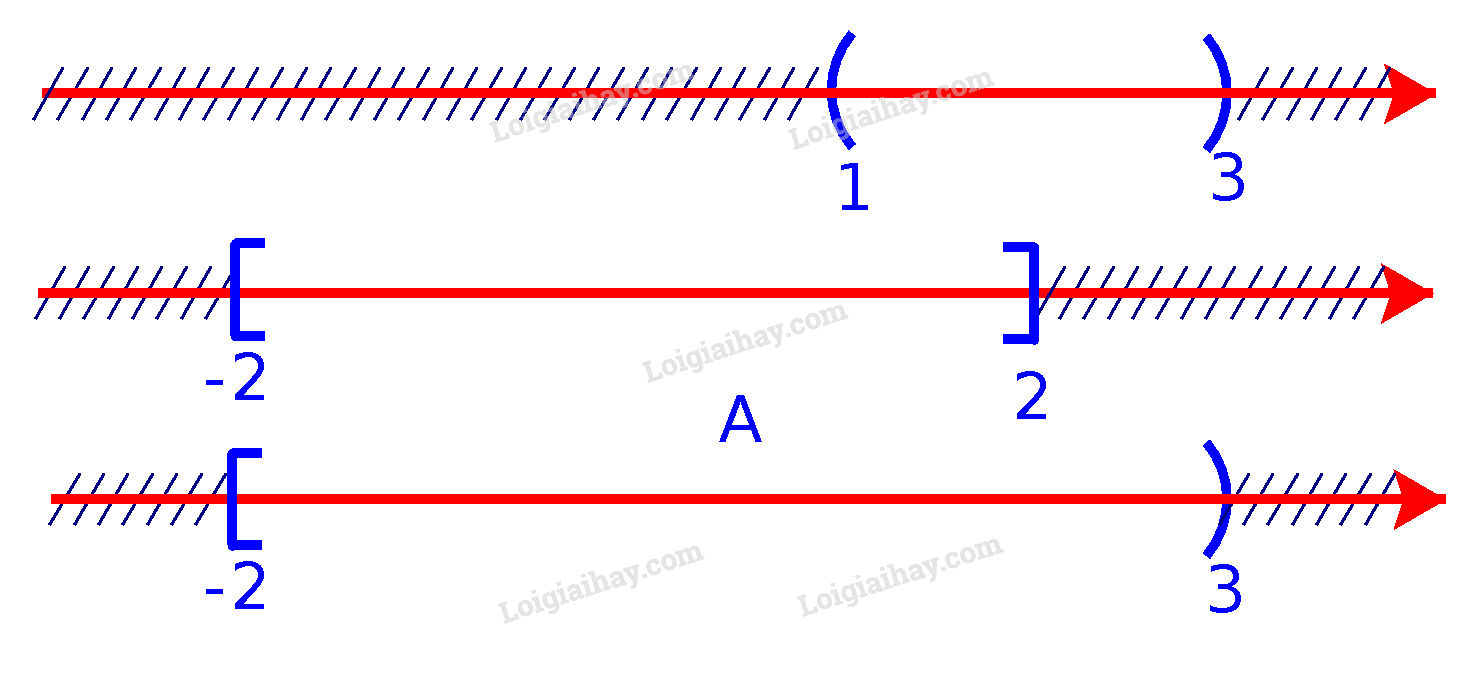
Lời giải chi tiết: a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:
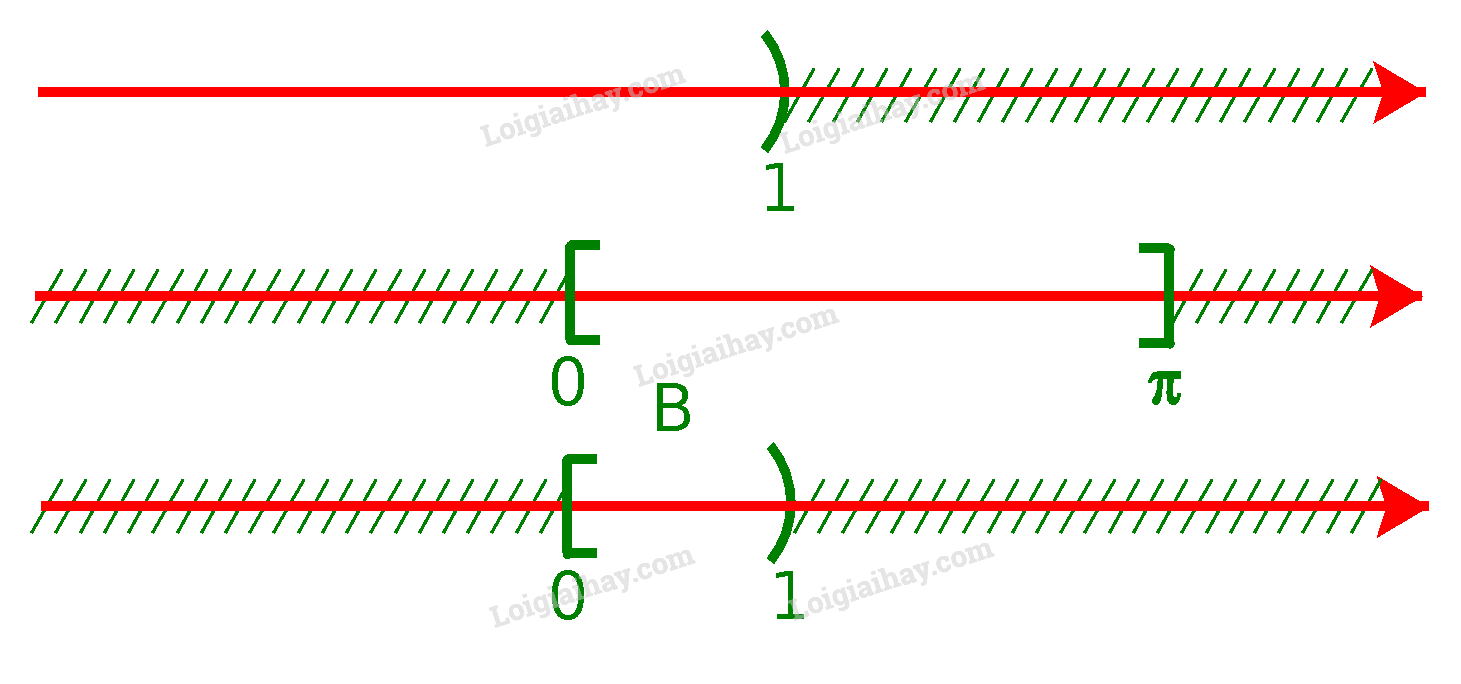
Từ sơ đồ, ta thấy \(A = [ - 2;3)\) b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:
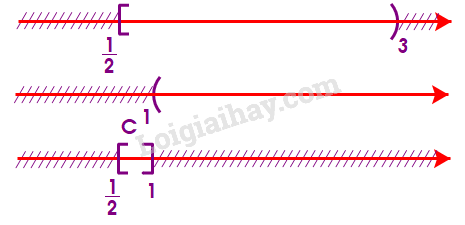
Từ sơ đồ, ta thấy \(B = [0;1)\) c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:
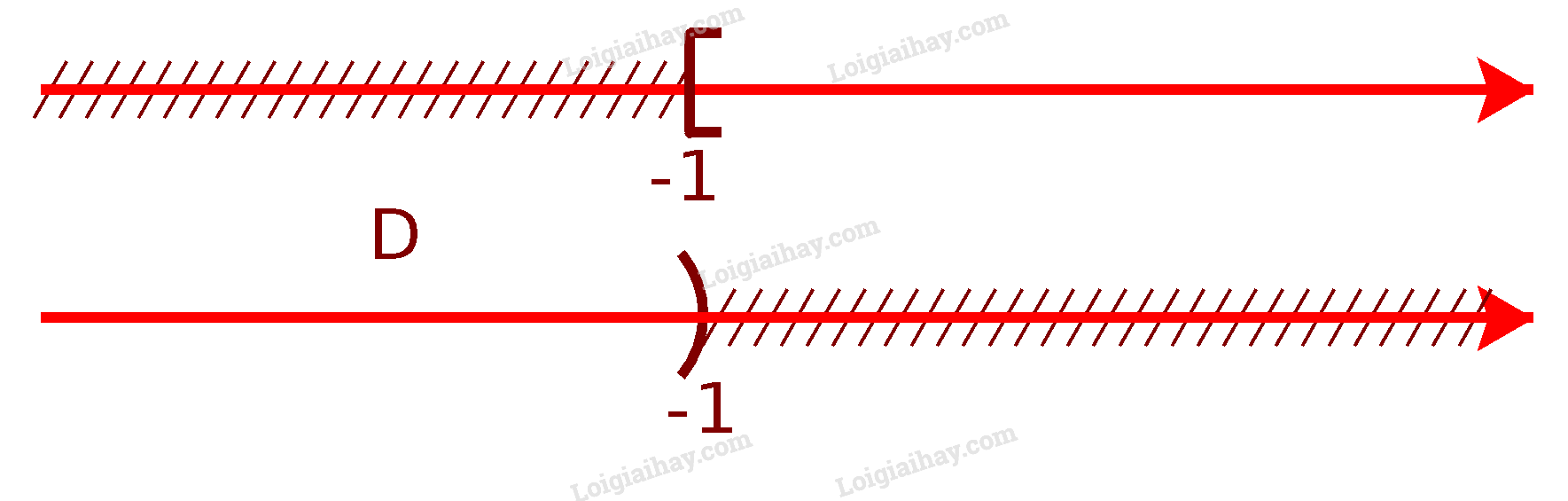
Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\) d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:
Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)
|





















Danh sách bình luận