Giải bài 6 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạoMột người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt dất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là Tổng hợp đề thi giữa kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
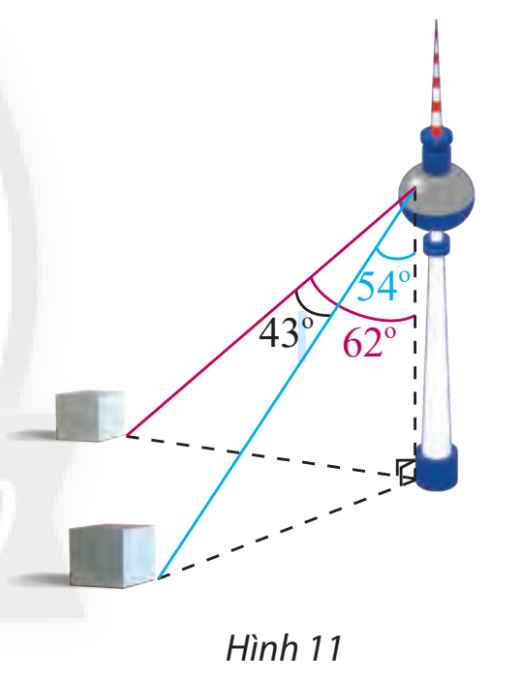
Đề bài Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt dất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là \({43^ \circ }\), góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là \({62^ \circ }\) và đến điểm mốc khác là \({54^ \circ }\)(Hình 11). Tính khoảng cách giữa hai cột mốc này.
Phương pháp giải - Xem chi tiết
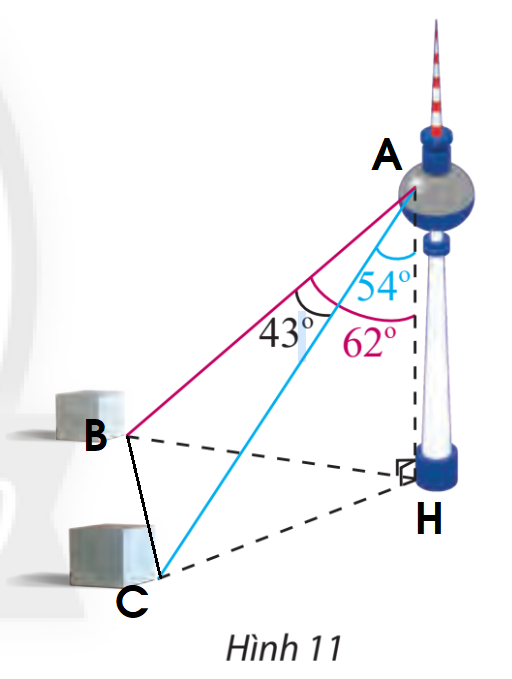
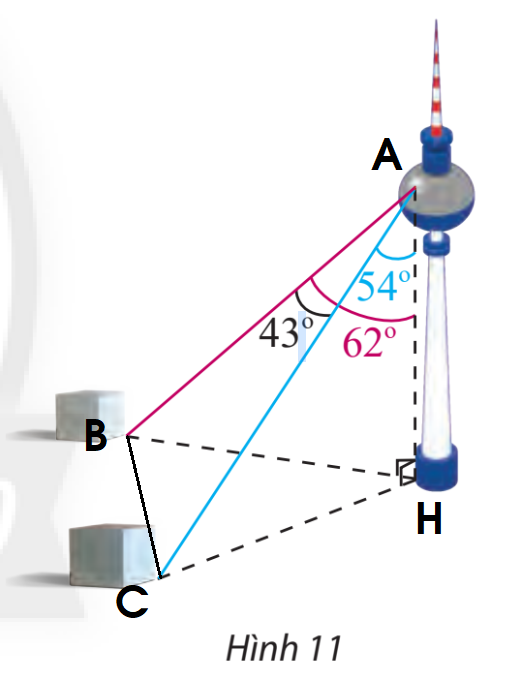
Bước 1: Kí hiệu các điểm A, B, C, H như hình trên. Bước 2: Tính AB, AC bằng cách gắn vào tam giác ABH và ACH. Bước 3: Áp dụng định lí cosin cho tam giác ABC: \(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\) Lời giải chi tiết
Gọi các điểm A, B, C, H như hình trên. Xét tam giác ABH ta có: \(AH = 352,\;\widehat {BAH} = {62^ \circ }\) Mà \(\cos \widehat {BAH} = \frac{{AH}}{{AB}} \Rightarrow AB = 352 : \cos {62^ \circ } \approx 749,78\) Tương tự, ta có: \(\cos \widehat {CAH} = \frac{{AH}}{{AC}} \Rightarrow AC = 352:\cos {54^ \circ } \approx 598,86\) Áp dụng định lí cosin cho tam giác ABC, ta có: \(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {749,78^2} + {598,86^2} - 2.749,78.598,86.\cos {43^ \circ }\\ \Rightarrow BC \approx 513,84\end{array}\) Vậy khoảng cách giữa hai cột mốc này là 513,84 m.
|




















Danh sách bình luận