Giải bài 4 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo

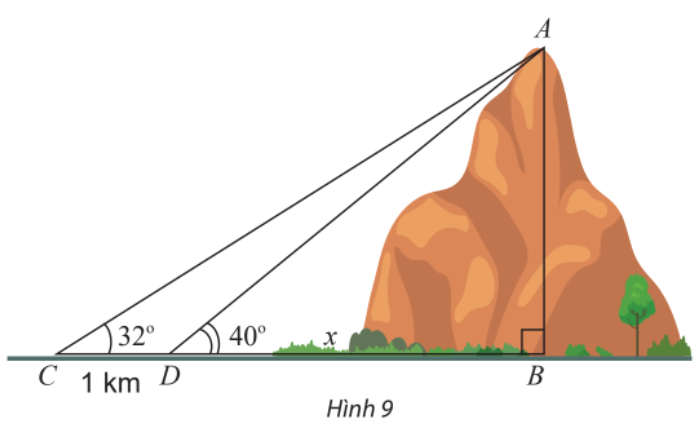
Đề bài

Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là \({32^ \circ }\) và \({40^ \circ }\) (Hình 9).

Lời giải chi tiết

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)

Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)

\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)

\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)

Vậy chiều cao của ngọn núi là 2,45 km.