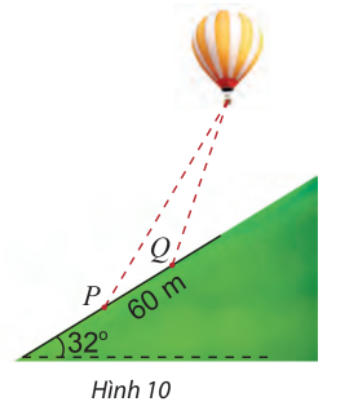
Giải bài 5 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạoHai người quan sát khinh khí cầu tại hai địa điểm P và Q nằm ở sườn đồi nghiêng 32 so với phương ngang, cách nhau 60 m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là Tổng hợp đề thi giữa kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
Đề bài Hai người quan sát khinh khí cầu tại hai địa điểm P và Q nằm ở sườn đồi nghiêng \({32^ \circ }\) so với phương ngang, cách nhau 60 m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là \({62^ \circ }\). Cùng lúc đó, người quan sát tại Q xác định góc nâng của khinh khí cầu đó là \({70^ \circ }\). Tính khoảng cách từ Q đến khinh khí cầu.
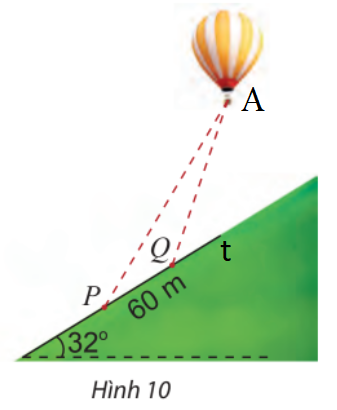
Phương pháp giải - Xem chi tiết Kí hiệu điểm A là vị trí khinh khí cầu. Bước 1: Tính góc P, Q, A trong tam giác APQ. Bước 2: Áp dụng định lí sin, tính QA Lời giải chi tiết
Gọi A là vị trí của khinh khí cầu, Pt là đường sườn đồi như hình. Ta có: Tại P, góc nâng của khinh khí cầu là \({62^ \circ }\)\( \Rightarrow \widehat P = {62^ \circ } - {32^ \circ } = {30^ \circ }\) Tại Q, góc nâng của khinh khí cầu là \({70^ \circ }\)\( \Rightarrow \widehat {AQt} = {70^ \circ } - {32^ \circ } = {38^ \circ }\) \( \Rightarrow \widehat {AQP} = {180^ \circ } - {38^ \circ } = {142^ \circ }\) và \(\widehat A = {180^ \circ } - {142^ \circ } - {30^ \circ } = {8^ \circ }\) Áp dụng định lí sin trong tam giác APQ, ta có: \(\begin{array}{l}\frac{{PQ}}{{\sin A}} = \frac{{QA}}{{\sin P}}\\ \Rightarrow QA = \sin P.\frac{{PQ}}{{\sin A}} = \sin {30^ \circ }.\frac{{60}}{{\sin {8^ \circ }}} \approx 215,56\;(m)\end{array}\) Vậy khoảng cách từ Q đến khinh khí cầu là 215,56 m.
|




















Danh sách bình luận