Giải bài 2 trang 39 SGK Toán 10 tập 1 – Chân trời sáng tạoBiểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ Oxy: Quảng cáo
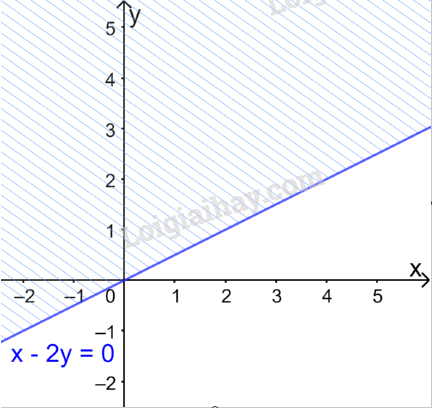
Đề bài Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ Oxy: \(\left\{ \begin{array}{l}x - 2y > 0\\x + 3y < 3\end{array} \right.\) Phương pháp giải - Xem chi tiết Biểu diễn từng miền nghiệm của mỗi bất phương trình trên cùng một mặt phẳng Oxy Lời giải chi tiết Vẽ đường thẳng \(d:x - 2y = 0\) đi qua hai điểm \(O(0;0)\) và \(B\left( {2;1} \right)\) Xét điểm \(A(1;0).\) Ta thấy \(A \notin \Delta \) và \(1 - 2.0 = 1> 0\) Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d\), chứa điểm A (miền không gạch chéo trên hình)
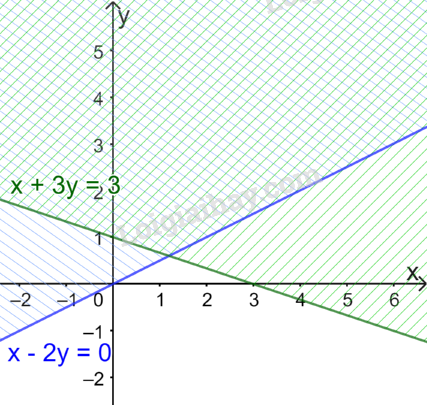
Vẽ đường thẳng \(d':x + 3y = 3\) đi qua hai điểm \(A'(0;1)\) và \(B'\left( {3;0} \right)\) Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 + 3.0 = 0 < 3\) Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d'\), chứa gốc tọa độ O (miền không gạch chéo trên hình)
Vậy miền không gạch chéo trong hình trên là miền nghiệm của hệ bất phương trình đã cho.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
