Đề thi học kì 2 Toán 7 - Đề số 12 - Chân trời sáng tạoPhần trắc nghiệm (3 điểm) Em hãy chọn phương án trả lời đúng Câu 1: Trong các phát biểu sau, phát biểu nào đúng?Đề bài
I. Trắc nghiệm
Câu 1 :
Trong các phát biểu sau, phát biểu nào đúng?
Câu 2 :
Giá trị x thoả mãn tỉ lệ thức: \(\frac{6}{x} = \frac{{ - 10}}{5}\)
Câu 3 :
Trong các công thức sau, công thức nào phát biểu: “Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2”?
Câu 4 :
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài)
Câu 5 :
Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là
Câu 6 :
Giá trị của đa thức \(g\left( x \right) = {x^8}{\rm{ + }}{x^4} + {x^2} + 1\) tại \(x = - 1\) bằng
Câu 7 :
Trong các biến cố sau, biến cố nào là biến cố ngẫu nhiên?
Câu 8 :
Gieo một đồng xu cân đối, đồng chất 1 lần. Xác suất của biến cố “Đồng xu xuất hiện mặt ngửa” là
Câu 9 :
Cho \(\Delta ABC\) vuông tại A có \(\widehat B = {65^0}.\) Chọn khẳng định đúng.
Câu 10 :
Cho tam giác \(ABC\) có AM là đường trung tuyến, trọng tâm \(G\). Khẳng định nào sau đây đúng?
Câu 11 :
Bộ ba số nào là độ dài ba cạnh của một tam giác?
Câu 12 :
Cho \(\Delta ABC\) có \(\widehat A = {35^0};\widehat B = {45^0}\). Số đo góc C là:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Trong các phát biểu sau, phát biểu nào đúng?
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về tỉ lệ thức. Lời giải chi tiết :
Ta có: \(\frac{1}{2} = \frac{2}{4} \ne \frac{{ - 2}}{4}\) nên A sai. \(\frac{1}{2} = \frac{5}{{10}}\) nên B đúng. \(\frac{1}{2} = \frac{2}{4} \ne \frac{3}{4}\) nên C sai. \(\frac{1}{2} = \frac{{ - 3}}{{ - 6}} \ne \frac{{ - 2}}{{ - 6}}\) nên D sai. Đáp án B.
Câu 2 :
Giá trị x thoả mãn tỉ lệ thức: \(\frac{6}{x} = \frac{{ - 10}}{5}\)
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về tỉ lệ thức: Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\). Lời giải chi tiết :
Ta có: \(\frac{6}{x} = \frac{{ - 10}}{5}\) nên \(\begin{array}{l}6.5 = \left( { - 10} \right).x\\x = \frac{{6.5}}{{ - 10}}\\x = - 3\end{array}\) Đáp án B.
Câu 3 :
Trong các công thức sau, công thức nào phát biểu: “Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2”?
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về hai đại lượng tỉ lệ thuận: Nếu đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ là a thì ta có công thức \(y = ax\) Lời giải chi tiết :
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2 nên y = 2x. Đáp án A.
Câu 4 :
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài)
Đáp án : D Phương pháp giải :
Sử dụng công thức tính diện tích hình thang để viết biểu thức. Lời giải chi tiết :
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài) là: \(\frac{{\left( {a + b} \right).h}}{2}\). Đáp án D.
Câu 5 :
Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là
Đáp án : A Phương pháp giải :
Hệ số của hạng tử bậc 0 gọi là hệ số tự do của đa thức đó. Lời giải chi tiết :
Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là – 22. Đáp án A.
Câu 6 :
Giá trị của đa thức \(g\left( x \right) = {x^8}{\rm{ + }}{x^4} + {x^2} + 1\) tại \(x = - 1\) bằng
Đáp án : D Phương pháp giải :
Thay \(x = - 1\) vào đa thức để tính giá trị. Lời giải chi tiết :
Thay \(x = - 1\) vào đa thức g(x) ta được: \(g\left( x \right) = {\left( { - 1} \right)^8}{\rm{ + }}{\left( { - 1} \right)^4} + {\left( { - 1} \right)^2} + 1 = 1 + 1 + 1 + 1 = 4\) Đáp án D.
Câu 7 :
Trong các biến cố sau, biến cố nào là biến cố ngẫu nhiên?
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về các loại biến cố. Lời giải chi tiết :
Biến cố “Gieo hai con xúc xắc 1 lần, tổng số chấm xuất hiện trên hai con xúc xắc là 7” là biến cố ngẫu nhiên. Đáp án D.
Câu 8 :
Gieo một đồng xu cân đối, đồng chất 1 lần. Xác suất của biến cố “Đồng xu xuất hiện mặt ngửa” là
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về xác suất của các biến cố đồng khả năng. Lời giải chi tiết :
Do đồng xu cân đối nên biến cố “Đồng xu xuất hiện mặt ngửa” và “Đồng xu xuất hiện mặt sấp” là đồng khả năng nên xác suất của 2 biến cố này bằng nhau và bằng \(\frac{1}{2}\). Đáp án C.
Câu 9 :
Cho \(\Delta ABC\) vuông tại A có \(\widehat B = {65^0}.\) Chọn khẳng định đúng.
Đáp án : B Phương pháp giải :
Dựa vào mối quan hệ giữa góc và cạnh đối nhau trong một tam giác và định lí tổng ba góc của một tam giác bằng \({180^0}\). Lời giải chi tiết :
Tam giác ABC vuông tại A có \(\widehat B = {65^0}\) nên \(\widehat C = {180^0} - \widehat A - \widehat B = {180^0} - {90^0} - {65^0} = {25^0}\). Vì \(\widehat A > \widehat B > \widehat C\left( {{{90}^0} > {{65}^0} > {{25}^0}} \right)\) nên \(BC > AC > AB\). Đáp án B.
Câu 10 :
Cho tam giác \(ABC\) có AM là đường trung tuyến, trọng tâm \(G\). Khẳng định nào sau đây đúng?
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về trọng tâm của tam giác. Lời giải chi tiết :
Vì G là trọng tâm của tam giác ABC nên \(AG = \frac{2}{3}AM\) suy ra \(GM = AM - AG = AM - \frac{2}{3}AM = \frac{1}{3}AM\). Suy ra \(\frac{{GM}}{{AG}} = \frac{{\frac{1}{3}AM}}{{\frac{2}{3}AM}} = \frac{1}{2}\) hay \(AG = 2GM\). Đáp án B.
Câu 11 :
Bộ ba số nào là độ dài ba cạnh của một tam giác?
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa các cạnh của một tam giác. Lời giải chi tiết :
Ta có: 4 + 5 = 9 < 10, ba độ dài \(4cm,\;5cm,\;10cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác. 5 + 5 = 10 < 12, ba độ dài \(5cm,\;5cm,\;12cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác. 11 > 20 – 11 = 9, ba độ dài \(11cm,\;11cm,\;20cm\) thỏa mãn điều kiện của bất đẳng thức tam giác nên đây có thể là độ dài ba cạnh của một tam giác. 11 = 20 – 9, ba độ dài \(9cm,\;20cm,\;11cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác. Đáp án C.
Câu 12 :
Cho \(\Delta ABC\) có \(\widehat A = {35^0};\widehat B = {45^0}\). Số đo góc C là:
Đáp án : D Phương pháp giải :
Dựa vào định lí tổng ba góc của một tam giác bằng \({180^0}\). Lời giải chi tiết :
Số đo góc C là: \(\begin{array}{l}\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {35^0} - {45^0}\\ = {100^0}\end{array}\) Đáp án D.
II. Tự luận
Phương pháp giải :
a) Thay \(x = - 2,\;y = \frac{1}{3}\) vào A để tính giá trị biểu thức. b) Sử dụng các phép tính với đa thức một biến để tìm giá trị của x. Lời giải chi tiết :
a) Tại \(x = - 2,\;y = \frac{1}{3}\) ta có \(\begin{array}{l}A = \left[ {2 \cdot ( - 2) + \frac{1}{3}} \right]\left[ {2 \cdot ( - 2) - \frac{1}{3}} \right]\\ = \left( { - 4 + \frac{1}{3}} \right)\left( { - 4 - \frac{1}{3}} \right)\\ = \frac{{ - 11}}{3}.\frac{{ - 13}}{3}\\ = \frac{{143}}{9}.\end{array}\) b) \(x(3x - 2) - 3{x^2} = \frac{3}{4}\) \(\begin{array}{l}3{x^2} - 2x - 3{x^2} = \frac{3}{4}\\ - 2x = \frac{3}{4}\\x = \frac{{ - 3}}{8}.\end{array}\) Vậy \(x = \frac{{ - 3}}{8}\). Phương pháp giải :
Gọi số tấm thiệp của ba lớp 7A, 7B, 7C lần lượt là \(x,y,z\left( {x,y,z \in {\mathbb{N}^ * }} \right)\) Viết phương trình dựa vào đề bài. Áp dụng tính chất dãy tỉ số bằng nhau để tìm x, y, z. Lời giải chi tiết :
Gọi số tấm thiệp của ba lớp 7A, 7B, 7C lần lượt là \(x,y,z\left( {x,y,z \in {\mathbb{N}^ * }} \right)\) Vì có 40 tấm thiệp nên x + y + z = 40 Vì số học sinh tỉ lệ với số thiệp cần làm nên ta có \(\frac{x}{{45}} = \frac{y}{{42}} = \frac{z}{{33}}\). Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\frac{x}{{45}} = \frac{y}{{42}} = \frac{z}{{33}} = \frac{{x + y + z}}{{45 + 42 + 33}} = \frac{{40}}{{120}} = \frac{1}{3}\) suy ra \( x = \frac{1}{3}.45 = 15; y = \frac{1}{3}.42 = 14; z = \frac{1}{3}.33 = 11\) Vậy số tấm thiệp của ba lớp 7A, 7B, 7C lần lượt là 15; 14; 11. Phương pháp giải :
Thực hiện tính toán với đa thức một biến. Lời giải chi tiết :
a) \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) \(\begin{array}{l} = 5{x^4} + \left( { - 7{x^2} - 6{x^2}} \right) + \left( { - 3x + 11x} \right) - 30\\ = 5{x^4} - 13{x^2} + 8x - 30\end{array}\) \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\) \(\begin{array}{l} = 13{x^4} + \left( { - 11{x^3} + 20{x^3}} \right) + \left( {5x - 34x} \right) + \left( { - 10 - 2} \right)\\ = 13{x^4} + 9{x^3} - 29x - 12\end{array}\) b) \(A\left( x \right) - B\left( x \right) = \left( {5{x^4} - 13{x^2} + 8x - 30} \right) - \left( {13{x^4} + 9{x^3} - 29x - 12} \right)\) \(\begin{array}{l} = 5{x^4} - 13{x^2} + 8x - 30 - 13{x^4} - 9{x^3} + 29x + 12\\ = \left( {5{x^4} - 13{x^4}} \right) - 9{x^3} - 13{x^2} + \left( {8x + 29x} \right) + \left( { - 30 + 12} \right)\\ = -8{x^4} - 9{x^3} - 13{x^2} + 37x - 18\end{array}\) Phương pháp giải :
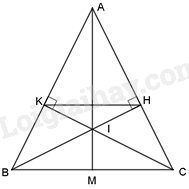
a) Chứng minh \(\Delta ABH = \Delta ACK\) theo trường hợp cạnh huyền – góc nhọn. suy ra AH = AK nên tam giác AKH là tam giác cân. b) Chứng minh \(\widehat {{P_1}} = \widehat {{N_1}}\) nên \(\Delta AKI = \Delta AHI\) theo trường hợp cạnh huyền – cạnh góc vuông suy ra \(\widehat {AIK} = \widehat {AIH}\) Từ đó ta có \(\widehat {CIM} = \widehat {BIM}\) nên IM là phân giác của góc BIC c) Từ tam giác cân ABC và AHK ta có \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\), \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) nên \(\widehat {ABC} = \widehat {AKH}\). Mà hai góc này ở vị trí đồng vị nên HK // BC. Lời giải chi tiết :
a) Xét \(\Delta ABH\) và \(\Delta ACK\) có: \(\widehat {AHB} = \widehat {AKC} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\)) AB = AC (\(\Delta ABC\) cân); góc A chung; Do đó: \(\Delta ABH = \Delta ACK\) (cạnh huyền – góc nhọn). \( \Rightarrow AH = AK \Rightarrow \Delta AHK\) cân tại A (đpcm). b) Xét \(\Delta AKI\) và \(\Delta AHI\) có: \(\widehat {AKI} = \widehat {AHI} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\)) AK = AH (\(\Delta AHK\) cân tại A); cạnh AI chung; Do đó: \(\Delta AKI = \Delta AHI\) (cạnh huyền – cạnh góc vuông). \( \Rightarrow \widehat {AIK} = \widehat {AIH}\). Mà: \(\widehat {AIK} = \widehat {CIM};\widehat {AIH} = \widehat {BIM}\) (2 góc đối đỉnh). Do đó: \(\widehat {CIM} = \widehat {BIM}\)\( \Rightarrow IM\)là phân giác của góc BIC (đpcm). c) \(\Delta ABC\) cân tại A nên: \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\) . \(\Delta AHK\) cân tại A nên: \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) . Suy ra \(\widehat {ABC} = \widehat {AKH}\). Mà 2 góc này ở vị trí đồng vị. Do đó: KH // BC (đpcm). Phương pháp giải :
Biến đổi \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\) thành \(\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4}\). Áp dụng tính chất dãy tỉ số bằng nhau để suy ra \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2} = 0\) Từ đó ta có \(6z = 12x = 8y\). Đặt \(6z = 12x = 8y = 24k\left( {k > 0} \right) \Rightarrow \left( {x;y;z} \right) = \left( {2k;3k;4k} \right)\) Tìm k dựa vào \(200 < {y^2} + {z^2} < 450\) Từ đó tính được x, y, z. Lời giải chi tiết :
Ta có \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\) nên \(\begin{array}{l}\frac{{3\left( {2z - 4x} \right)}}{{3.3}} = \frac{{4\left( {3x - 2y} \right)}}{{4.4}} = \frac{{2\left( {4y - 3z} \right)}}{{2.2}}\\\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4}\end{array}\) Áp dụng tính chất dãy tỉ số bằng nhau, ta có: \(\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4} = \frac{{6z - 12x + 12x - 8y + 8y - 6z}}{{9 + 16 + 4}} = \frac{0}{{29}} = 0\) Do đó \(\left\{ \begin{array}{l}6z - 12x = 0\\12x - 8y = 0\\8y - 6z = 0\end{array} \right.\) hay \(6z = 12x = 8y\). Đặt \(6z = 12x = 8y = 24k\left( {k > 0} \right)\) ta được \(\left( {x;y;z} \right) = \left( {2k;3k;4k} \right)\) Theo giả thiết \(200 < {y^2} + {z^2} < 450\) nên \(200 < (3k)^2 + (4k)^2 < 450\) \(200 < 9{k^2} + 16{k^2} < 450\) suy ra \(200 < 25{k^2} < 450\) \(8 < k^2 < 18\) Do đó \(k \in \left\{ {3;4} \right\}\) Từ đó tìm được \(\left( {x;y;z} \right) \in \left\{ {\left( {6;9;12} \right);\left( {8;12;16} \right)} \right\}\)
|






















Danh sách bình luận