Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 8Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... Đề bài
I. Trắc nghiệm
Câu 1 :
Nếu 2.b = 5.c và b, c ≠ 0 thì:
Câu 2 :
Với \(a,b,c,d \in Z;{\rm{ }}b,d \ne 0\) kết luận nào sau đây là đúng?
Câu 3 :
Cho y là đại lượng tỉ lệ thuận với x theo hệ số tỉ lệ k, ta có:
Câu 4 :
Cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x = 4 thì y = -15. Hệ số tỉ lệ của y đối với x là:
Câu 5 :
Cho y = 10x thì ta nói
Câu 6 :
Cho tam giác ABC có độ dài ba cạnh là ba số nguyên. Biết AB = 3 cm; AC = 7 cm. Khi đó độ dài cạnh BC không thể bằng
Câu 7 :
Cho \(\Delta ABC\) cân tại B. Khi đó:
Câu 8 :
Cho \(\Delta ABC\) vuông tại A và \(\hat B = {60^0}\). Khi đó:
Câu 9 :
Cho \(\Delta MNP\) có MN < MP < NP. Trong các khẳng định sau, câu nào đúng?
II. Tự luận
Câu 1 :
Cho hai đại lượng x và y tỉ lệ thuận với nhau và khi x = 5 thì y = -4. a) Tìm hệ số tỉ lệ k trong công thức \(y = kx\). b) Biểu diễn y theo x. c) Tính giá trị của y khi x = -10; x = 2.
Câu 2 :
Cho tam giác ABC có số đo các góc A, B, C lần lượt ti lệ với các số 2; 4; 6. a) Tính số đo các góc của tam giác ABC. b) Sắp xếp các cạnh của tam giác ABC theo thứ tự từ bé đến lớn.
Câu 3 :
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt AC tại D. Từ D kẻ DH vuông góc với BC. a) So sánh BA và BC. b) Chứng minh DA = DH. c) So sánh DC và DA.
Câu 4 :
Ba đội cùng chuyển một khối lượng gạch như nhau. Thời gian để đội thứ nhất, đội thứ hai và đội thứ ba làm xong công việc lần lượt là 2 giờ, 3 giờ, 4 giờ. Tính số người tham gia làm việc của mỗi đội, biết rằng số người của đội thứ ba ít hơn số người của đội thứ hai là 5 người. Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Nếu 2.b = 5.c và b, c ≠ 0 thì:
Đáp án : B Phương pháp giải :
Dựa vào tính chất của tỉ lệ thức: Nếu \(ad = bc\left( {a,b,c,d \ne 0} \right)\) thì ta có các tỉ lệ thức: \(\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{d}{b} = \frac{c}{a};\frac{d}{c} = \frac{b}{a}\) Lời giải chi tiết :
Nếu \(2.b = 5.c\) thì ta có các tỉ lệ thức: \(\frac{2}{c} = \frac{5}{b};\frac{2}{5} = \frac{c}{b};\frac{c}{2} = \frac{b}{5};\frac{5}{2} = \frac{b}{c}\) nên B đúng.
Câu 2 :
Với \(a,b,c,d \in Z;{\rm{ }}b,d \ne 0\) kết luận nào sau đây là đúng?
Đáp án : C Phương pháp giải :
Dựa vào tính chất dãy tỉ số bằng nhau. Lời giải chi tiết :
Với \(a,b,c,d \in Z;{\rm{ }}b,d \ne 0\) ta có: \(\frac{a}{b} = \frac{c}{d} = \frac{{a - c}}{{b - d}}\).
Câu 3 :
Cho y là đại lượng tỉ lệ thuận với x theo hệ số tỉ lệ k, ta có:
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận. Lời giải chi tiết :
y là đại lượng tỉ lệ thuận với x theo hệ số tỉ lệ k nên ta có công thức \(y = kx\).
Câu 4 :
Cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x = 4 thì y = -15. Hệ số tỉ lệ của y đối với x là:
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch. Lời giải chi tiết :
x và y là hai đại lượng tỉ lệ nghịch và khi x = 4 thì y = -15 nên hệ số tỉ lệ của y đối với x là: k = 4.(-15) = -60.
Câu 5 :
Cho y = 10x thì ta nói
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận và tỉ lệ nghịch. Lời giải chi tiết :
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = 10x thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ 10.
Câu 6 :
Cho tam giác ABC có độ dài ba cạnh là ba số nguyên. Biết AB = 3 cm; AC = 7 cm. Khi đó độ dài cạnh BC không thể bằng
Đáp án : A Phương pháp giải :
Dựa vào quan hệ giữa ba cạnh của một tam giác. Lời giải chi tiết :
Vì 3 + 4 = 7 nên 3cm; 4cm; 7cm không thể là ba cạnh của tam giác ABC hay BC không thể bằng 4cm.
Câu 7 :
Cho \(\Delta ABC\) cân tại B. Khi đó:
Đáp án : B Phương pháp giải :
Dựa vào tính chất của tam giác cân. Lời giải chi tiết :
Tam giác ABC cân tại B nên \(\widehat A = \widehat C\).
Câu 8 :
Cho \(\Delta ABC\) vuông tại A và \(\hat B = {60^0}\). Khi đó:
Đáp án : C Phương pháp giải :
Dựa vào định lí tổng ba góc của một tam giác. Lời giải chi tiết :
Xét tam giác ABC vuông tại A nên \(\widehat A = {90^0}\) có: \(\widehat A + \widehat B + \widehat C = {180^0}\) suy ra \(\widehat C = {180^0} - {90^0} - {60^0} = {30^0}\).
Câu 9 :
Cho \(\Delta MNP\) có MN < MP < NP. Trong các khẳng định sau, câu nào đúng?
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa góc và cạnh đối diện trong tam giác. Lời giải chi tiết :
\(\Delta MNP\) có MN < MP < NP nên \(\widehat P < \widehat N < \widehat M\).
Đáp án : D Phương pháp giải :
Dựa vào các đỉnh tương ứng của hai tam giác bằng nhau. Lời giải chi tiết :
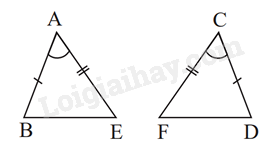
Xét tam giác ABE và tam giác CDF có: \(\begin{array}{l}AB = CD\\\widehat {BAE} = \widehat {DCF}\\AE = CF\end{array}\) \(\Delta ABE = \Delta CDF\) (c.g.c)
Đáp án : A Phương pháp giải :
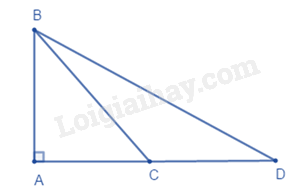
Đoạn thẳng ngắn nhất trong các đoạn thẳng kẻ từ B đến AD là khoảng cách từ điểm B đến đường thẳng AD. Lời giải chi tiết :
Độ dài đoạn thẳng AB là khoảng cách từ điểm B đến đường thẳng AD.
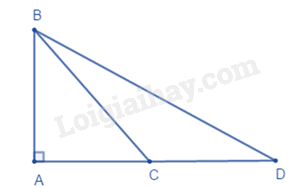
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa đường xiên và hình chiếu. Lời giải chi tiết :
Vì AB < AD, C nằm giữa A và D nên AC < AD. Do đó AB < BC < BD. (quan hệ giữa đường xiên và hình chiếu)
II. Tự luận
Câu 1 :
Cho hai đại lượng x và y tỉ lệ thuận với nhau và khi x = 5 thì y = -4. a) Tìm hệ số tỉ lệ k trong công thức \(y = kx\). b) Biểu diễn y theo x. c) Tính giá trị của y khi x = -10; x = 2. Phương pháp giải :
a) Dựa vào kiến thức về hai đại lượng tỉ lệ thuận để tìm k. b) Viết công thức biểu diễn y theo x với k vừa tìm được. c) Thay giá trị của x vào công thức biểu diễn để tìm y Lời giải chi tiết :
a) Vì hai đại lượng x và y tỉ lệ thuận với nhau và khi x = 5 thì y = -4 nên ta có: \( - 4 = k.5\) suy ra \(k = \frac{{ - 4}}{5}\). b) Công thức biểu diễn y theo x là: \(y = \frac{{ - 4}}{5}x\). c) Thay x = -10 vào công thức ta được: \(y = \frac{{ - 4}}{5}.\left( { - 10} \right) = 8\). Thay x = 2 vào công thức ta được: \(y = \frac{{ - 4}}{5}.2 = \frac{{ - 8}}{5}\).
Câu 2 :
Cho tam giác ABC có số đo các góc A, B, C lần lượt ti lệ với các số 2; 4; 6. a) Tính số đo các góc của tam giác ABC. b) Sắp xếp các cạnh của tam giác ABC theo thứ tự từ bé đến lớn. Phương pháp giải :
a) Áp dụng tính chất của dãy tỉ số bằng nhau để tìm số đo các góc của tam giác ABC. b) Dựa vào quan hệ giữa góc và cạnh đối diện trong một tam giác. Lời giải chi tiết :
a) Ta có tam giác ABC có số đo của các góc A, B,C lần lượt tỉ lệ với các số 2; 4; 6 nên ta có: \(\frac{{\widehat A}}{2} = \frac{{\widehat B}}{4} = \frac{{\widehat C}}{6}\) Áp dụng tính chất dãy tỉ số bằng nhau, ta có: \(\frac{{\widehat A}}{2} = \frac{{\widehat B}}{4} = \frac{{\widehat C}}{6} = \frac{{\widehat A + \widehat B + \widehat C}}{{2 + 4 + 6}} = \frac{{{{180}^0}}}{{12}} = {15^0}\) Suy ra \(\begin{array}{l}\widehat A = {15^0}.2 = {30^0}\\\widehat B = {15^0}.4 = {60^0}\\\widehat C = {15^0}.6 = {90^0}\end{array}\) Vậy số đo của góc A, B, C lần lượt là \({30^0};{60^0};{90^0}\). b) Xét \(\Delta ABC\) có \(\widehat A < \widehat B < \widehat C\left( {{{30}^0} < {{60}^0} < {{90}^0}} \right)\) nên \(BC < AC < AB\). Vậy các cạnh của tam giác ABC theo thứ tự từ bé đến lớn là BC, AC, AB.
Câu 3 :
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt AC tại D. Từ D kẻ DH vuông góc với BC. a) So sánh BA và BC. b) Chứng minh DA = DH. c) So sánh DC và DA. Phương pháp giải :
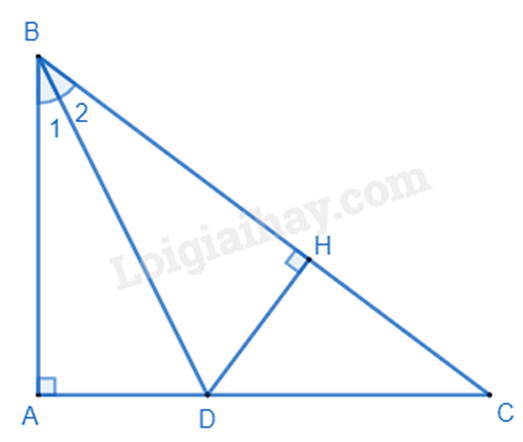
a) Dựa vào quan hệ giữa đường vuông góc và đường xiên. b) Chứng minh \(\Delta ABD = \Delta HBD\) nên DA = DH. c) So sánh DC và DH dựa vào quan hệ giữa các cạnh trong tam giác, mà DH = DA nên so sánh được DC và DA. Lời giải chi tiết :
a) Xét tam giác ABC vuông tại A nên BA là đường vuông góc kẻ từ B đến AC, BC là đường xiên kẻ từ B đến AC nên BA < BC. (quan hệ giữa đường vuông góc và đường xiên. b) Xét tam giác ABD và HBD, ta có: \(\widehat {BAD} = \widehat {BHD} = {90^0}\) \(\widehat {{B_1}} = \widehat {{B_2}}\) (BD là tia phân giác của góc ABC) BD chung Suy ra \(\Delta ABD = \Delta HBD\) (cạnh huyền – góc nhọn) Suy ra DA = DH (hai cạnh tương ứng) (đpcm) c) Trong tam giác DHC có \(\widehat {DHC} = {90^0}\) Suy ra DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) Mà DA = DH (cmt) Suy ra DA < DC.
Câu 4 :
Ba đội cùng chuyển một khối lượng gạch như nhau. Thời gian để đội thứ nhất, đội thứ hai và đội thứ ba làm xong công việc lần lượt là 2 giờ, 3 giờ, 4 giờ. Tính số người tham gia làm việc của mỗi đội, biết rằng số người của đội thứ ba ít hơn số người của đội thứ hai là 5 người. Phương pháp giải :
Áp dụng tính chất của hai đại lượng tỉ lệ nghịch. Áp dụng tính chất dãy tỉ số bằng nhau để tính x, y, z. Lời giải chi tiết :
Gọi số công dân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là x, y, z. \(\left( {x,y,z \in \mathbb{N}*,y > z} \right)\) Số công nhân của đội thứ ba ít hơn số công nhân của đội thứ hai là 5 người nên \(y - z = 5\). Với cùng một khối lượng công việc, số công nhân tham gia làm việc và thời gian hoàn thành công việc của mỗi đội là hai đại lượng tỉ lệ nghịch với nhau. Do đó, ta có: 2x = 3y = 4z. Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\frac{x}{6} = \frac{y}{4} = \frac{z}{3} = \frac{{y - z}}{{4 - 3}} = \frac{5}{1} = 5\) Suy ra \(\begin{array}{l}x = 5.6 = 30\\y = 5.4 = 20\\z = 5.3 = 15\end{array}\) Vậy số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là 30, 20, 15 người.
|
