Đề thi giữa kì 1 Toán 7 - Đề số 6

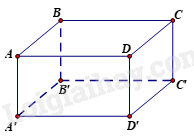
Đề bài

Phần trắc nghiệm (3 điểm)

Câu 1. Chọn khẳng định đúng

A. \(9 \notin Z\)

B. \(\frac{{ - 1}}{3}\; \in Q\)

C. \( - 5 \in I\)

D. \(2,5\; \in Z\)

Câu 2. Số đối của \(\frac{{ - 8}}{9}\) là số nào?

A. \(\frac{9}{8}\).

B. \(\frac{9}{{ - 8}}\).

C. \( - \frac{8}{9}\).

D. \(\frac{8}{9}\).

Câu 3.  Hãy sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn: \(\,\frac{{ - 15}}{{ - 17}};\,0;\,\frac{{25}}{{17}}; - \frac{3}{{17}}\)  ?

A. \( - \frac{3}{{17}};0;\,\frac{{25}}{{17}};\,\frac{{ - 15}}{{ - 17}}\).

B. \(\frac{{25}}{{17}};\,0;\frac{{ - 15}}{{ - 17}};\, - \frac{3}{{17}}\).

C. \( - \frac{3}{{17}};0;\,\frac{{ - 15}}{{ - 17}};\frac{{25}}{{17}}\).

D. \(\frac{{25}}{{17}};\,\frac{{ - 15}}{{ - 17}};\,0;\, - \frac{3}{{17}}\).

Câu 4. Quan sát trục số sau. Khẳng định nào sau đây đúng?

A. Điểm \(A\) biểu diễn số hữu tỉ \(\frac{1}{2}\).

B. Điểm \(B\) biểu diễn số hữu tỉ \(2\).

C. Điểm \(C\) biểu diễn số hữu tỉ \(\frac{1}{2}\).

D. Điểm A biểu diễn số hữu tỉ \(\frac{{ - 1}}{2}\).

Câu 5. Hình hộp chữ nhật có bao nhiêu cạnh?

A. 9 cạnh.

B. 10 cạnh.

C. 11 cạnh.

D. 12 cạnh.

Câu 6. Ở mỗi đỉnh của hình lập phương có bao nhiêu góc?

A. 3 góc bẹt.

B. 3 góc vuông.

C. Không có góc nào.

D. 5 góc.

Câu 7. Đường chéo của hình hộp chữ nhật \(ABCD.A'B'C'D'\) là đường nào?

A. \(A'D\).

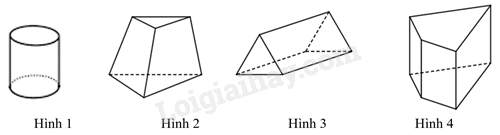
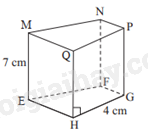
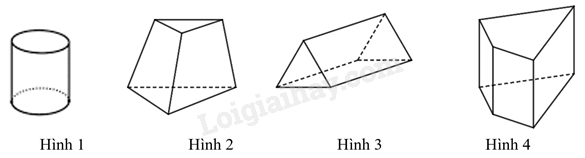
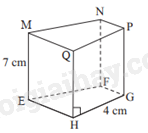
B. \(BC'\).

C. \(AC'\).

D. \(BD\).

Câu 8. Hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(BC = 7\,{\rm{cm}}\). Khẳng định nào sau đây sai?

A. B’C’= 7 cm.

B. \(AD = 7\,{\rm{cm}}\).

C. \(A'D' = 7\,{\rm{cm}}\).

D. \(E'B = 7\,{\rm{cm}}\).

Câu 9. Trong các hình sau, hình nào là hình lăng trụ đứng tam giác

A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4

Câu 10. Cho hình lăng trụ đứng tứ giác \(MNPQ.EFGH\) có cạnh \(ME = 7\,{\rm{cm}}\),\(HG = 4\,{\rm{cm}}\). Khẳng định nào sau đây đúng?

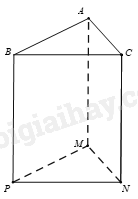
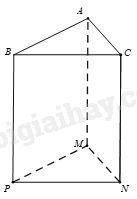
A. \(NF = 7\,{\rm{cm}}\).

B. \(NF = 4\,{\rm{cm}}\).

C. \(EH = 4\,{\rm{cm}}\).

D. \(NP = 7\,{\rm{cm}}\).

Câu 11. Các mặt bên của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là những hình gì?

A. Tam giác.

B. Tứ giác.

C. Hình chữ nhật.

D. Hình vuông.

Câu 12. Cho hình lăng trụ đứng tam giác như hình bên. Mặt đáy của lăng trụ đứng là:

A. ABC.

B. ABPM.

C. ACMN.

D. BCPN.

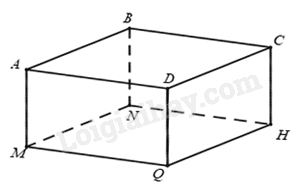
Phần tự luận (7 điểm)

Bài 1. (0,75 điểm). Trong các số 2,5; 0; \( - \frac{1}{3}\), \(1\frac{1}{2}\) số nào là số hữu tỉ dương? Vì sao?

Bài 2. (1,5 điểm). Thực hiện phép tính:

a. \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\);

b. \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\);

c. \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\)

Bài 3. (1,5 điểm).  Tìm số hữu tỉ \(x\), biết:

a. \(25\% - x = 1\frac{5}{6}\);

b. \(\frac{{ - 5}}{4} + \frac{2}{3}:x = 0,75\).

Bài 4. (1,0 điểm). Cho hình hộp chữ nhật ABCD.MNHQ như hình vẽ, có AB = 5cm, BC = 7cm, AM = 3cm Tính diện tích xung quanh và thể tích của hình hộp chữ nhật này.

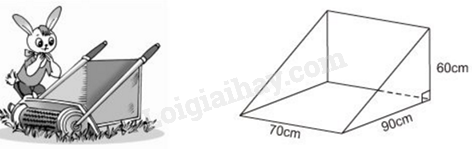
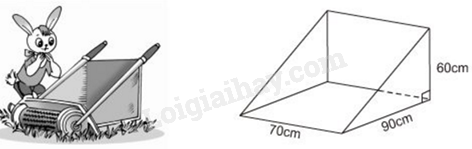
Bài 5. (0,75 điểm). Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác. Hãy tính thể tích của thùng.

Bài 6. (0,5 điểm). Một căn phòng hình hộp chữ nhật có chiều dài \(4,5m\), chiều rộng \(4m\) , chiều cao \(3m\).  Người ta muốn lăn sơn trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là \(11\,{m^2}\). Tính diện tích cần lăn sơn ?

Bài 7. (1,0 điểm). Một cửa hàng bán quần áo có chương trình khuyến mãi như sau: Khách hàng có thẻ thành viên sẽ được giảm 15% tổng số tiền của hóa đơn. Bạn Bình có thẻ thành viên, bạn mua hai chiếc áo sơ mi, mỗi áo đều có giá 200 000 đồng và một quần Jeans với giá 350 000 đồng. Bạn đưa cho người thu ngân 1 triệu đồng. Hỏi bạn Bình được trả lại bao nhiêu tiền?

-------- Hết --------

Lời giải

Phần trắc nghiệm (3 điểm)

Câu 1. Chọn khẳng định đúng

Phương pháp

Dựa vào khái niệm các tập hợp đã học.

Lời giải

\(\frac{{ - 1}}{3}\;\) là số hữu tỉ nên \(\frac{{ - 1}}{3}\; \in Q\).

Đáp án B.

Câu 2. Số đối của \(\frac{{ - 8}}{9}\) là số nào?

Phương pháp

Dựa vào khái niệm số đối.

Lời giải

Số đối của \(\frac{{ - 8}}{9}\) là \(\frac{8}{9}\).

Đáp án D.

Câu 3.  Hãy sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn: \(\,\frac{{ - 15}}{{ - 17}};\,0;\,\frac{{25}}{{17}}; - \frac{3}{{17}}\)  ?

Phương pháp

So sánh lần lượt các cặp số hữu tỉ với nhau.

Lời giải

Ta có: \( - \frac{3}{{17}} < 0\) nên \( - \frac{3}{{17}}\) là số bé nhất.

\(\,\frac{{ - 15}}{{ - 17}} = \frac{{15}}{{17}} > \,0\).

So sánh \(\frac{{25}}{{17}}\) với \(\frac{{15}}{{17}}\): Vì 25 > 15 nên \(\frac{{25}}{{17}}\) > \(\frac{{15}}{{17}} = \frac{{ - 15}}{{ - 17}}\).

Vậy các số hữu tỉ sắp xếp theo thứ tự từ bé đến lớn là: \( - \frac{3}{{17}};0;\,\frac{{ - 15}}{{ - 17}};\frac{{25}}{{17}}\).

Đáp án C.

Câu 4. Quan sát trục số sau. Khẳng định nào sau đây đúng?

Phương pháp

Quan sát trục số để xác định các điểm trên trục số.

Lời giải

Quan sát trục số ta thấy mỗi ô là 1 đơn vị nên các điểm biểu diễn các số sau:

Điểm A biểu diễn số hữu tỉ \(\frac{1}{2}\).

Điểm B biểu diễn số hữu tỉ 1.

Điểm C biểu diễn số hữu tỉ \(\frac{{ - 7}}{2}\).

Vậy đáp án đúng là A.

Đáp án A.

Câu 5. Hình hộp chữ nhật có bao nhiêu cạnh?

Phương pháp

Dựa vào kiến thức về hình hộp chữ nhật.

Lời giải

Hình hộp chữ nhật có 4 cạnh bên và 8 cạnh đáy nên có 4 + 8 = 12 cạnh.

Đáp án D.

Câu 6. Ở mỗi đỉnh của hình lập phương có bao nhiêu góc?

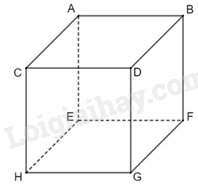
Phương pháp

Vẽ 1 hình lập phương và quan sát các góc ở mỗi đỉnh.

Lời giải

Đỉnh A có 3 góc vuông : góc CAE, góc BAE và góc BAC. Tương tự với các đỉnh khác.

Đáp án B.

Câu 7. Đường chéo của hình hộp chữ nhật \(ABCD.A'B'C'D'\) là đường nào?

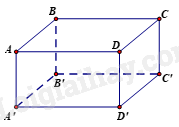
Phương pháp

Quan sát hình vẽ để tìm các đường chéo của hình hộp.

Lời giải

Các đường chéo của hình hộp chữ nhật ABCD.A’B’C’D’ là: AC’, BD’, CA’, DB’.

Đáp án C.

Câu 8. Hình hộp chữ nhật \(ABCD.A'B'C'D'\)có \(BC = 7\,{\rm{cm}}\). Khẳng định nào sau đây sai?

Phương pháp

Xác định các cạnh có độ dài bằng cạnh BC.

Lời giải

Các cạnh bằng cạnh BC là: AD, A’D’, B’C’.

Đáp án D.

Câu 9. Trong các hình sau, hình nào là hình lăng trụ đứng tam giác

Phương pháp

Dựa vào đặc điểm của hình lăng trụ đứng tam giác.

Lời giải

Trong các hình trên, chỉ có hình 3 là hình lăng trụ đứng tam giác.

Đáp án C.

Câu 10. Cho hình lăng trụ đứng tứ giác \(MNPQ.EFGH\) có cạnh \(ME = 7\,{\rm{cm}}\),\(HG = 4\,{\rm{cm}}\). Khẳng định nào sau đây đúng?

Phương pháp

Xác định các cạnh bằng nhau.

Lời giải

NF = ME = 7cm nên A đúng, B sai.

EH và NP chưa đủ điều kiện để xác định.

Đáp án A.

Câu 11. Các mặt bên của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là những hình gì?

Phương pháp

Dựa vào đặc điểm của hình lăng trụ đứng tứ giác.

Lời giải

Các mặt bên của hình lăng trụ đứng tam giác là hình chữ nhật (vì có 2 cặp cạnh đối bằng nhau và các góc là góc vuông).

Đáp án C.

Câu 12. Cho hình lăng trụ đứng tam giác như hình bên. Mặt đáy của lăng trụ đứng là:     

Phương pháp

Quan sát hình vẽ.

Lời giải

Hai mặt đáy của hình lăng trụ đứng tam giác trên là ABC và MNP.

Đáp án A.

Phần tự luận.

Bài 1. (0,75 điểm). Trong các số 2,5; 0; \( - \frac{1}{3}\), \(1\frac{1}{2}\) số nào là số hữu tỉ dương? Vì sao?

Phương pháp

So sánh các số hữu tỉ với 0.

Lời giải

Vì \(2,5 = \frac{{25}}{{10}} = \frac{5}{2} > 0\); \(1\frac{1}{2} = \frac{3}{2} > 0\) nên 2,5; \(1\frac{1}{2}\)  là các số hữu tỉ dương.

Bài 2. (1,5 điểm). Thực hiện phép tính:

Phương pháp

Dựa vào quy tắc tính với số hữu tỉ, lũy thừa.

Lời giải

a. \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\)\( = \frac{2}{3}.\frac{{ - 9}}{6} + \frac{1}{7}\)\( =  - 1 + \frac{1}{7}\)\( = \frac{{ - 6}}{7}\).

b. \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\)\( = \frac{{ - 3}}{{11}} \cdot \left( {\frac{5}{9} + \frac{4}{9}} \right)\)\( = \frac{{ - 3}}{{11}}.1\)\( = \frac{{ - 3}}{{11}}\).

c. \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\)\( = \frac{{{{\left( {{3^2}} \right)}^5}.{{\left( {{2^3}} \right)}^2}}}{{{{\left( {{3^3}} \right)}^3}{{.2}^4}}}\)\( = \frac{{{3^{10}}{{.2}^6}}}{{{3^9}{{.2}^4}}}\)\( = {3.2^2} = 3.4 = 12\).

Bài 3. (1,5 điểm).  Tìm số hữu tỉ \(x\), biết:

Phương pháp

Dựa vào quy tắc tính để tìm x.

Lời giải

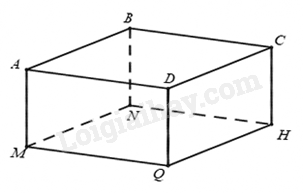
Bài 4. (1,0 điểm). Cho hình hộp chữ nhật ABCD.MNHQ như hình vẽ, có AB = 5cm, BC = 7cm, AM = 3cm Tính diện tích xung quanh và thể tích của hình hộp chữ nhật này.

Phương pháp

Dựa vào công thức tính diện tích xung quanh và thể tích của hình hộp chữ nhật.

Lời giải

Diện tích xung quanh của hình hộp chữ nhật là:

\({S_{xq}} = 2.\left( {5 + 7} \right).3 = 72\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).

Thể tích của hình hộp chữ nhật là:

\(V = 5.7.3 = 105\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)

Vậy diện tích xung quanh của hình hộp chữ nhật là 72cm².

            thể tích của hình hộp chữ nhật là 105cm³.

Bài 5. (0,75 điểm).

Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác. Hãy tính thể tích của thùng.

Phương pháp

Dựa vào công thức tính thể tích hình lăng trụ đứng tam giác.

Lời giải

Diện tích đáy hình lăng trụ đứng tam giác là:

\({S_d} = \frac{{90.60}}{2} = 2700\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).

Thể tích hình lăng trụ đứng tam giác là:

\(V = 2700.70 = 189000\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)

Vậy thể tích thùng đựng máy cắt cỏ là 189 00 cm³.

Bài 6. (0,5 điểm).  Một căn phòng hình hộp chữ nhật có chiều dài \(4,5m\), chiều rộng \(4m\) , chiều cao \(3m\).  Người ta muốn lăn sơn trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là  \(11\,{m^2}\). Tính diện tích cần lăn sơn ?

Phương pháp

Tính diện tích xung quanh của căn phòng.

Diện tích cần lăn sơn = diện tích xung quanh của căn phòng – diện tích các cửa.

Lời giải

Diện tích xung quanh căn phòng và diện tích trần nhà:

\(S = 2(4,5 + 4).3 + 4,5.4 = 69\left( {{{\rm{m}}^2}} \right)\).

Diện tích cần lăn sơn:

69 – 11 = 58 (m²)

Bài 7. (1,0 điểm). Một cửa hàng bán quần áo có chương trình khuyến mãi như sau: Khách hàng có thẻ thành viên sẽ được giảm 15% tổng số tiền của hóa đơn. Bạn Bình có thẻ thành viên, bạn mua hai chiếc áo sơ mi, mỗi áo đều có giá 200 000 đồng và một quần Jeans với giá 350 000 đồng. Bạn đưa cho người thu ngân 1 triệu đồng. Hỏi bạn Bình được trả lại bao nhiêu tiền?

Phương pháp

Tính số tiền Bạn bình phải trả.

Số tiền Bình được trả lại = số tiền Bình đưa – số tiền Bình phải trả.

Lời giải

Số tiền bạn Bình mua hai chiếc áo sơ mi và một quần Jeans sau khi giảm giá:

\((100\%  - 15\% ).(2.200000 + 350000) = 637500\)(đồng).

Số tiền Bình được trả lại:

1000000 – 637500 = 362500 (đồng).