Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 17Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Trong các khẳng định sau, khẳng định đúng là:
Câu 2 :
Căn bậc hai số học của 121 là:
Câu 3 :
Diện tích của đất nước Việt Nam là \(331690k{m^2}\). Làm tròn số này với độ chính xác là \(d = 500\) được số
Câu 4 :
Cho hình lăng trụ đứng tam giác ABC.DEF như hình vẽ. Biết AB = 4cm, AC = 3cm, BE = 6cm. Thể tích hình lăng trụ đó bằng
Câu 5 :
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 45^\circ \), số đo \(\widehat {yOz}\) bằng:
Câu 7 :
Nếu \(MN//a\) và \(MK//a\) thì theo tiên đề Euclid, ta có:
Câu 8 :
Nếu \(a//b\) và \(b \bot c\) thì
Câu 9 :
Trong các dữ liệu sau, dữ liệu nào là dữ liệu định tính?
Câu 10 :
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê chọn môn thể thao ưa thích nhất trong bốn môn: Bóng đá, Cầu lông, Bóng bàn, Bóng chuyền của học sinh khối 7 ở trường A. Mỗi học sinh chỉ được chọn một môn thể thao khi được hỏi ý kiến. Môn Thể thao được các bạn ưa thích nhất là:
Câu 11 :
Biểu đồ hình quạt tròn bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn món ăn ưa thích nhất trong bốn loại: Phở, Cơm, Gà rán, Bánh bao của học sinh khối 7. Mỗi học sinh chỉ chọn một kết quả khi hỏi ý kiến. Tỉ lệ ưa thích món Bánh bao của học sinh khối 7 chiếm bao nhiêu phần trăm?
Câu 12 :
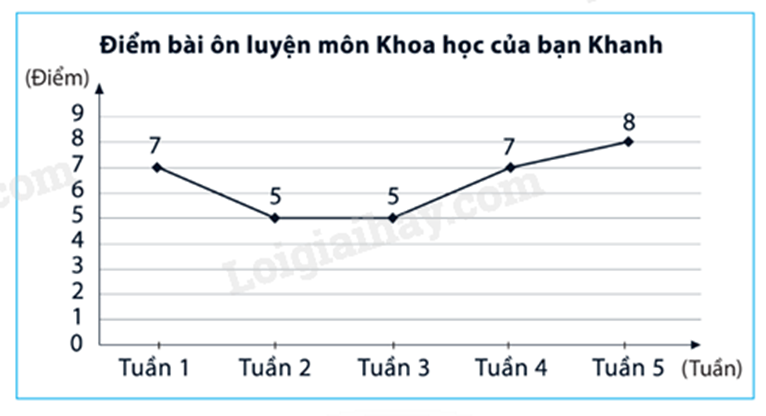
Biểu đồ đoạn thẳng trong hình bên biểu diễn điểm bài ôn luyện môn Khoa học của bạn Khanh qua các tuần 1, tuần 2, tuần 3, tuần 4, tuần 5. Hãy cho biết điểm 7 bạn Khanh đạt được vào tuần nào?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Trong các khẳng định sau, khẳng định đúng là:
Đáp án : A Phương pháp giải :
Kiểm tra xem các số có thuộc tập hợp số đó hay không. \(\mathbb{N}\) là tập hợp số tự nhiên. \(\mathbb{Z}\) là tập hợp số nguyên. \(\mathbb{Q}\) là tập hợp số hữu tỉ. Lời giải chi tiết :
\(3\) là số hữu tỉ nên \(3 \in \mathbb{Q}\) là khẳng định đúng. \(1\frac{1}{5} = \frac{6}{5}\) là số hữu tỉ nên \(1\frac{1}{5} \notin \mathbb{Q}\) là khẳng định sai. \(\frac{2}{3}\) không phải số tự nhiên nên \(\frac{2}{3} \in \mathbb{N}\) là khẳng định sai. \( - \frac{1}{7}\) không phải số nguyên nên \( - \frac{1}{7} \in \mathbb{Z}\) là khẳng định sai. Đáp án A
Câu 2 :
Căn bậc hai số học của 121 là:
Đáp án : B Phương pháp giải :
Áp dụng kiến thức về căn bậc hai của một số: \(x = {a^2}\) thì \(\sqrt x = a\) Lời giải chi tiết :
Căn bậc hai số học của 121 là: \(\sqrt {121} = 11\). Đáp án B
Câu 3 :
Diện tích của đất nước Việt Nam là \(331690k{m^2}\). Làm tròn số này với độ chính xác là \(d = 500\) được số
Đáp án : B Phương pháp giải :
Áp dụng quy tắc làm tròn số: Với độ chính xác là d = 500, ta làm tròn số đến hàng nghìn. Lời giải chi tiết :
Vì 690 > 500 nên 331 690 làm tròn với độ chính xác d = 500 là 332 000. Đáp án B
Câu 4 :
Cho hình lăng trụ đứng tam giác ABC.DEF như hình vẽ. Biết AB = 4cm, AC = 3cm, BE = 6cm. Thể tích hình lăng trụ đó bằng
Đáp án : B Phương pháp giải :
Thể tích hình lăng trụ là: \(V = S.h\) (S là diện tích đáy, h là chiều cao) Lời giải chi tiết :
Diện tích đáy của hình lăng trụ là: \(S = \frac{1}{2}.3.4 = 6\left( {c{m^2}} \right)\) Thể tích hình lăng trụ là: \(V = S.h = 6.6 = 36\left( {c{m^3}} \right)\). Đáp án B
Câu 5 :
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 45^\circ \), số đo \(\widehat {yOz}\) bằng:
Đáp án : D Phương pháp giải :
Tổng hai góc kề bù bằng \(180^\circ \). Lời giải chi tiết :
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) \(\begin{array}{l}45^\circ + \widehat {yOz} = 180^\circ \\\widehat {yOz} = 180^\circ - 45^\circ \\\widehat {yOz} = 135^\circ \end{array}\) Đáp án D
Đáp án : B Phương pháp giải :
Áp dụng tính chất hai góc đối đỉnh bằng nhau. Lời giải chi tiết :
Vì \(\widehat {{A_2}}\) và \(\widehat {{A_3}}\) là hai góc đối đỉnh nên ta có: \(\widehat {{A_3}} = \widehat {{A_2}} = 68^\circ \). Đáp án B
Câu 7 :
Nếu \(MN//a\) và \(MK//a\) thì theo tiên đề Euclid, ta có:
Đáp án : C Phương pháp giải :
Theo tiên đề Euclid, qua một điểm nằm ngoài một đường thẳng, ta chỉ có thể kẻ được 1 đường thẳng song song với đường đó. Lời giải chi tiết :
Nếu \(MN//a\) và \(MK//a\) thì MN trùng với MK (vì qua điểm M ta chỉ có một đường thẳng song song với a) Do đó M, N, K cùng nằm trên một đường thẳng. Đáp án C
Câu 8 :
Nếu \(a//b\) và \(b \bot c\) thì
Đáp án : B Phương pháp giải :
Nếu đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại. Lời giải chi tiết :
Nếu \(a//b\) và \(b \bot c\) thì \(a \bot c\). Đáp án B
Câu 9 :
Trong các dữ liệu sau, dữ liệu nào là dữ liệu định tính?
Đáp án : A Phương pháp giải :
Phân loại dữ liệu: Dữ liệu là số còn gọi là dữ liệu định lượng Dữ liệu là không là số còn gọi là dữ liệu định tính. Lời giải chi tiết :
Dữ liệu định tính là: Các loại nước giải khát: nước suối, nước chanh, trà sữa,… vì dữ liệu không là số. Đáp án A
Câu 10 :
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê chọn môn thể thao ưa thích nhất trong bốn môn: Bóng đá, Cầu lông, Bóng bàn, Bóng chuyền của học sinh khối 7 ở trường A. Mỗi học sinh chỉ được chọn một môn thể thao khi được hỏi ý kiến. Môn Thể thao được các bạn ưa thích nhất là:
Đáp án : A Phương pháp giải :
Môn thể thao có tỉ số phần trăm lớn nhất là môn có nhiều bạn ưu thích nhất. Lời giải chi tiết :
Môn Thể thao được các bạn ưu thích nhất là Bóng đá (40%). Đáp án A
Câu 11 :
Biểu đồ hình quạt tròn bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn món ăn ưa thích nhất trong bốn loại: Phở, Cơm, Gà rán, Bánh bao của học sinh khối 7. Mỗi học sinh chỉ chọn một kết quả khi hỏi ý kiến. Tỉ lệ ưa thích món Bánh bao của học sinh khối 7 chiếm bao nhiêu phần trăm?
Đáp án : C Phương pháp giải :
Tỉ lệ ưa thích món Bánh bao của học sinh khối 7 = 100% - tổng số phần trăm học sinh ưu thích các món còn lại. Lời giải chi tiết :
Tỉ lệ ưa thích món Bánh bao của học sinh khối 7 chiếm: 100% - 15% - 5% - 26% = 54% Đáp án C
Câu 12 :
Biểu đồ đoạn thẳng trong hình bên biểu diễn điểm bài ôn luyện môn Khoa học của bạn Khanh qua các tuần 1, tuần 2, tuần 3, tuần 4, tuần 5. Hãy cho biết điểm 7 bạn Khanh đạt được vào tuần nào?
Đáp án : B Phương pháp giải :
Quan sát biểu đồ xác định các tuần có điểm là 7. Lời giải chi tiết :
Bạn Khanh đạt được điểm 7 vào tuần 1 và tuần 4. Đáp án B
II. Tự luận
Phương pháp giải :
a) Sử dụng quy tắc cộng và nhân số hữu tỉ. b) Để làm tròn số thực âm, ta sẽ làm tròn số đối của nó rồi thêm dấu “ –“ vào trước kết quả làm tròn. Lời giải chi tiết :
a) Ta có: \(\frac{2}{3} + \left( { - \frac{3}{2}} \right).\left( { - \frac{4}{{10}}} \right) = \frac{2}{3} + \left( { - \frac{3}{2}} \right).\left( { - \frac{2}{5}} \right) = \frac{2}{3} + \frac{3}{5} = \frac{{19}}{{15}}\) b) Làm tròn số \( - 4,3615\) với độ chính xác d = 0,05, ta được \( - 4,4\). Phương pháp giải :
Áp dụng quy tắc chuyển vế đổi dấu. b) Nếu \(\left| A \right| = 0\) thì A = 0. Lời giải chi tiết :
a) \(\frac{4}{9} - \frac{2}{3}.x = \frac{1}{3}\) \(\begin{array}{l}\frac{2}{3}x = \frac{4}{9} - \frac{1}{3}\\\frac{2}{3}x = \frac{1}{9}\\x = \frac{1}{9}:\frac{2}{3}\\x = \frac{1}{6}\end{array}\) Vậy \(x = \frac{1}{6}\) b) \(\left| {x + \frac{1}{2}} \right| = 0\) \(\begin{array}{l}x + \frac{1}{2} = 0\\x = 0 - \frac{1}{2}\\x = - \frac{1}{2}\end{array}\) Vậy \(x = - \frac{1}{2}\) Phương pháp giải :
a) Phân loại dữ liệu: Dữ liệu là số còn gọi là dữ liệu định lượng Dữ liệu là không là số còn gọi là dữ liệu định tính. b) Tính tổng số học sinh. Tính m% của a theo công thức: m%.a để tính tỉ lệ phần trăm học sinh. Lời giải chi tiết :
a) Dữ liệu định tính là tình trạng: Bơi thành thạo, Biết bơi nhưng chưa thành thạo, Chưa biết bơi. Dữ liệu định lượng là số học sinh: 250; 175; 75. b) Tổng số học sinh là: 250 + 175 + 75 = 500 (học sinh) Tỉ số phần trăm học sinh bơi thành thạo là: \(\frac{{250}}{{500}} = 100\% = 50\% \) Tỉ số phần trăm học sinh biết bơi nhưng chưa thành thạo là: \(\frac{{175}}{{500}}.100\% = 35\% \) Tỉ số phần trăm học sinh chưa biết bơi là: \(\frac{{75}}{{500}}.100\% = 15\% \) Phương pháp giải :
1. Sử dụng công thức tính diện tích xung quanh của hình hộp chữ nhật: Sxq = chu vi đáy. chiều cao. 2. a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại. b) Áp dụng tính chất hai đường thẳng song song có hai góc đồng vị bằng nhau và hai góc đối đỉnh. c) Hai góc kề bù có tổng bằng \(180^\circ \) nên ta tính được góc mBA. Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau. Lời giải chi tiết :
1. Diện tích xung quanh của hộp quà là: Sxq = 2.(10 + 8).12 = 432 (cm2). Vậy diện tích xung quanh của hộp quà là 432cm2. 2. a) Vì \(xy//mn\), \(xy \bot d\) nên \(mn \bot d\). b) Vì \(xy//mn\) nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (hai góc đồng vị) nên \(\widehat {{B_1}} = 60^\circ \). Vì \(\widehat {{B_1}} = \widehat {{B_2}}\) (hai góc đối đỉnh) nên \(\widehat {{B_2}} = 60^\circ \). c) Vì \(\widehat {mBA}\) và \(\widehat {{B_1}}\) là hai góc kề bù nên \(\widehat {mBA} + \widehat {{B_1}} = 180^\circ \), suy ra \(\widehat {mBA} = 180^\circ - \widehat {{B_1}} = 180^\circ - 60^\circ = 120^\circ \). Vì BK là tia phân giác của góc mBA nên \(\widehat {mBK} = \frac{1}{2}\widehat {mBA} = \frac{1}{2}.120^\circ = 60^\circ \). Phương pháp giải :
Tính khối lượng cặp sách của bạn Đức khi biết cân nặng và tỉ số phần trăm khối lượng cặp sách so với cân nặng. Từ đó tính khối lượng vở mới bạn Đức có thể mang nhiều nhất = khối lượng cặp sách – khối lượng chiếc cặp. Tính số quyển vở tương ứng với \(\frac{4}{{25}}kg\). Lời giải chi tiết :
Theo khuyến nghị, khối lượng cặp sách bạn Đức nên mang không vượt quá là: 46 . 10% = 4,6 (kg). Khối lượng vở mới Đức có thể mang thêm nhiều nhất theo khuyến nghị là: 4,6 – 3,5 = 1,1 (kg). 1,1kg ứng với số quyển vở nặng \(\frac{4}{{25}}\)kg là: \(1,1:\frac{4}{{25}} = 1,1.\frac{{25}}{4} = 6,875\) Do đó bạn Đức có thể mang theo nhiều nhất 6 quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên.
|























Danh sách bình luận