Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 9Phần trắc nghiệm (3 điểm) Câu 1: Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được:Đề bài
I. Trắc nghiệm
Câu 1 :
Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được:
Câu 2 :
Biết \(\frac{x}{2} = \frac{y}{3}\) và \(x + y = - 15\). Khi đó giá trị của x, y là
Câu 3 :
Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:
Giá trị cần điền vào “?” là
Câu 4 :
Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi \(x = - 2\) thì \(y = 4\). Khi đó, hệ số a bằng bao nhiêu?
Câu 5 :
Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
Câu 8 :
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
Câu 9 :
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
Câu 10 :
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
Câu 11 :
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
Câu 12 :
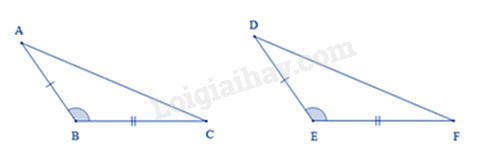
Hai tam giác bằng nhau là
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được:
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về tỉ lệ thức. Lời giải chi tiết :
Ta có: \(1,2:1,35 = \frac{{1,2}}{{1,35}} = \frac{8}{9} = 8:9\).
Câu 2 :
Biết \(\frac{x}{2} = \frac{y}{3}\) và \(x + y = - 15\). Khi đó giá trị của x, y là
Đáp án : D Phương pháp giải :
Dựa vào tính chất dãy tỉ số bằng nhau. Lời giải chi tiết :
Ta có: \(\frac{x}{2} = \frac{y}{3} = \frac{{x + y}}{{2 + 3}} = \frac{{ - 15}}{5} = - 3\) (tính chất dãy tỉ số bằng nhau) Suy ra \(x = - 3.2 = - 6;y = - 3.3 = - 9\).
Câu 3 :
Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:
Giá trị cần điền vào “?” là
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận. Lời giải chi tiết :
Vì y tỉ lệ thuận với x nên \(k = \frac{y}{x} = \frac{{ - 5}}{1} = - 5 = \frac{1}{?}\) suy ra \(? = 1:\left( { - 5} \right) = \frac{{ - 1}}{5}\).
Câu 4 :
Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi \(x = - 2\) thì \(y = 4\). Khi đó, hệ số a bằng bao nhiêu?
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch. Lời giải chi tiết :
Vì y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên \(a = xy = \left( { - 2} \right).4 = - 8\).
Câu 5 :
Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
Đáp án : B Phương pháp giải :
Dựa vào quan hệ giữa ba cạnh của một tam giác. Lời giải chi tiết :
Ta có: 5 – 4 = 1 nên 5cm; 4cm; 1cm không thể tạo thành một tam giác. 3cm; 4cm; 5cm có thể tạo thành một tam giác nên ta chọn đáp án B. 2 + 2 = 4 < 5 nên 5cm; 2cm; 2cm không thể tạo thành một tam giác. 1 + 4 = 5 < 10 nên 1cm; 4cm; 10cm không thể tạo thành một tam giác.
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về hai tam giác bằng nhau. Lời giải chi tiết :
Xét tam giác ABC và tam giác DEF có: \(\begin{array}{l}AB = DE\\\widehat {ABC} = \widehat {DEF}\\BC = EF\end{array}\) Suy ra \(\Delta ABC = \Delta DEF\) (cạnh – góc – cạnh)
Đáp án : D Phương pháp giải :
Dựa vào tính chất của tam giác cân và hai góc kề bù. Lời giải chi tiết :
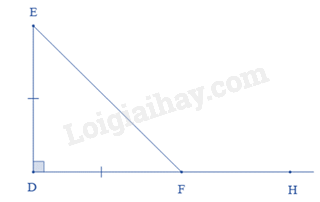
Tam giác DEF có \(\widehat D = {90^0}\) và DE = DF nên tam giác DEF vuông cân tại D. Suy ra \(\widehat {DEF} = \widehat {DFE} = \frac{{{{180}^0} - {{90}^0}}}{2} = {45^0}\). Ta có \(\widehat {DFE} + \widehat {EFH} = {180^0}\) (hai góc kề bù) Suy ra \(\widehat {EFH} = {180^0} - \widehat {DFE} = {180^0} - {45^0} = {135^0}\).
Câu 8 :
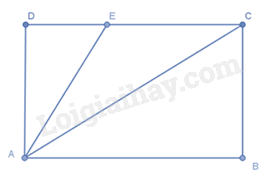
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
Đáp án : A Phương pháp giải :
Dựa vào quan hệ giữa đường xiên và hình chiếu. Lời giải chi tiết :
Xét tam giác vuông ACD có AD < AC (trong tam giác vuông, cạnh huyền là cạnh lớn nhất) Vì E nằm trên cạnh CD nên DE < DC suy ra AE < AC (quan hệ giữa đường vuông góc và đường xiên. Suy ra AD < AE < AC nên A sai.
Câu 9 :
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
Đáp án : D Phương pháp giải :
Dựa vào khái niệm về đường trung trực của đoạn thẳng. Lời giải chi tiết :
“Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó”.
Câu 10 :
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận. Lời giải chi tiết :
Vì y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2 nên \(y = 2x\). Thay \(x = - 3\) vào công thức ta được: \(y = 2.\left( { - 3} \right) = - 6\).
Câu 11 :
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch. Lời giải chi tiết :
Vì hai đại lượng x và y là hai đại lượng tỉ lệ nghịch với nhau nên \(a = - 12.8 = - 96\). Thay \(x = 3\) vào công thức ta được: \( - 96 = 3.y\) suy ra \(y = - 32\).
Câu 12 :
Hai tam giác bằng nhau là
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về hai tam giác bằng nhau. Lời giải chi tiết :
Hai tam giác bằng nhau là hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau.
II. Tự luận
Phương pháp giải :
Áp dụng tính chất của tỉ lệ thức. Lời giải chi tiết :
a) Ta có: \(\frac{{ - 6}}{x} = \frac{9}{{ - 15}}\) Suy ra \(\left( { - 6} \right).\left( { - 15} \right) = 9.x\) \(x = \frac{{\left( { - 6} \right).\left( { - 15} \right)}}{9} = 10\) Vậy x = 10. b) Ta có: \(\frac{{ - 4}}{x} = \frac{x}{{ - 49}}\) Suy ra \(\left( { - 4} \right)\left( { - 49} \right) = x.x\) \(\begin{array}{l}{x^2} = 196\\x = \pm 14\end{array}\) Vậy \(x = \pm 14\). Phương pháp giải :
Áp dụng tính chất của dãy tỉ số bằng nhau. Lời giải chi tiết :
a) Ta có: \(\frac{a}{b} = \frac{6}{5}\) suy ra \(\frac{a}{6} = \frac{b}{5}\). Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{a}{6} = \frac{b}{5} = \frac{{a - b}}{{6 - 5}} = \frac{3}{1} = 3\). Suy ra \(a = 3.6 = 18\); \(b = 3.5 = 15\). Vậy a = 16; b = 15. b) Ta có: \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5} = \frac{{x - y + z}}{{2 - 3 + 5}} = \frac{{32}}{4} = 8\). Suy ra \(x = 8.2 = 16\) \(\begin{array}{l}y = 8.3 = 24\\z = 8.5 = 40\end{array}\) Vậy \(x = 16;y = 24;z = 40\). Phương pháp giải :
Dựa vào tính chất của dãy tỉ số bằng nhau. Lời giải chi tiết :
Gọi x, y, z (tấn)lần lượt là khối lượng hàng các đơn vị A, B, C vận chuyển (x, y, z > 0). Theo đề bài ta suy ra: \(\frac{x}{{50}} = \frac{y}{{80}} = \frac{z}{{70}}\) và \(x + y + z = 700\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\begin{array}{l}\frac{x}{{50}} = \frac{y}{{80}} = \frac{z}{{70}} = \frac{{x + y + z}}{{50 + 80 + 70}} = \frac{{700}}{{200}} = 3,5\\x = 175;\quad y = 280;\quad z = 245\end{array}\) Vậy khối lượng hàng các đơn vị A, B, C vận chuyển lần lượt là 175; 280; 245 tấn. Phương pháp giải :
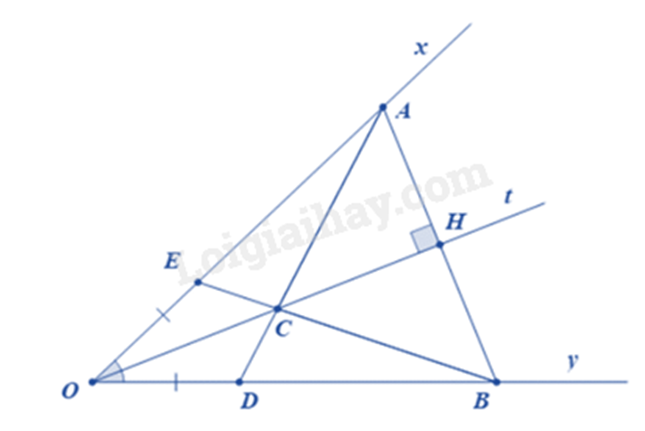
a) Chứng minh được: ∆AHO = ∆BHO (góc – cạnh – góc) Suy ra OA = OB (hai cạnh tương ứng) b) Chứng minh được: ∆AHC = ∆BHC (hai cạnh góc vuông) Suy ra \(\widehat {ACH} = \widehat {HCB}\) (hai góc tương ứng) c) Chứng minh được: ∆OEC = ∆ODC (c.g.c) Chứng minh được: \(\widehat {ECO} + \widehat {OCD} + \widehat {BCD} = {180^0}\) Suy ra ba điểm E, C, B thẳng hàng. Lời giải chi tiết :
a) Xét tam giác AHO và tam giác BHO có: \(\widehat {AOH} = \widehat {BOH}\) (Ot là tia phân giác của \(\widehat {AOB}\)) OH chung \(\widehat {AHO} = \widehat {BHO}\left( { = {{90}^0}} \right)\) Suy ra \(\Delta AHO = \Delta BHO\left( {g.c.g} \right)\) Suy ra OA = OB (hai cạnh tương ứng) (đpcm) b) \(\Delta AHO = \Delta BHO\) suy ra AH = HB (hai cạnh tương ứng) Xét tam giác AHC và tam giác BHC có: HC chung \(\widehat {AHC} = \widehat {BHC}\left( { = {{90}^0}} \right)\) AH = HB Suy ra \(\Delta AHC = \Delta BHC\) (hai cạnh góc vuông) Suy ra \(\widehat {ACH} = \widehat {HCB}\) (hai góc tương ứng) c) Xét tam giác OCE và OCD có: OE = OD \(\widehat {EOC} = \widehat {DOC}\) OC chung Suy ra ∆OEC = ∆ODC (c.g.c) Suy ra EC = DC (hai cạnh tương ứng) Ta có OA = OB và OE = OD nên AE = BD. Xét \(\Delta ECA\) và \(\Delta DCB\) có: EC = ED (cmt) EA = DB (cmt) CA = CB (\(\Delta AHC = \Delta BHC\)) Suy ra \(\Delta ECA = \Delta DCB\) (c.c.c) Suy ra \(\widehat {ECA} = \widehat {DCB}\) (hai góc tương ứng) Mặt khác \(\widehat {ECA} + \widehat {ECD} = {180^0}\) (vì AC cắt Oy tại D) Suy ra \(\widehat {DCB} + \widehat {ECD} = {180^0}\) hay B, C, E thẳng hàng (đpcm). Phương pháp giải :
Đặt \(\frac{a}{b} = \frac{c}{d} = k\). Áp dụng dãy tỉ số bằng nhau để chứng minh. Lời giải chi tiết :
Đặt \(\frac{a}{b} = \frac{c}{d} = k \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = bk}\\{c = dk}\end{array}} \right.\) Do đó ta có: \(\frac{{ac}}{{bd}} = \frac{{bkdk}}{{bd}} = {k^2}(1)\) Ta cũng có: \(\frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}} = \frac{{{{(bk)}^2} + {{(dk)}^2}}}{{{b^2} + {d^2}}} = \frac{{{b^2}{k^2} + {d^2}{k^2}}}{{{b^2} + {d^2}}} = \frac{{{k^2}\left( {{b^2} + {d^2}} \right)}}{{{b^2} + {d^2}}} = {k^2}(2)\) Từ (1) và (2) suy ra: \(\frac{{ac}}{{bd}} = \frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}} = \left( {{k^2}} \right)\) (đpcm)
|






















Danh sách bình luận