Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 10Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... Phần trắc nghiệm (3 điểm) Câu 1: Từ tỉ lệ thức $\frac{a}{b}=\frac{c}{d}$ (giả thiết các tỉ số đều có nghĩa) ta suy ra đẳng thức:Đề bài
I. Trắc nghiệm
Câu 1 :
Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) (giả thiết các tỉ số đều có nghĩa) ta suy ra đẳng thức:
Câu 2 :
Từ đẳng thức 2.12 = 8.3 ta có thể lập được bao nhiêu tỉ lệ thức?
Câu 3 :
Cho biết đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2. Hãy biểu diễn y theo x?
Câu 4 :
Cho biết đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 12. Hệ số tỉ lệ là:
Câu 5 :
Tổng số đo các góc của tam giác bằng
Câu 6 :
Cho \(\Delta MNP = \Delta LKQ\), MN = 3cm, MP = 4cm, NP = 5cm, \(\widehat M = {90^0}\). Khi đó:
Câu 7 :
Tam giác ABC có AB = 8cm, BC = 6cm, AC = 4cm. So sánh các góc của tam giác ta có:
Câu 8 :
Bộ ba độ dài nào sau đây là 3 cạnh của một tam giác?
Câu 10 :
Cho tam giác MNK có MN = NK. Khi đó:
Câu 11 :
Cho tam giác ABC cân tại C. Khi đó
Câu 12 :
Đường vuông góc kẻ từ điểm A đến đường thẳng m là
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) (giả thiết các tỉ số đều có nghĩa) ta suy ra đẳng thức:
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về tỉ lệ thức. Lời giải chi tiết :
Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) ta suy ra \(a.d = b.c\)
Câu 2 :
Từ đẳng thức 2.12 = 8.3 ta có thể lập được bao nhiêu tỉ lệ thức?
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về tỉ lệ thức. Lời giải chi tiết :
Từ đẳng thức 2.12 = 8.3 ta có thể lập được 4 tỉ lệ thức là: \(\frac{2}{3} = \frac{8}{{12}};\frac{2}{8} = \frac{3}{{12}};\frac{3}{2} = \frac{{12}}{8};\frac{8}{2} = \frac{{12}}{3}\).
Câu 3 :
Cho biết đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2. Hãy biểu diễn y theo x?
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận. Lời giải chi tiết :
Vì đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2 nên ta có công thức \(y = 2x\).
Câu 4 :
Cho biết đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 12. Hệ số tỉ lệ là:
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch. Lời giải chi tiết :
Vì y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên \(a = xy = 2.12 = 24\).
Câu 5 :
Tổng số đo các góc của tam giác bằng
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về tổng ba góc của một tam giác. Lời giải chi tiết :
Tổng số đo các góc của tam giác là \({180^0}\).
Câu 6 :
Cho \(\Delta MNP = \Delta LKQ\), MN = 3cm, MP = 4cm, NP = 5cm, \(\widehat M = {90^0}\). Khi đó:
Đáp án : A Phương pháp giải :
Dựa vào đặc điểm của hai tam giác bằng nhau. Lời giải chi tiết :
Ta có \(\Delta MNP = \Delta LKQ\) suy ra \(MN = KL = 3cm;\widehat M = \widehat L = {90^0}\) suy ra đáp án A đúng.
Câu 7 :
Tam giác ABC có AB = 8cm, BC = 6cm, AC = 4cm. So sánh các góc của tam giác ta có:
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa góc và cạnh đối diện trong tam giác để so sánh. Lời giải chi tiết :
Trong tam giác ABC có AC < BC < AB (4cm > 6cm > 8cm) suy ra \(\widehat B < \widehat A < \widehat C\).
Câu 8 :
Bộ ba độ dài nào sau đây là 3 cạnh của một tam giác?
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa ba cạnh của một tam giác. Lời giải chi tiết :
Ta có 3 + 4 = 7 < 8 nên 3cm, 4cm, 8cm không thể là ba cạnh của một tam giác. Ta có 3 + 7 = 10 nên 10cm, 7cm, 3cm không thể là ba cạnh của một tam giác. Ta có 4 + 5 = 9 nên 9cm, 5cm, 4cm không thể là ba cạnh của một tam giác. Vậy chỉ có 6cm, 7cm, 10cm là ba cạnh của một tam giác.
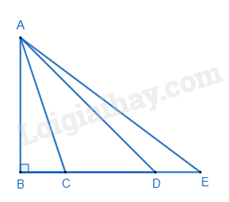
Đáp án : A Phương pháp giải :
Dựa vào mối quan hệ giữa đường vuông góc và đường xiên. Lời giải chi tiết :
Vì AB là đường vuông góc kẻ từ A xuống BE nên AB nhỏ nhất. Quan sát hình vẽ ta thấy C nằm giữa B và D nên BC < BD suy ra AC < AD. Mà D lại nằm giữa B và E nên BD < BE suy ra AD < AE. Suy ra AB < AC < AD < AE.
Câu 10 :
Cho tam giác MNK có MN = NK. Khi đó:
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về tam giác cân. Lời giải chi tiết :
Tam giác MNK có MN = NK là tam giác cân tại N.
Câu 11 :
Cho tam giác ABC cân tại C. Khi đó
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về tam giác cân. Lời giải chi tiết :
Tam giác ABC cân tại C nên \(\widehat A = \widehat B\).
Câu 12 :
Đường vuông góc kẻ từ điểm A đến đường thẳng m là
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về đường vuông góc. Lời giải chi tiết :
Đường vuông góc kẻ từ điểm A đến đường thẳng m là đường thẳng kẻ từ A đến m và vuông góc với m.
II. Tự luận
Phương pháp giải :
Áp dụng tính chất của tỉ lệ thức. Lời giải chi tiết :
a) Ta có: \(\frac{x}{6} = \frac{4}{3}\) Suy ra \(x.3 = 4.6\) \(x = \frac{{4.6}}{3} = 8\) Vậy x = 8. b) Ta có: \(7:x = - 9:4\) Suy ra \(\frac{7}{x} = \frac{{ - 9}}{4}\) \(\begin{array}{l}7.4 = - 9.x\\x = \frac{{7.4}}{{ - 9}} = \frac{{ - 28}}{9}\end{array}\) Vậy \(x = \frac{{ - 28}}{9}\). Phương pháp giải :
Áp dụng tính chất của dãy tỉ số bằng nhau. Lời giải chi tiết :
Gọi số học sinh giỏi của ba lớp 7A, 7B, 7C lần lượt là a, b, c. \(\left( {a,b,c \in \mathbb{N}*} \right)\) Vì số học sinh giỏi của ba lớp 7A, 7B, 7C lần lượt tỉ lệ với 4; 3; 2 nên ta có: \(\frac{a}{4} = \frac{b}{3} = \frac{c}{2}\). Vì tổng số học sinh giỏi của cả ba lớp là 45 em ta có a + b + c = 45. Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\frac{a}{4} = \frac{b}{3} = \frac{c}{2} = \frac{{a + b + c}}{{4 + 3 + 2}} = \frac{{45}}{9} = 5\) Suy ra \(a = 5.4 = 20\) \(\begin{array}{l}b = 5.3 = 15\\c = 5.2 = 10\end{array}\) Vậy số học sinh giỏi của lớp 7A, 7B, 7C lần lượt là 20; 15; 10 học sinh. Phương pháp giải :
Sử dụng hệ quả của bất đẳng thức tam giác. Lời giải chi tiết :
Theo đề bài AC = 30km, AB = 90km suy ra AC < AB. Trong ∆ABC có: CB > AB – AC (hệ quả của bất đẳng thức tam giác) Suy ra CB > 90 – 30 = 60km Vậy nếu đặt tại C máy phát sóng truyền thanh có bán kính hoạt động bằng 60km thì thành phố B không nhận được tín hiệu. Phương pháp giải :
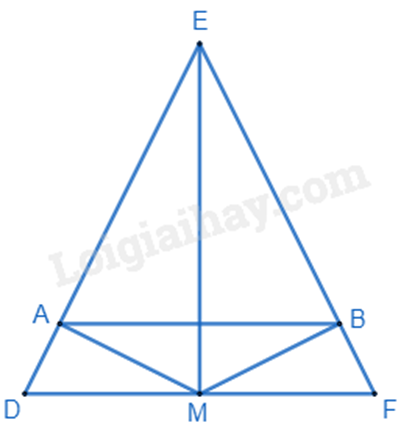
a) Chứng minh \(\Delta EDM{\rm{ }} = {\rm{ }}\Delta EFM\) theo trường hợp cạnh – cạnh – cạnh. b) Chứng minh \(\widehat {EMD} = \widehat {EMF} = {90^0}\) suy ra \(EM \bot DF\). c) Chứng minh \(\Delta EAB\) cân nên \(\widehat {EAB} = \widehat {EDF}\), mà hai góc ở vị trí đồng vị nên AB // DF. Lời giải chi tiết :
a) Xét \(\Delta EDM\) và \(\Delta EFM\) có: DE = EF (tam giác DFE cân tại E) DM = MF (M là trung điểm của DF) ME chung Suy ra \(\Delta EDM = \Delta EFM\) (c.c.c) (đpcm) b) \(\Delta EDM = \Delta EFM\) suy ra \(\widehat {EMD} = \widehat {EMF}\) (hai góc tương ứng) Mà \(\widehat {EMD}\) và \(\widehat {EMF}\) là hai góc kề bù nên \(\widehat {EMD} + \widehat {EMF} = {180^0}\) Suy ra \(\widehat {EMD} = \widehat {EMF} = \frac{{{{180}^0}}}{2} = {90^0}\) hay \(EM \bot DF\) (đpcm) c) \(\Delta EDM = \Delta EFM\) suy ra \(\widehat {DEM} = \widehat {FEM}\) (hai góc tương ứng) Xét \(\Delta AEM\) và \(\Delta BEM\) có: \(\widehat {AEM} = \widehat {BEM}\) (cmt) \(\widehat {EAM} = \widehat {EBM}\left( { = {{90}^0}} \right)\) EM chung Suy ra \(\Delta AEM = \Delta BEM\) (cạnh huyền – góc nhọn) Suy ra AE = EB (hai cạnh tương ứng) suy ra \(\Delta AEB\) là tam giác cân tại E. \(\widehat {EAB} = \widehat {EBA} = \frac{{{{180}^0} - \widehat E}}{2}\) Mà \(\Delta DFE\) cân tại E nên \(\widehat {EDF} = \widehat {EFD} = \frac{{{{180}^0} - \widehat E}}{2}\) Suy ra \(\widehat {EAB} = \widehat {EDF}\). Mà \(\widehat {EAB}\) và \(\widehat {EDF}\) là hai góc đồng vị nên AB // DF (đpcm) Phương pháp giải :
Biến đổi \(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}\) thành \(\frac{{a + b}}{{ab}} = \frac{{b + c}}{{bc}} = \frac{{a + c}}{{ac}}\) và rút gọn để tìm a, b, c. Thay a, b, c vào M để tính giá trị của M. Lời giải chi tiết :
Ta có:\(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ac}}{{a + c}}\) \(\frac{{a + b}}{{ab}} = \frac{{b + c}}{{bc}} = \frac{{a + c}}{{ac}}\) \(\frac{a}{{ab}} + \frac{b}{{ab}} = \frac{b}{{bc}} + \frac{c}{{bc}} = \frac{a}{{ac}} + \frac{c}{{ac}}\) suy ra \(\frac{1}{a} + \frac{1}{b} = \frac{1}{b} + \frac{1}{c} = \frac{1}{a} + \frac{1}{c}\) Ta có \(\frac{1}{a} + \frac{1}{b} = \frac{1}{b} + \frac{1}{c}\) \(\frac{1}{a} = \frac{1}{c}\) suy ra \(a = c\) (1) \(\frac{1}{b} + \frac{1}{c} = \frac{1}{a} + \frac{1}{c}\) \(\frac{1}{a} = \frac{1}{b}\) suy ra \(a = b\) (2) Từ (1) và (2) suy ra a = b = c Thay vào M, ta được: \(\begin{array}{l}M = \frac{{2ab + 3bc + ca}}{{2{a^2} + 3{b^2} + {c^2}}}\\M = \frac{{2.a.a + 3.a.a + a.a}}{{2{a^2} + 3{a^2} + {a^2}}}\\M = \frac{{6{a^2}}}{{6{a^2}}} = 1\end{array}\) Vậy M = 1.
|
