Đề thi giữa kì 1 Toán 7 - Đề số 7Tải về Phần trắc nghiệm (3 điểm) Câu 1. Tập hợp các số hữu tỉ kí hiệu là: Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Phần trắc nghiệm (3 điểm) Câu 1. Tập hợp các số hữu tỉ kí hiệu là: A. N. B. \({N*}\). C. Q . D. Z . Câu 2. Số đối cùa \(\frac{{ - 2}}{3}\) là: A. \(\frac{2}{3}\). B. \(\frac{3}{2}\). C. \(\frac{{ - 3}}{2}\). D. \(\frac{2}{{ - 3}}\). Câu 3. Giá trị của \({\left( {{x^m}} \right)^n}\) bằng: A. \({x^{m + n}}\). B. \({x^{m.n}}\). C. \({x^{m:n}}\) . D. \({x^m}^{ - n}\).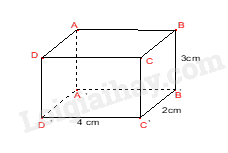 
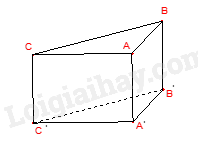
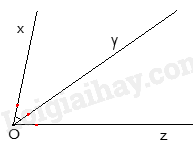
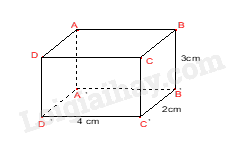
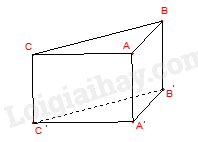
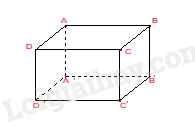
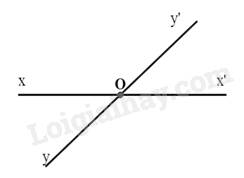
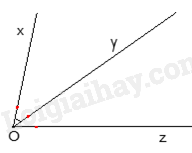
Câu 4. Số mặt của hình hộp chữ nhật \(ABCD.A'B'C'D'\) là: A. 3. B. 4. C. 5. D. 6. Câu 5. Thể tích của hình hộp chữ nhật bên là: A. 6. B. 8. C. 12. D. 24. Câu 6. Cho hình lăng trụ đứng tam giác \(ABC.A'B'C'\) các mặt bên của hình trên là những hình gì? A. Tam giác. B. Tứ giác. C. Hình chữ nhật. D. Hình vuông. Câu 7. Số đỉnh của hình hộp chữ nhật là: A. 6. B. 8. C. 10. D. 12. Câu 8. Cho một hình lăng trụ đứng có diện tích đáy là S, chiều cao là h. Hỏi công thức tính thể tích của hình lăng trụ đứng là gì? A. V = S.h. B. V = \(\frac{1}{2}S.h\). C. V = 2S.h. D. V = 3S.h. Câu 9. Hai đường thẳng xx’ và yy’ cắt nhau tại O. Góc đối đỉnh của góc \(\widehat {xOy}'\) là: A. \(\widehat {x'Oy}'\). B. \(\widehat {x'Oy}\). C. \(\widehat {xOy}\). D. \(\widehat {y'Ox}\). Câu 10. Cho hình vẽ, biết \(\widehat {xOy} = {40^0}\), Oy là tia phân giác của góc \(\widehat {xOz}\). Khi đó số đo \(\widehat {yOz}\) bằng:
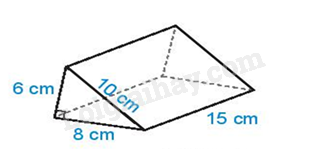
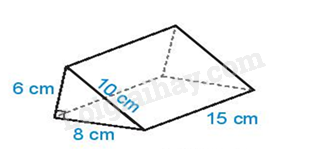
A. 200. B. 1400. C. 800. D. 400. Câu 11. Kết quả của phép tính \({2^2}{.2^5}\) là: A. 210. B. 23. C. 25. D. 27. Câu 12. Kết quả của phép tính \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là: A. \(\frac{{ - 1}}{{35}}\). B. \(\frac{{ - 17}}{{60}}\). C. \(\frac{{ - 5}}{{35}}\). D. \(\frac{{ - 1}}{{60}}\). Phần tự luận (7 điểm) Bài 1. (1,75 điểm). Tính: a. \(\frac{7}{6} - \frac{1}{6}:\frac{2}{3}\); b. \(13,3\,.\,45\; - \;44\,.\,13,3\); c. \(2021 - {\left( {\frac{1}{3}} \right)^2}{.3^2}\). Bài 2. (1,0 điểm). Tìm x biết: a. \(2x - \frac{1}{3} = \frac{5}{3}\); b. \({\left( {2x + 3} \right)^2} = 25\); Bài 3. (1,5 điểm). Tính diện tích xung quanh và thể tích hình lăng trụ đứng trong hình sau:
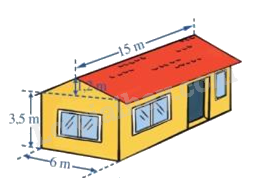
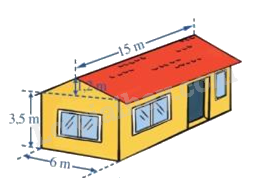
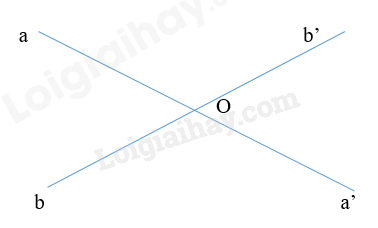
Bài 4. (1,25 điểm). Một ngôi nhà có cấu trúc và kích thước như hình sau. Tính thể tích phần không gian được giới hạn bởi ngôi nhà đó. Bài 5. (1 điểm). Cho đường thẳng aa’ cắt bb’ tại O. a. Kể tên các cặp góc đối đỉnh b. Kể tên các cặp góc kề bù c. Dùng dụng cụ học tập để vẽ tia phân giác của góc aOb. -------- Hết -------- Lời giải Phần trắc nghiệm (3 điểm)
Câu 1. Tập hợp các số hữu tỉ kí hiệu là:
Phương pháp Dựa vào khái niệm các tập hợp đã học. Lời giải Tập hợp các số hữu tỉ kí hiệu là Q. Đáp án C. Câu 2. Số đối cùa \(\frac{{ - 2}}{3}\) là:
Phương pháp Dựa vào khái niệm số đối. Lời giải Số đối của \(\frac{{ - 2}}{3}\) là \(\frac{2}{3}\). Đáp án A. Câu 3. Giá trị của \({\left( {{x^m}} \right)^n}\) bằng:
Phương pháp Dựa vào cách tính lũy thừa của lũy thừa. Lời giải \({\left( {{x^m}} \right)^n}\) = \({x^{m.n}}\). Đáp án B. Câu 4. Số mặt của hình hộp chữ nhật \(ABCD.A'B'C'D'\) là:
Phương pháp Quan sát hình vẽ. Lời giải Hình hộp chữ nhật có 6 mặt. Đáp án D. Câu 5. Thể tích của hình hộp chữ nhật bên là:
Phương pháp Dựa vào công thức tính thể tích hình hộp chữ nhật. Lời giải Thể tích hình hộp chữ nhật bên là: \(V = 3.4.2 = 24\). Đáp án D. Câu 6. Cho hình lăng trụ đứng tam giác \(ABC.A'B'C'\) các mặt bên của hình trên là những hình gì?
Phương pháp Quan sát hình bên. Lời giải Các mặt bên của hình lăng trụ đứng tam giác \(ABC.A'B'C'\) là: ABB’A’, ACC’A’, BCC’B’. Các hình này là hình chữ nhật. Đáp án C. Câu 7. Số đỉnh của hình hộp chữ nhật là:
Phương pháp Dựa vào kiến thức về hình hộp chữ nhật hoặc vẽ một hình hộp chữ nhật để xác định. Lời giải
Hình hộp chữ nhật có 8 đỉnh. Đáp án B. Câu 8. Cho một hình lăng trụ đứng có diện tích đáy là S, chiều cao là h. Hỏi công thức tính thể tích của hình lăng trụ đứng là gì?
Phương pháp Kiến thức về tính thể tích hình lăng trụ đứng. Lời giải V = S.h. Đáp án A. Câu 9. Hai đường thẳng xx’ và yy’ cắt nhau tại O. Góc đối đỉnh của góc \(\widehat {xOy}'\) là:
Phương pháp Vẽ đường thẳng xx’ và yy’ cắt nhau tại O và xác định góc đối đỉnh của \(\widehat {xOy}'\) trong hình vẽ. Lời giải Quan sát hình vẽ ta thấy góc đối đỉnh của \(\widehat {xOy}'\) là \(\widehat {x'Oy}\). Đáp án B. Câu 10. Cho hình vẽ, biết \(\widehat {xOy} = {40^0}\), Oy là tia phân giác của góc \(\widehat {xOz}\). Khi đó số đo \(\widehat {yOz}\) bằng:
Phương pháp Vì Oy là tia phân giác nên ta có cặp góc bằng nhau. Lời giải Vì Oy là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {xOy} = \widehat {yOz}\). Mà \(\widehat {xOy} = {40^0}\) nên \(\widehat {yOz} = {40^0}\). Đáp án D. Câu 11. Kết quả của phép tính \({2^2}{.2^5}\) là:
Phương pháp Dựa vào quy tắc nhân hai lũy thừa cùng cơ số. Lời giải Ta có: \({2^2}{.2^5} = {2^{2 + 5}} = {2^7}\). Đáp án D. Câu 12. Kết quả của phép tính \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là:
Phương pháp Dựa vào quy tắc cộng số hữu tỉ. Lời giải \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}} = \frac{{ - 3.3}}{{60}} + \frac{{ - 2.4}}{{60}} = \frac{{ - 9 - 8}}{{60}} = \frac{{ - 17}}{{60}}\). Đáp án B.
Phần tự luận. Bài 1. (1,75 điểm). Tính:
Phương pháp Dựa vào quy tắc tính với số hữu tỉ, lũy thừa. Lời giải a. \(\frac{7}{6} - \frac{1}{6}:\frac{2}{3}\) = \(\frac{7}{6} - \frac{1}{6}.\frac{3}{2} = \frac{7}{6} - \frac{1}{4} = \frac{{14}}{{12}} - \frac{3}{{12}} = \frac{{11}}{{12}}\). b. 13,3 . 45 – 44 . 13,3 = 13,3 . (45 – 44) = 13,3 . 1 = 13,3. c. \(2021 - {\left( {\frac{1}{3}} \right)^2}{.3^2}\) = 2021 - \(\frac{1}{{{3^2}}}\;.\;{3^2}\) = 2020. Bài 2. (1,0 điểm). Tìm x biết:
Phương pháp Dựa vào quy tắc tính để tìm x. Lời giải a. 2x – \(\frac{1}{3} = \frac{5}{3}\) \(\Leftrightarrow\) 2x = \(\frac{5}{3} + \frac{1}{3}\) \(\Leftrightarrow\) 2x = 2 \(\Leftrightarrow\) x = 1. b. (2x + 3)2 = 25 \( \Leftrightarrow \left[ \begin{array}{l}2x + 3 = 5\\2x + 3 = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 4\end{array} \right.\). Bài 3. (1,5 điểm). Tính diện tích xung quanh và thể tích hình lăng trụ đứng trong hình sau: Phương pháp Dựa vào quy tắc tính diện tích xung quanh và thể tích của hình lăng trụ đứng. Lời giải Diện tích xung quanh hình lăng trụ đứng là : Sxq = Cđáy . h = (6 + 10 + 8) .15 = 360 (m2 ) Diện tích một đáy của hình lăng trụ là : Sđáy = \(\frac{{6.8}}{2}\) = 24 (m2 ) Thể tích của hình lăng trụ đứng là V = Sđáy . h = 24.15 = 360 ( m3) Bài 4. (1,25 điểm). Một ngôi nhà có cấu trúc và kích thước như hình sau. Tính thể tích phần không gian được giới hạn bởi ngôi nhà đó.
Phương pháp Dựa vào công thức tính thể tích của hình hộp chữ nhật và hình lăng trụ tam giác. Thể tích phần không gian được giới hạn bởi ngôi nhà = thể tích phần hình lăng trụ tam giác + thể tích phần hình lăng trụ hình hộp chữ nhật. Lời giải Thể tích phần không gian có dạng hình lăng trụ tam giác là: V1 = (6.1,2:2) . 15= 54 (m3) Thể tích phần không gian có dạng hình hộp chữ nhật là: V2 = 15.6.3,5 = 315 (m3) Thể tích phần không gian được giới hạn bởi ngôi nhà đó là: V = V1 + V2 = 54 + 315 = 369 (m3) Bài 5. (1 điểm). Cho đường thẳng aa’ cắt bb’ tại O. a. Kể tên các cặp góc đối đỉnh b. Kể tên các cặp góc kề bù Phương pháp Dựa vào kiến thức về góc đối đỉnh, góc kề bù. Lời giải a) Các cặp góc đối đỉnh: \(\widehat {aOb}\) và \(\widehat {a'Ob'}\); \(\widehat {aOb'}\) và \(\widehat {a'Ob}\). b) Các cặp góc kề bù: \(\widehat {aOb}\) và \(\widehat {aOb'}\); \(\widehat {aOb}\) và \(\widehat {a'Ob}\); \(\widehat {a'Ob'}\) và \(\widehat {aOb'}\); \(\widehat {a'Ob'}\) và \(\widehat {a'Ob}\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
