Đề thi giữa kì 1 Toán 7 - Đề số 5Tải vềI. TRẮC NGHIỆM ( 3 điểm) Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài I. TRẮC NGHIỆM ( 3 điểm) Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng. Câu 1: Lớp 7B có \(\dfrac{4}{5}\) số học sinh thích học toán, \(\dfrac{7}{{10}}\) số học sinh thích học văn, \(\dfrac{{23}}{{25}}\) số học sinh thích học Tiếng Anh. Môn học nào được nhiều bạn học sinh lớp 7B yêu thích nhất? A. Môn toán B. Môn văn C. Môn Tiếng Anh D. Môn toán và môn văn Câu 2: Kết quả của phép tính: \(\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{{23}} - \dfrac{1}{6}\) A. \(\dfrac{1}{{23}}\) B. \(\dfrac{{26}}{{69}}\) C. \(\dfrac{3}{{23}}\) D. \(\dfrac{2}{{23}}\) Câu 3: Kết quả của phép tính: \({2^{23}}:{4^3}\) là: A. \({2^{17}}\) B. \({2^{26}}\) C. \({2^{29}}\) D. \({2^{20}}\) Câu 4: Diện tích xung quanh của hình lập phương biết độ dài một bằng \(3a\). A. \(9{a^2}\) B. \(27{a^2}\) C. \(32{a^2}\) D. \(36{a^2}\) Câu 5: Cho \(\angle xBy = {60^0}\). Vẽ góc đối đỉnh với \(\angle xBy\). Hỏi góc này có số đo bằng bao nhiêu độ? A. \({30^0}\) B. \({60^0}\) C. \({90^0}\) D. \({120^0}\) Câu 6: Tính thể tích hộp sữa có dạng hình hộp chữ nhật như hình vẽ bên dưới:
A. \(1000\,c{m^3}\) B. \(1500\,c{m^3}\) C. \(1000\,c{m^2}\) D. \(1500\,c{m^2}\)
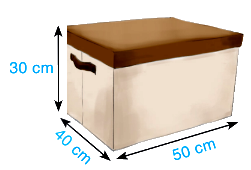
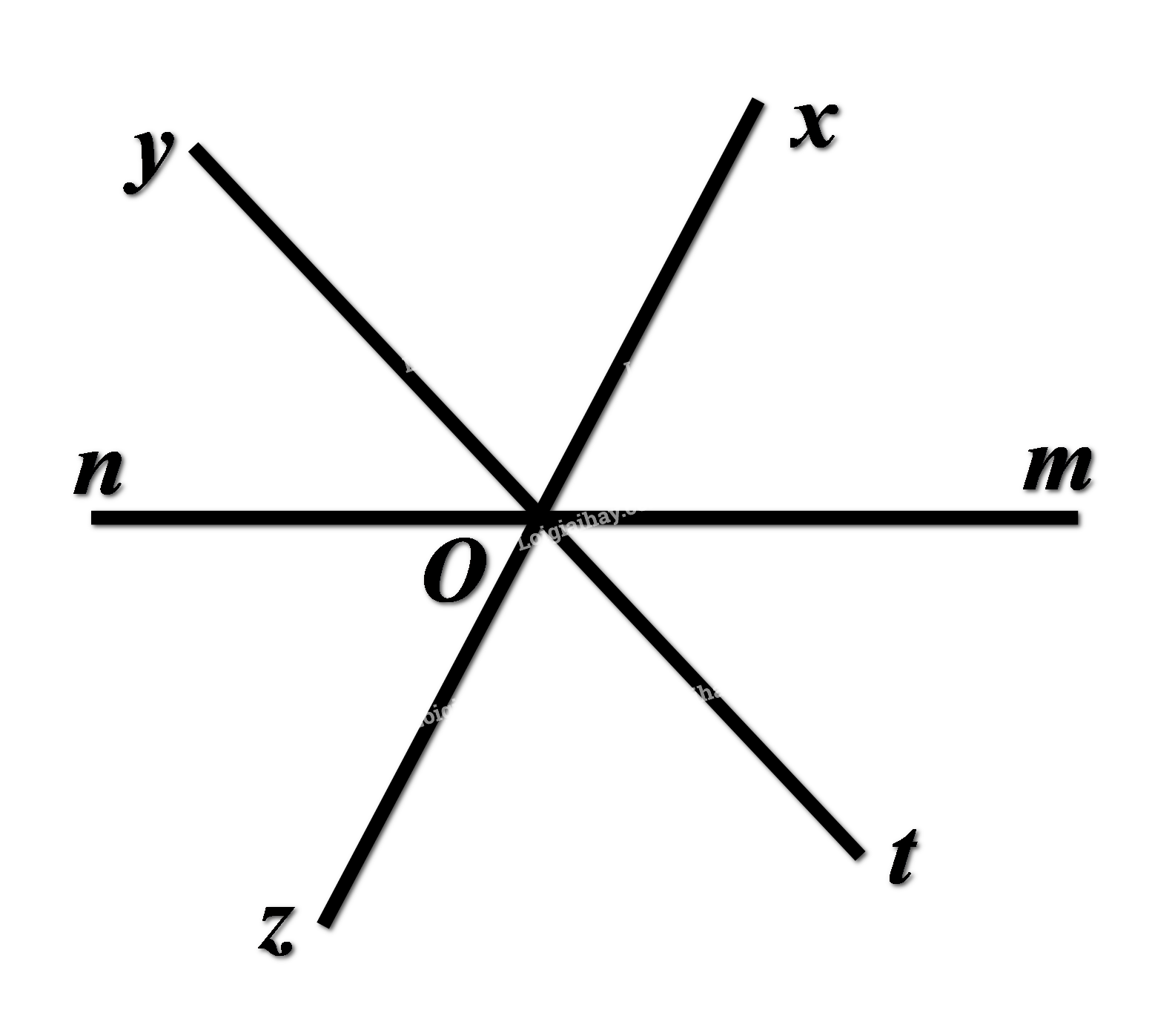
Phần II. Tự luận (7 điểm): Bài 1: (2,0 điểm) Thực hiện phép tính: a) \(\dfrac{{ - 4}}{7} - \dfrac{5}{{13}}.\dfrac{{ - 39}}{{25}} + \dfrac{{ - 1}}{{42}}:\left( { - \dfrac{5}{6}} \right)\) b) \(\left( {\dfrac{4}{5} + \dfrac{{ - 9}}{7}} \right):\dfrac{{2025}}{{2030}} + \left( {\dfrac{{ - 5}}{7} - \dfrac{{ - 6}}{5}} \right):\dfrac{{2025}}{{2030}}\) c) \({\left( {{3^2}} \right)^2} - {\left( { - {2^3}} \right)^2} - {\left( { - {5^2}} \right)^2}\) d) \({2^3} + 3.{\left( {\dfrac{1}{2}} \right)^0}.{\left( {\dfrac{1}{2}} \right)^2}.4 + \left[ {{{\left( { - 2} \right)}^2}:\dfrac{1}{2}} \right]:8\) Bài 2: (1,0 điềm) So sánh: a) \(5\) và \(\sqrt {16} \) b) \(\sqrt {9.16} \) và \(\sqrt 9 .\sqrt {16} \). c) \(\sqrt 7 + \sqrt {15} \) và \(7\) d) \(\sqrt {50} - \sqrt 2 \) và \(\sqrt {50 - 2} \) Bài 3: (2,0 điểm) Tìm \(x\), biết: a) \(\left( {2x + \dfrac{5}{3}} \right).\left( {\dfrac{5}{4} - x} \right) = 0\) b) \(\dfrac{3}{5}x + \left( {x + 0,5} \right) = \dfrac{{ - 13}}{{15}}\) c) \({3^x} + {3^{x + 2}} = {9^{17}} + {27^{12}}\) d) \(\dfrac{1}{2}{.2^x} + {4.2^x} = {9.2^5}\) Bài 4: (1,0 điểm) Một chiếc hộp đựng đồ đa năng có dạng hình hộp chữ nhật với khung bằng thép, bên ngoài phủ vải và có kích thước như hình vẽ bên dưới: a) Tính thể tích của hộp. b) Người ta chọn vải có giá 15000 đồng cho \(0,5{m^2}\) vải. Hãy tính số tiền chi trả khi phủ bề ngoài của chiếc hộp. Bài 5: (1,0 điểm) Cho \(\angle xOy\). Vẽ \(\angle yOz\) kề bù với \(\angle xOy\). Vẽ \(\angle xOt\) kề bù với \(\angle xOy\). Vẽ \(On\) là tia phân giác \(\angle yOz\). Vẽ \(Om\) là phân giác của \(\angle xOt\). Khi đó \(\angle zOn\) và \(\angle xOm\) có phải là hai góc đối đỉnh hay không? Lời giải Phần I: Trắc nghiệm:
Câu 1: Phương pháp: Thực hiện so sánh các số hữu tỉ. Cách giải: Ta có: \(\dfrac{4}{5} = \dfrac{{40}}{{50}}\,\,;\,\,\dfrac{7}{{10}} = \dfrac{{35}}{{50}}\,\,;\,\,\dfrac{{23}}{{50}} = \dfrac{{46}}{{50}}\) Vì \(35 < 40 < 46\) nên \(\dfrac{{35}}{{50}} < \dfrac{{40}}{{50}} < \dfrac{{46}}{{50}}\) do đó, \(\dfrac{7}{{10}} < \dfrac{4}{5} < \dfrac{{23}}{{25}}\) Suy ra \(\dfrac{{23}}{{25}}\) là số hữu tỉ lớn nhất. Vậy môn Tiếng Anh được nhiều bạn học sinh lớp 7B yêu thích nhất. Chọn A. Câu 2: Phương pháp: Thực hiện phép cộng, trừ các số hữu tỉ. Cách giải: \(\begin{array}{l}\,\,\,\,\,\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{{23}} - \dfrac{1}{6}\\ = \left( {\dfrac{1}{2} - \dfrac{1}{3} - \dfrac{1}{6}} \right) + \dfrac{1}{{23}}\\ = \left( {\dfrac{3}{6} - \dfrac{2}{6} - \dfrac{1}{6}} \right) + \dfrac{1}{{23}}\\ = \dfrac{0}{6} + \dfrac{1}{{23}} = 0 + \dfrac{1}{{23}}\\ = \dfrac{1}{{23}}\end{array}\) Chọn A. Câu 3: Phương pháp: Áp dụng công thức tính thương của hai lũy thừa cùng cơ số: Với \(x \in \mathbb{Q},m,n \in \mathbb{N}\) ta có: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\). Cách giải: Ta có: \({2^{23}}:{4^3}\)\( = {2^{23}}:{\left( {{2^2}} \right)^3} = {2^{23}}:{2^6} = {2^{23 - 6}} = {2^{17}}\) Chọn A. Câu 4: Phương pháp: Diện tích xung quanh của hình lập phương có độ dài một cạnh bằng \(x\) được tính theo công thức: \(V = 4{x^2}\) Cách giải: Diện tích xung quanh của hình lập phương là: \({S_{xq}} = 4.{\left( {3a} \right)^2} = 4.9{a^2} = 36{a^2}\) Chọn D. Câu 5: Phương pháp: Hai góc đối đỉnh thì bằng nhau. Cách giải: Gọi \(\angle x'By'\) là góc đối đỉnh của \(\angle xBy\) suy ra \(\angle x'By' = \angle xBy = {60^0}\) (Hai góc đối đỉnh thì bằng nhau) Chọn B. Câu 6: Phương pháp: Thể tích hình hộp chữ nhật có dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c\) được tính theo công thức: \(V = abc\) Cách giải: Thể tích hộp sữa hình hộp chữ nhật là: \(V = 10.10.15 = 1\,500\,\left( {c{m^3}} \right)\) Chọn B. Phần II. Tự luận: Bài 1: Phương pháp: Thực hiện các phép tính cộng, trừ, nhân và chia với các số hữu tỉ. Áp dụng công thức tính lũy thừa: \({\left( {{a^m}} \right)^n} = {a^{m.n}};\,{\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\) Cách giải: a) \(\dfrac{{ - 4}}{7} - \dfrac{5}{{13}}.\dfrac{{ - 39}}{{25}} + \dfrac{{ - 1}}{{42}}:\left( { - \dfrac{5}{6}} \right)\) \(\begin{array}{l} = \dfrac{{ - 4}}{7} - \dfrac{5}{{13}}.\dfrac{{\left( { - 3} \right).13}}{{5.5}} + \dfrac{{ - 1}}{{6.7}}.\dfrac{{\left( { - 6} \right)}}{5}\\ = \dfrac{{ - 4}}{7} - \dfrac{{ - 3}}{5} + \dfrac{1}{{35}}\\ = \dfrac{{ - 20}}{{35}} - \dfrac{{ - 21}}{{35}} + \dfrac{1}{{35}}\\ = \dfrac{{ - 20 - \left( { - 21} \right) + 1}}{{35}}\\ = \dfrac{2}{{35}}\end{array}\) b) \(\left( {\dfrac{4}{5} + \dfrac{{ - 9}}{7}} \right):\dfrac{{2025}}{{2030}} + \left( {\dfrac{{ - 5}}{7} - \dfrac{{ - 6}}{5}} \right):\dfrac{{2025}}{{2030}}\) \(\begin{array}{l} = \left( {\dfrac{4}{5} + \dfrac{{ - 9}}{7}} \right).\dfrac{{2030}}{{2025}} + \left( {\dfrac{{ - 5}}{7} - \dfrac{{ - 6}}{5}} \right).\dfrac{{2030}}{{2025}}\\ = \left( {\dfrac{4}{5} + \dfrac{{ - 9}}{7} + \dfrac{{ - 5}}{7} - \dfrac{{ - 6}}{5}} \right).\dfrac{{2030}}{{2025}}\\ = \left[ {\left( {\dfrac{4}{5} - \dfrac{{ - 6}}{5}} \right) + \left( {\dfrac{{ - 9}}{7} + \dfrac{{ - 5}}{7}} \right)} \right].\dfrac{{2030}}{{2025}}\\ = \left( {\dfrac{{10}}{5} + \dfrac{{ - 14}}{7}} \right).\dfrac{{2030}}{{2025}}\\ = \left[ {2 + \left( { - 2} \right)} \right].\dfrac{{2030}}{{2025}}\\ = 0.\dfrac{{2030}}{{2025}}\\ = 0\end{array}\) c) \({\left( {{3^2}} \right)^2} - {\left( { - {2^3}} \right)^2} - {\left( { - {5^2}} \right)^2}\) \(\begin{array}{l} = {3^4} - {\left( { - 2} \right)^6} - {\left( { - 5} \right)^4}\\ = 81 - 64 - 625\\ = - 608\end{array}\) d) \({2^3} + 3.{\left( {\dfrac{1}{2}} \right)^0}.{\left( {\dfrac{1}{2}} \right)^2}.4 + \left[ {{{\left( { - 2} \right)}^2}:\dfrac{1}{2}} \right]:8\) \(\begin{array}{l} = 8 + 3.1.\dfrac{1}{4}.4 + \left( {4.2} \right):8\\ = 8 + 3 + 8:8\\ = 8 + 3 + 1 = 12\end{array}\) Bài 2: Phương pháp: Tính giá trị các căn bậc hai rồi so sánh kết quả tìm được. Cách giải: a) \(5\) và \(\sqrt {16} \) Ta có: \(\sqrt {16} = \sqrt {{4^2}} = 4\) Vì \(4 < 5\) nên \(\sqrt {16} < 5\) Vậy \(\sqrt {16} < 5\) b) \(\sqrt {9.16} \) và \(\sqrt 9 .\sqrt {16} \). Ta có: \(\sqrt {9.16} = \sqrt {144} = 12\) \(\sqrt 9 .\sqrt {16} = 3.4 = 12\) Suy ra: \(\sqrt {9.16} = \sqrt 9 .\sqrt {16} \) Vậy \(\sqrt {9.16} = \sqrt 9 .\sqrt {16} \). c) \(\sqrt 7 + \sqrt {15} \) và \(7\) Vì \(7 < 9\) nên \(\sqrt 7 < \sqrt 9 = \sqrt {{3^2}} = 3\), suy ra \(\sqrt 7 < 3\) Vì \(15 < 16\) nên \(\sqrt {15} < \sqrt {16} = \sqrt {{4^2}} = 4\), suy ra \(\sqrt {15} < 4\) Do đó, ta suy ra được: \(\sqrt 7 + \sqrt {15} < 3 + 4 = 7\) Vậy \(\sqrt 7 + \sqrt {15} < 7\) d) \(\sqrt {50} - \sqrt 2 \) và \(\sqrt {50 - 2} \) + \(\sqrt {50} - \sqrt 2 \) Vì \(50 < 64\) nên \(\sqrt {50} < \sqrt {64} = \sqrt {{8^2}} = 8\) Vì \(2 < 4\) nên \(\sqrt 2 < \sqrt 4 = \sqrt {{2^2}} = 2\) Do đó, ta suy ra được: \(\sqrt {50} - \sqrt 2 < 8 - 2 = 6\) Vậy \(\sqrt {50} - \sqrt 2 < 6\) + \(\sqrt {50 - 2} = \sqrt {48} \) Vì \(48 > 36\) nên \(\sqrt {48} > \sqrt {36} = \sqrt {{6^2}} = 6\) Do đó, ta suy ra được: \(\sqrt {48} > 6\) Vậy \(\sqrt {50 - 2} > 6\) Ta có: \(\sqrt {50} - \sqrt 2 < 6\) \(\sqrt {50 - 2} > 6\) Suy ra \(\sqrt {50} - \sqrt 2 < \sqrt {50 - 2} \) Vậy \(\sqrt {50} - \sqrt 2 < \sqrt {50 - 2} \). Bài 3: Phương pháp: a) \(A\left( x \right).B\left( x \right) = 0\) Trường hợp 1: Giải \(A\left( x \right) = 0\) Trường hợp 2: Giải \(B\left( x \right) = 0\) b) Vận dụng quy tắc chuyển vế tìm \(x\). c), d) \({a^m} = {a^n}\) khi \(m = n\) Cách giải: a) \(\left( {2x + \dfrac{5}{3}} \right).\left( {\dfrac{5}{4} - x} \right) = 0\) Trường hợp 1: \(2x + \dfrac{5}{3} = 0\) \(\begin{array}{l}2x = \dfrac{{ - 5}}{3}\\x = \dfrac{{ - 5}}{3}:2 = \dfrac{{ - 5}}{3}.\dfrac{1}{2}\\x = \dfrac{{ - 5}}{6}\end{array}\) Trường hợp 2: \(\dfrac{5}{4} - x = 0\) \(\begin{array}{l} - x = \dfrac{{ - 5}}{4}\\x = \dfrac{5}{4}\end{array}\) Vậy \(x \in \left\{ {\dfrac{{ - 5}}{6};\dfrac{5}{4}} \right\}\) b) \(\dfrac{3}{5}x + \left( {x + 0,5} \right) = \dfrac{{ - 13}}{{15}}\) \(\begin{array}{l}\dfrac{3}{5}x + x + 0,5 = \dfrac{{ - 13}}{{15}}\\\left( {\dfrac{3}{5} + 1} \right).x + \dfrac{1}{2} = \dfrac{{ - 13}}{{15}}\\\left( {\dfrac{3}{5} + \dfrac{5}{5}} \right).x = \dfrac{{ - 13}}{{15}} - \dfrac{1}{2}\\\dfrac{8}{5}.x = \dfrac{{ - 26}}{{30}} - \dfrac{{15}}{{30}}\\\dfrac{8}{5}.x = \dfrac{{ - 11}}{{30}}\\x = \dfrac{{ - 11}}{{30}}:\dfrac{8}{5}\\x = \dfrac{{ - 11}}{{30}}.\dfrac{5}{8}\\x = \dfrac{{ - 11}}{{48}}\end{array}\) Vậy \(x = \dfrac{{ - 11}}{{48}}\) c) \({3^x} + {3^{x + 2}} = {9^{17}} + {27^{12}}\) \(\begin{array}{l}{3^x} + {3^x}{.3^2} = {\left( {{3^2}} \right)^{17}} + {\left( {{3^3}} \right)^{12}}\\{3^x}.\left( {1 + {3^2}} \right) = {3^{34}} + {3^{36}}\\{3^x}.\left( {1 + 9} \right) = {3^{34}} + {3^{34 + 2}}\\{3^x}.10 = {3^{34}} + {3^{34}}{.3^2}\\{3^x}.10 = {3^{34}}.\left( {1 + {3^2}} \right)\\{3^x}.10 = {3^{34}}.\left( {1 + 9} \right)\\{3^x}.10 = {3^{34}}.10\\{3^x} = {3^{34}}\\ \Rightarrow x = 34\end{array}\) Vậy \(x = 34\) d) \(\begin{array}{l}{2^x}.\left( {\dfrac{1}{2} + 4} \right) = {9.2^5}\\{2^x}.\left( {\dfrac{1}{2} + \dfrac{8}{2}} \right) = {9.2^5}\\{2^x}.\dfrac{9}{2} = {9.2^5}\\{2^x} = {9.2^5}:\dfrac{9}{2} = {9.2^5}.\dfrac{2}{9}\\{2^x} = {2^6}\\ \Rightarrow x = 6\end{array}\) Vậy \(x = 6\) Bài 4: Phương pháp: Hình hộp chữ nhật có dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c\) a) Thể tích hình hộp chữ nhật được tính theo công thức: \(V = abc\) b) Diện tích xung quanh của hình hộp chữ nhật tính theo công thức: \({S_{xq}} = 2\left( {a + b} \right).c\) Cách giải: a) Thể tích của hộp là: \(30.40.50 = 60\,000\) (đồng) b) \(1{m^2}\) vải có giá: \(15\,000.2 = 30\,000\) (đồng) Diện tích vải cần phủ là: \(2.\left( {40 + 50} \right).30 = 2.90.30 = 5\,400\,\left( {c{m^2}} \right) = 0,54\left( {{m^2}} \right)\) Số tiền cần phải chi trả là: \(0,54.30\,000 = 16\,200\) (đồng) Bài 5: Phương pháp: Chứng minh: + \(\angle nOz = \angle xOm\); + \(Om\) và \(On\) là hai tia đối nhau Cách giải: Vì \(\angle yOz\) kề bù với \(\angle xOy\) nên \(Ox\) và \(Oz\) là hai tia đối nhau \(\angle xOy\) kề bù với \(\angle xOt\) nên \(Oy\) và \(Ot\) là hai tia đối nhau. Ta có: \(\angle yOz = \angle xOt\) (hai góc đối đỉnh thì bằng nhau) Do \(On\) là đường phân giác của \(\angle yOz\)\( \Rightarrow \angle yOn = \angle nOz = \dfrac{1}{2}\angle yOz\) (tính chất đường phân giác của một góc) \(Om\) là đường phân giác của \(\angle xOt\) \( \Rightarrow \angle xOm = \angle mOt = \dfrac{1}{2}\angle xOt\) (tính chất đường phân giác của một góc) Suy ra \(\angle nOz = \angle xOm;\angle mOt = \angle yOn\) Lại có: \(\angle xOy\) và \(\angle xOt\) là hai góc kề bù nên \(\angle xOy + \angle xOt = {180^0}\) \(\begin{array}{l} \Rightarrow \angle xOy + \angle xOm + \angle mOt = {180^0}\\ \Rightarrow \angle xOy + \angle xOm + \angle yOn = {180^0}\\ \Rightarrow \left( {\angle xOy + \angle yOn} \right) + \angle xOm = {180^0}\\ \Rightarrow \angle xOn + \angle xOm = {180^0}\end{array}\) Suy ra \(\angle xOn\) và \(\angle xOm\) là hai góc kề bù. Do đó, \(Om\) và \(On\) là hai tia đối nhau Vậy \(\angle zOn\) và \(\angle xOm\) là hai góc đối đỉnh.
|















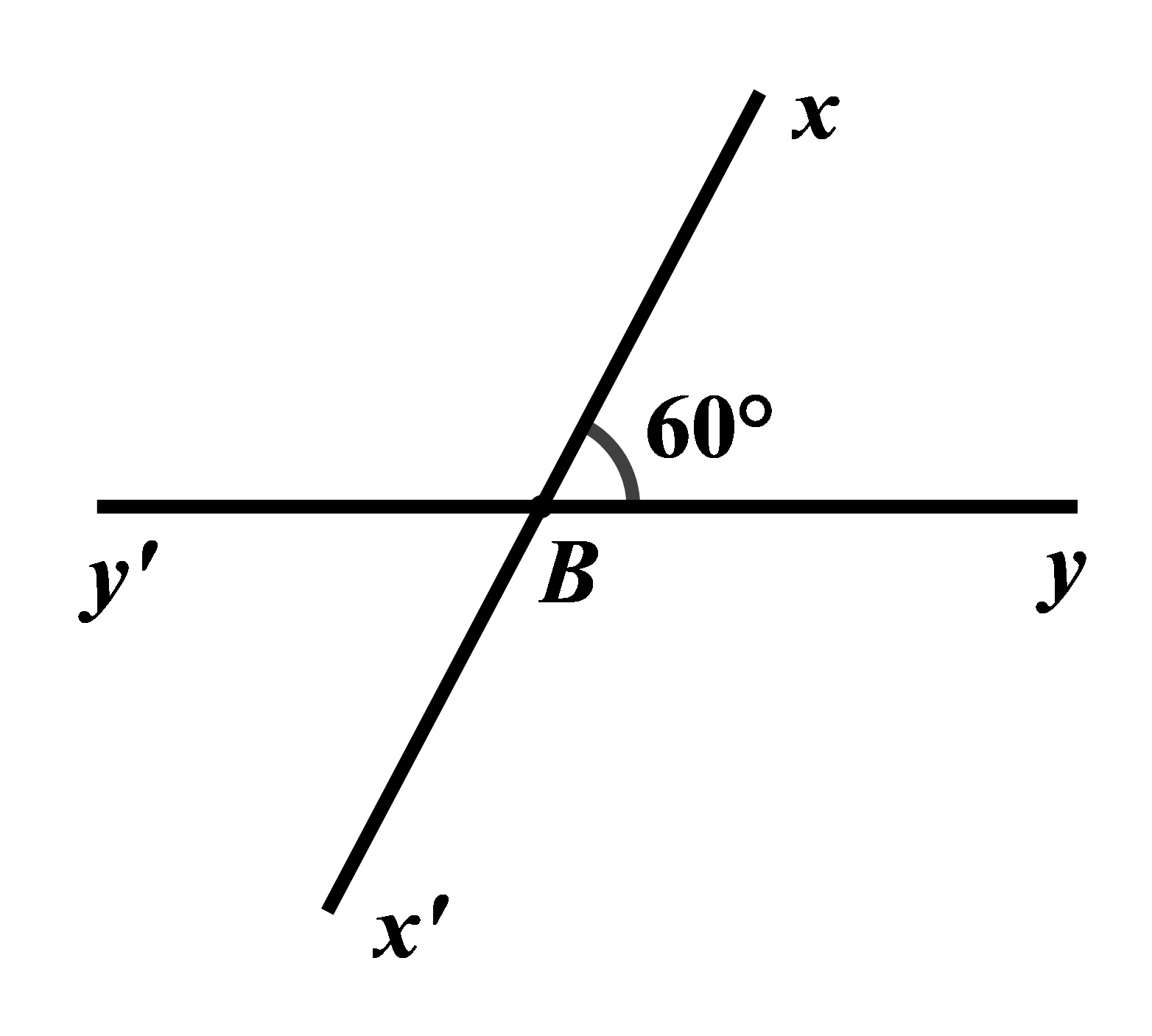






Danh sách bình luận