Đề thi học kì 2 Toán 7 - Đề số 2 - Chân trời sáng tạoTải về I. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài I. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1. Trong trò chơi gieo 2 đồng xu, các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là 4. Nếu k là số kết quả thuận lợi cho biến cố thì xác suất của biến cố đó bằng A. k B. 2k C. \(\dfrac{k}{4}\) D. \(\dfrac{4}{k}\) Câu 2. Biết 7x = 4y và y – x = 24. Khi đó, giá trị của x, y là A. x = −56, y = −32; B. x = 32, y = 56; C. x = 56, y = 32; D. x = 56, y = −32. Câu 3. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu? A. –6; B. 0; C. –9; D. –1. Câu 4. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng: A. –32; B. 32; C. –2; D. 2. Câu 5. Một tam giác có ba góc có số đo tỉ lệ với 3,4,5. Số đo ba góc của tam giác lần lượt là: A. 450; 600; 750; B. 300; 600; 900; C. 200; 600; 1000; D. Một kết quả khác. Câu 6. Hệ số tự do của đa thức M = -8x2 – 4x + 3 – 2x5 là A. -2; B. 4; C. 3; D. 5. Câu 7. Cho hai đa thức P(x) = 6x3 − 3x2 − 2x + 4 và G(x) = 5x2 − 7x + 9. Giá trị P(x) − G(x) bằng A. x2 − 9x +13; B. 6x3 − 8x2 + 5x −5; C. x3 − 8x2 + 5x −5; D. 5x3 − 8x2 + 5x +13. Câu 8. Trong các giá trị sau đây, đâu là nghiệm của đa thức 5x2 − 3x – 2? A. \(x = 1\) và \(x = \frac{2}{5}\) B. \(x = - 1\) và \(x = \frac{2}{5}\) C. \(x = 1\) và \(x = \frac{{ - 2}}{5}\) D. \(x = - 1\) và \(x = \frac{{ - 2}}{5}\). Câu 9. Cho tam giác MNP có: \(\widehat N = 70^\circ ;\widehat P = 55^\circ \). Khẳng định nào sau đây là đúng? A. NP < MN; B. NP = MN; C. NP > MN; D. Không đủ dữ kiện so sánh. Câu 10. Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB > AC} \right)\). Tia phân giác của góc \(B\) cắt \(AC\) ở \(D\). Kẻ \(DH\) vuông góc với \(BC\).Chọn câu đúng. A. \(BH = BD\) B. \(BH > BA\) C. \(BH < BA\) D. \(BH = BA\) Câu 11. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác? A. 18cm; 28cm; 10cm; B. 5cm; 4cm; 6cm; C. 15cm; 18cm; 20cm; D. 11cm; 9cm; 7cm. Câu 12. Cho tam giác ABC vuông tại A. Khẳng định nào dưới đây là đúng? A. A là tâm đường tròn ngoại tiếp tam giác ABC. B. A là trọng tâm tam giác ABC. C. A là trực tâm tam giác ABC. D. A là tâm đường tròn nội tiếp tam giác ABC. II. PHẦN TỰ LUẬN (7,0 điểm) Bài 1. (1,5 điểm) Tính chu vi của hình chữ nhật biết rằng chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với \(5\,\,;\,\,3\) và hai lần chiều dài hơn ba lần chiều rộng là 8 cm. Bài 2. (1,5 điểm) Cho hai đa thức: \(M\left( x \right) = 2 - 5{x^2} + 3{x^4} - 4{x^2} + 3x + {x^4} - 4{x^6} - 7x\) \(N\left( x \right) = {\rm{ \;}} - 1 + 5{x^6} - 6{x^2} - 5 - 9{x^6} + 4{x^4} - 3{x^2}\) a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến. b) Tìm đa thức \(H\left( x \right)\) và \(G\left( x \right)\) biết \(H\left( x \right) = M\left( x \right) + N\left( x \right)\) và \(G\left( x \right) = M\left( x \right) - N\left( x \right)\). c) Tìm nghiệm của đa thức \(G\left( x \right)\). Bài 3. (3,5 điểm) Cho \(\Delta ABC\) vuông tại \(A\), phân giác BD\(\left( {D \in AC} \right)\). Kẻ DEvuông góc với BC \(\left( {E \in BC} \right)\). a) Chứng minh: \(\Delta ABD = \Delta EBD\). b) Kẻ \(AH \bot BC,{\mkern 1mu} \left( {H \in BC} \right)\), AH cắt BD tại I. Chứng minh rằng AH song song với DE và \(\Delta AID\) cân. c) Chứng minh rằng AE là phân giác \(\widehat {HAC}\). d) \(\Delta ABC\) cần thêm điều kiện gì để \(DC = 2AI\). Bài 4. (0,5 điểm) Cho đa thức \(f\left( x \right)\) thỏa mãn \(f\left( x \right) + x.f\left( { - x} \right) = x + 1\) với mọi giá trị của \(x\). Tính \(f\left( 1 \right)\). Lời giải I. Trắc nghiệm
Câu 1. Phương pháp Xác suất của biến cố trong trò chơi gieo xúc xắc bằng tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc. Cách giải: Nếu k là số kết quả thuận lợi cho biến cố thì xác suất của biến cố đó bằng \(\frac{k}{4}\) Chọn C. Câu 2. Phương pháp Áp dụng tính chất dãy tỉ số bằng nhau Lời giải Vì 7x = 4y nên \(\dfrac{x}{4} = \dfrac{y}{7}\) Áp dụng tính chất dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{4} = \dfrac{y}{7} = \dfrac{{y - x}}{{7 - 4}} = \dfrac{{24}}{3} = 8\) Do đó x = 4 . 8 = 32; y = 7 . 8 = 56. Chọn B. Câu 3. Phương pháp Đại lượng \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(k\) thì \(y = kx\) Lời giải Khi x = - 3 thì \(y = kx = 2.( - 3) = - 6\) Chọn A. Câu 4. Phương pháp Tính chất hai đại lượng tỉ lệ nghịch: tích 2 giá trị tương ứng của 2 đại lượng luôn không đổi (bằng hệ số tỉ lệ) Cách giải: Hệ số tỉ lệ là: -12 . 8 = -96. Khi x = 3 thì y = -96 : 3 = -32. Chọn A Câu 5. Phương pháp Áp dụng: Định lí Tổng định lí 3 góc trong một tam giác bằng 180 độ. Tính chất của dãy tỉ số bằng nhau Cách giải: Gọi số đo 3 góc của tam giác lần lượt là a,b,c. Vì tổng 3 góc trong một tam giác là 180 độ nên \(a + b + c = 180^\circ \). Do số đo ba góc tỉ lệ với 3;4;5 nên \(\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5}\). Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\begin{array}{l}\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5} = \dfrac{{a + b + c}}{{3 + 4 + 5}} = \dfrac{{180}}{{12}} = 15\\ \Rightarrow a = 15.3 = 45;\\b = 15.4 = 60;\\c = 15.5 = 75.\end{array}\) Chọn A. Câu 6 Phương pháp Hệ số tự do của đa thức thu gọn là hệ số của hạng tử không chứa biến trong đa thức. Cách giải: M = -8x2 – 4x + 3 – 2x5 có hệ số tự do là 3. Chọn C Câu 7. Ta có: P(x) − G(x) = (6x3 − 3x2 − 2x + 4) − (5x2 − 7x + 9) = 6x3 − 3x2 − 2x + 4 − 5x2 + 7x − 9 = 6x3 + (−3x2 − 5x2) + (−2x + 7x) + (4 − 9) = 6x3 − 8x2 + 5x − 5. Vậy P(x) − G(x) = 6x3 − 8x2 + 5x −5. Chọn B. Câu 8. Phương pháp Thay lần lượt các giá trị của x vào đa thức. Khi x = a, đa thức có giá trị bằng 0 thì a là nghiệm của đa thức. Lời giải +) Thay \(x = 1\) vào đa thức 5x2 − 3x – 2, ta có: \({5.1^2} - 3.1 - 2 = 0\) Do đó, \(x = 1\) là nghiệm của đa thức 5x2 − 3x – 2. +) Thay \(x = - 1\) vào đa thức 5x2 − 3x – 2, ta có: \(5.{\left( { - 1} \right)^2} - 3.\left( { - 1} \right) - 2 = 5 + 3 - 2 = 6\) Do đó, \(x = - 1\) không là nghiệm của đa thức 5x2 − 3x – 2. +) Thay \(x = \frac{2}{5}\) vào đa thức 5x2 − 3x – 2, ta có: \(5.{\left( {\frac{2}{5}} \right)^2} - 3.\frac{2}{5} - 2 = 5.\frac{4}{{25}} - \frac{6}{5} - 2 = \frac{4}{5} - \frac{6}{5} - 2 = \frac{{ - 12}}{5}\) Do đó, \(x = \frac{2}{5}\) không là nghiệm của đa thức 5x2 − 3x – 2. Thay \(x = \frac{{ - 2}}{5}\) vào đa thức 5x2 − 3x – 2, ta có: \(5.{\left( {\frac{{ - 2}}{5}} \right)^2} - 3.\frac{{ - 2}}{5} - 2 = 0\) Do đó, \(x = \frac{{ - 2}}{5}\) là nghiệm của đa thức 5x2 − 3x – 2. Vậy \(x = 1\) và \(x = \frac{{ - 2}}{5}\) là hai nghiệm của đa thức 5x2 − 3x – 2. Chọn C. Câu 9. Phương pháp: Áp dụng định lí tổng ba góc trong tam giác, tính góc M. Dựa vào quan hệ giữa cạnh và góc đối diện trong tam giác. Cách giải:
Xét tam giác MNP có: \(\widehat M + \widehat N + \widehat P = 180^\circ \) (định lí tổng ba góc trong một tam giác) \( \Rightarrow \widehat M = 180^\circ - \widehat N - \widehat P = 180^\circ - 70^\circ - 55^\circ = 55^\circ \) Ta được: \(\widehat M = \widehat P\) Mà cạnh NP là cạnh đối của góc M, MN là cạnh đối của góc P. Vậy NP = MN. Chọn B. Câu 10: Phương pháp: Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – góc nhọn, từ đó suy ra cặp cạnh tương ứng bằng nhau. Cách giải:
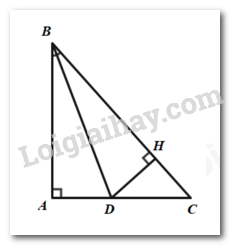
Xét \(\Delta BAD\) và \(\Delta BHD\) có: \(\angle BAD = \angle BHD = 90^\circ \) \(BD\) chung \(\angle ABD = \angle HBD\) (vì \(BD\) là tia phân giác \(\angle B\)) \( \Rightarrow \Delta ABD = \Delta HBD\) (cạnh huyền – góc nhọn) \( \Rightarrow BA = BH\)(hai cạnh tương ứng). Chọn D. Câu 11. Phương pháp: Bất đẳng thức tam giác: Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu không thì bộ 3 độ dài đó không tạo được thành tam giác. Cách giải: Vì 18 + 10 = 28 nên không thỏa mãn bất đẳng thức tam giác. Do đó, bộ ba độ dài đoạn thẳng 18 cm; 28 cm; 10 cm không thể tạo thành một tam giác. Chọn A. Câu 12. Phương pháp Vẽ hình và nhận xét A là giao điểm của hai đường thẳng nào? Hai đường thẳng ấy có quan hệ như thế nào với tam giác ABC. Cách giải: Vì \(AB \bot AC\) nên AB, AC là hai đường cao. Suy ra A là giao điểm của hai đường cao. Vậy A là trực tâm tam giác ABC. Đáp số: A là trực tâm tam giác ABC. Chọn C. II. PHẦN TỰ LUẬN (7,0 điểm) Câu 1 Phương pháp: Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là \(x,y\) (cm) (điều kiện: \(x,y > 0\)) Áp dụng tính chất của dãy tỉ số bằng nhau. Cách giải: Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là \(x,y\) (cm) (điều kiện: \(x,y > 0\)) Theo đề bài: chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với \(5\,\,;\,\,3\) nên ta có: \(\dfrac{x}{5} = \dfrac{y}{3}\) Hai lần chiều dài hơn ba lần chiều rộng là \(8\) cm nên \(2x - 3y = 8\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{5} = \dfrac{y}{3} = \dfrac{{2x}}{{10}} = \dfrac{{3y}}{9} = \dfrac{{2x - 3y}}{{10 - 9}} = \dfrac{8}{1} = 8\) Khi đó, \(\dfrac{x}{5} = 8 \Rightarrow x = 40\) (tmđk) \(\dfrac{y}{3} = 8 \Rightarrow y = 24\) (tmđk) Chu vi của hình chữ nhật là: \(2\left( {x + y} \right) = 2\left( {40 + 24} \right) = 128\) (cm) Bài 2. + Ta có thể mở rộng cộng (trừ) các đa thức dựa trên quy tắc “dấu ngoặc” và tính chất của các phép toán trên số. + Đối với đa thức một biến đã sắp xếp còn có thể cộng (trừ) bằng cách đặt tính theo cột dọc tương tự cộng (trừ) các số. + \(x = a\) được gọi là nghiệm của \(P\left( x \right)\)nếu: \(P\left( a \right) = 0\) + Với các đa thức bậc cao, ta thường biến đổi để đưa về tích của các đơn thức rồi tìm nghiệm. + \(A.B = 0 \Rightarrow A = 0\)hoặc \(B = 0\). Cách giải: \(M\left( x \right) = 2 - 5{x^2} + 3{x^4} - 4{x^2} + 3x + {x^4} - 4{x^6} - 7x\) \(N\left( x \right) = {\rm{ \;}} - 1 + 5{x^6} - 6{x^2} - 5 - 9{x^6} + 4{x^4} - 3{x^2}\) a) Ta có: \(\begin{array}{*{20}{l}}{M\left( x \right) = 2 - 5{x^2} + 3{x^4} - 4{x^2} + 3x + {x^4} - 4{x^6} - 7x}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4{x^6} + \left( {3{x^4} + {x^4}} \right) + \left( { - 5{x^2} - 4{x^2}} \right) + \left( {3x - 7x} \right) + 2}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4{x^6} + 4{x^4} - 9{x^2} - 4x + 2}\end{array}\) \(\begin{array}{*{20}{l}}{N\left( x \right) = {\rm{ \;}} - 1 + 5{x^6} - 6{x^2} - 5 - 9{x^6} + 4{x^4} - 3{x^2}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \left( {5{x^6} - 9{x^6}} \right) + 4{x^4} + \left( { - 6{x^2} - 3{x^2}} \right) + \left( { - 1 - 5} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4{x^6} + 4{x^4} - 9{x^2} - 6}\end{array}\) b) Ta có: \(\begin{array}{*{20}{l}}{H\left( x \right) = M\left( x \right) + N\left( x \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = ( - 4{x^6} + 4{x^4} - 9{x^2} - 4x + 2) + ( - 4{x^6} + 4{x^4} - 9{x^2} - 6)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \left( { - 4{x^6} - 4{x^6}} \right) + \left( {4{x^4} + 4{x^4}} \right) + \left( { - 9{x^2} - 9{x^2}} \right) - 4x + \left( {2 - 6} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 8{x^6} + 8{x^4} - 18{x^2} - 4x - 4}\end{array}\) \(\begin{array}{*{20}{l}}{G\left( x \right) = M\left( x \right) - N\left( x \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = ( - 4{x^6} + 4{x^4} - 9{x^2} - 4x + 2) - \left( { - 4{x^6} + 4{x^4} - 9{x^2} - 6} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4{x^6} + 4{x^4} - 9{x^2} - 4x + 2 + 4{x^6} - 4{x^4} + 9{x^2} + 6}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \left( { - 4{x^6} + 4{x^6}} \right) + \left( {4{x^4} - 4{x^4}} \right) + \left( { - 9{x^2} + 9{x^2}} \right) - 4x + \left( {2 + 6} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\rm{ \;}} - 4x + 8}\end{array}\) c) \(G\left( x \right) = 0 \Rightarrow {\rm{ \;}} - 4x + 8 = 0 \Rightarrow {\rm{ \;}} - 4x = {\rm{ \;}} - 8 \Rightarrow x = 2\). Bài 3. Phương pháp: + Sử dụng các cách chứng minh hai tam giác bằng nhau. + Sử dụng tính chất của các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. + Các định lí từ vuông góc tới song song. + Tính chất các đường cao, đường phân giác, đường trung trực trong tam giác cân. Cách giải:
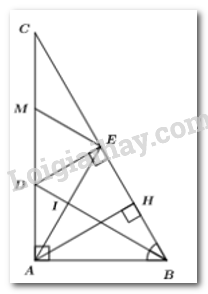
a) Xét hai tam giác vuông\(\Delta ABD\)và\(\Delta EBD\)có: + BD chung + \(\angle ABD = \angle EBD\) (vìBDlà tia phân giác của \(\angle ABC\)) \( \Rightarrow \Delta ABD = \)\(\Delta EBD\) (cạnh huyền – góc nhọn) (đpcm) b) Vì \(\left\{ {\begin{array}{*{20}{l}}{AH \bot BC{\mkern 1mu} \left( {gt} \right)}\\{DE \bot BC{\mkern 1mu} \left( {gt} \right)}\end{array}} \right. \Rightarrow AH//DE\) (từ vuông góc đến song song) \( \Rightarrow \widehat {AID} = \widehat {IDE}\) (2 góc so le trong) (1) Vì \(\Delta ABD = \Delta EBD\) (câu a) nên \(\widehat {ADB} = \widehat {BDE}\) (2 góc tương ứng) hay \(\widehat {ADI} = \widehat {IDE}\) (2) Từ (1) và (2) \( \Rightarrow \widehat {AID} = \widehat {ADI}\). Do đó \(\Delta AID\) cân tại \(A\). (đpcm) c) Vì \(AH//DE\) (cmt) nên \(\widehat {HAE} = \widehat {AED}\) (2 góc so le trong) (3) Vì \(\Delta ABD = \Delta EBD\) (câu a) nên \(AD = DE\) (2 cạnh tương ứng) \( \Rightarrow \Delta ADE\) cân tại D. \( \Rightarrow \widehat {DAE} = \widehat {DEA}\) (2 góc tương ứng) (4) Từ (3) và (4) \( \Rightarrow \widehat {HAE} = \widehat {DAE}\)\( \Rightarrow AE\) là tia phân giác của \(\widehat {HAC}\) (đpcm). d) Vì \(\Delta AID\) cân tại \(A\)\( \Rightarrow AI = AD\), lại có \(AD = DE\) (cmt) \( \Rightarrow AI = DE\) Nếu \(DC = 2AI\) \( \Rightarrow DC = 2DE\). Gọi \(M\) là trung điểm DC\( \Rightarrow DM = MC\). Xét tam giác vuông DEC có EM là đường trung tuyến \( \Rightarrow EM = DM = MC\) \( \Rightarrow \Delta DEM\) là tam giác đều \( \Rightarrow \widehat {EDC} = {60^\circ }\) (tính chât tam giác đều). Xét tam giác DEC vuông tại \(E\) có \(\widehat {EDC} = {60^\circ }\)\( \Rightarrow \widehat {DCE} = {30^\circ }\) hay \(\widehat {ACB} = {30^\circ }\). Vậy để \(DC = 2AI\) thì tam giác ABC có thêm điều kiện là \(\widehat {ACB} = {30^\circ }\). Bài 4. Phương pháp: Xét với \(x = - 1\), ta tìm được mối liên hệ của \(f\left( { - 1} \right)\) và \(f\left( 1 \right)\) Xét với \(x = 1\), ta tìm được \(f\left( 1 \right)\). Cách giải: + Với \(x = - 1\), ta có: \(f\left( { - 1} \right) + \left( { - 1} \right).f\left( 1 \right) = - 1 + 1\) \(\begin{array}{l} \Rightarrow f\left( { - 1} \right) - f\left( 1 \right) = 0\\ \Rightarrow f\left( { - 1} \right) = f\left( 1 \right)\end{array}\) + Với \(x = 1\), ta có: \(f\left( 1 \right) + 1.f\left( { - 1} \right) = 1 + 1\) \( \Rightarrow f\left( 1 \right) + f\left( { - 1} \right) = 2\) Suy ra, \(f\left( 1 \right) + f\left( 1 \right) = 2\) \(\begin{array}{l} \Rightarrow 2f\left( 1 \right) = 2\\ \Rightarrow f\left( 1 \right) = 1\end{array}\) Vậy \(f\left( 1 \right) = 1\)
|




















Danh sách bình luận