Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 16Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Căn bậc hai số học của 36 là:
Câu 2 :
Số nào là số vô tỉ trong các số sau:
Câu 3 :
Cho \(\left| x \right| = 9\) thì giá trị của x là:
Câu 5 :
Qua điểm M nằm ngoài đường thẳng a, ... đường thẳng song song với đường thẳng a. Hãy điền vào chỗ “…” để được khẳng định đúng.
Câu 6 :
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn môn thể thao ưa thích nhất trong bốn môn: Bóng đá, Cầu lông, Bóng bàn, Bóng chuyền của học sinh khối 7 ở trường A. Mỗi học sinh chỉ được chọn một môn thể thao khi được hỏi ý kiến. Hỏi số học sinh chọn môn Bóng đá và Cầu lông chiếm bao nhiêu phần trăm?
Câu 7 :
Quan sát hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ ở hình bên. Cho biết mặt bên ABB’A’ là hình gì?
Câu 8 :
Diện tích xung quanh của hình lập phương có cạnh dài 5m là:
Câu 9 :
Giá trị của \(\sqrt {54756} \) là:
Câu 10 :
Bể cá cảnh trong hình vẽ bên có dạng hình lập phương với độ dài cạnh là 40cm. Thể tích của bể cá là:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Căn bậc hai số học của 36 là:
Đáp án : C Phương pháp giải :
Căn bậc hai số học của một số a không âm là số x không âm sao cho \({x^2} = a\). Lời giải chi tiết :
Căn bậc hai số học của 36 là \(\sqrt {36} = 6\). Đáp án C
Câu 2 :
Số nào là số vô tỉ trong các số sau:
Đáp án : B Phương pháp giải :
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn. Lời giải chi tiết :
Số \( - \sqrt 5 \) là số vô tỉ. Các số \(\frac{5}{6};0;6,5\) là các số hữu tỉ. Đáp án B
Câu 3 :
Cho \(\left| x \right| = 9\) thì giá trị của x là:
Đáp án : D Phương pháp giải :
Nếu \(\left| x \right| = a\) thì \(x = a\) hoặc \(x = - a\) Lời giải chi tiết :
Với \(\left| x \right| = 9\) thì \(x = 9\) hoặc \(x = - 9\). Đáp án D
Đáp án : C Phương pháp giải :
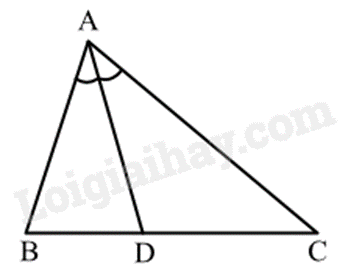
Tia phân giác của một góc là tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau. Lời giải chi tiết :
Tia AD là tia phân giác của góc BAC. Đáp án C
Câu 5 :
Qua điểm M nằm ngoài đường thẳng a, ... đường thẳng song song với đường thẳng a. Hãy điền vào chỗ “…” để được khẳng định đúng.
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về tiên đề Euclid về đường thẳng song song. Lời giải chi tiết :
Theo tiên đề Euclid: “Qua điểm M nằm ngoài đường thẳng a, chỉ có một đường thẳng song song với đường thẳng a.” Đáp án A
Câu 6 :
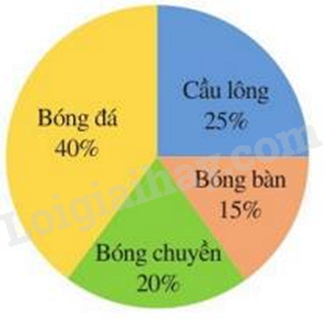
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn môn thể thao ưa thích nhất trong bốn môn: Bóng đá, Cầu lông, Bóng bàn, Bóng chuyền của học sinh khối 7 ở trường A. Mỗi học sinh chỉ được chọn một môn thể thao khi được hỏi ý kiến. Hỏi số học sinh chọn môn Bóng đá và Cầu lông chiếm bao nhiêu phần trăm?
Đáp án : B Phương pháp giải :
Quan sát biểu đồ để xác định số phần trăm tương ứng với số học sinh chọn môn Bóng đá và Cầu lông. Lời giải chi tiết :
Số học sinh chọn môn Bóng đá và Cầu lông chiếm số phần trăm là: 40% + 25% = 65%. Đáp án B
Câu 7 :
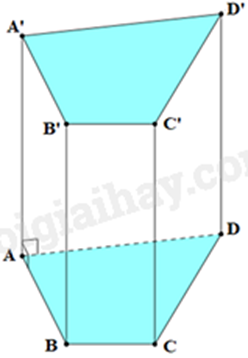
Quan sát hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ ở hình bên. Cho biết mặt bên ABB’A’ là hình gì?
Đáp án : C Phương pháp giải :
Hình lăng trụ đứng tứ giác có hai đáy là hình tứ giác và các mặt bên là hình chữ nhật. Lời giải chi tiết :
Mặt bên ABB’A’ là hình chữ nhật. Đáp án C
Câu 8 :
Diện tích xung quanh của hình lập phương có cạnh dài 5m là:
Đáp án : D Phương pháp giải :
Công thức tính diện tích xung quanh của hình lập phương là: \({S_{xq}} = 4{a^2}\) (a là độ dài cạnh) Lời giải chi tiết :
Diện tích xung quanh của hình lập phương là: \({S_{xq}} = {4.5^2} = 100\left( {{m^2}} \right)\) Đáp án D
Câu 9 :
Giá trị của \(\sqrt {54756} \) là:
Đáp án : B Phương pháp giải :
Sử dụng máy tính cầm tay để tính giá trị của \(\sqrt {54756} \). Lời giải chi tiết :
Ta có: \(\sqrt {54756} = 234\). Đáp án B
Câu 10 :
Bể cá cảnh trong hình vẽ bên có dạng hình lập phương với độ dài cạnh là 40cm. Thể tích của bể cá là:
Đáp án : A Phương pháp giải :
Công thức tính thể tích của hình lập phương: \(V = {a^3}\) với a là độ dài cạnh của hình lập phương. Lời giải chi tiết :
Thể tích của bể cá là: \(V = {40^3} = 64000\left( {c{m^3}} \right)\) Đáp án A
Đáp án : B Phương pháp giải :
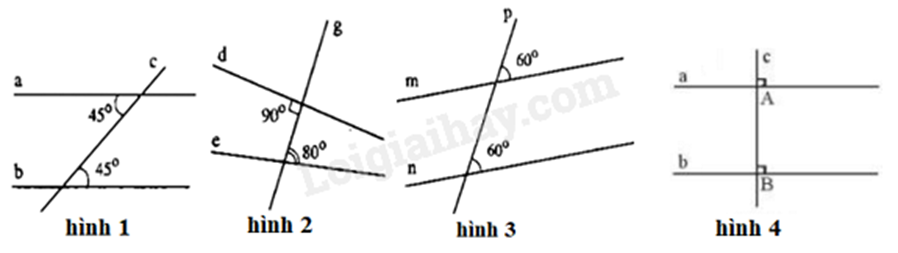
Hai đường thẳng song song nếu: + hai góc so le trong bằng nhau. + hai góc đồng vị bằng nhau. Lời giải chi tiết :
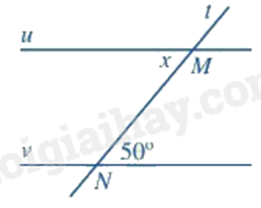
- Hình 1 có hai góc so le trong bằng nhau \(\left( { = 45^\circ } \right)\) nên có a và b là hai đường thẳng song song. - Hình 2 không có hai góc nào bằng nhau nên không có hai đường thẳng song song. - Hình 3 có hai góc đồng vị bằng nhau \(\left( { = 60^\circ } \right)\) nên có m và n là hai đường thẳng song song. - Hình 4 có góc A và góc B bằng nhau \(\left( { = 90^\circ } \right)\) nên a và b song song với nhau (do cùng vuông góc với đường thẳng c). Đáp án B
Đáp án : B Phương pháp giải :
Sử dụng tính chất của hai đường thẳng song song: Nếu hai đường thẳng song song thì: + các cặp góc so le trong bằng nhau + các cặp góc đồng vị bằng nhau. Lời giải chi tiết :
Vì u // v nên \(x = 50^\circ \) (hai góc so le trong). Đáp án B
II. Tự luận
Phương pháp giải :
Áp dụng quy tắc cộng, trừ, nhân, chia với số hữu tỉ. b) Sử dụng tính chất chia hai lũy thừa có cùng cơ số. c) Thực hiện phép tính trong ngoặc sau đó tính lũy thừa và rút gọn. Lời giải chi tiết :
a) \(\frac{1}{2} + \frac{2}{3} - \frac{4}{5}\)\( = \frac{{15 + 20 - 24}}{{30}} = \frac{{11}}{{30}}\) b) \(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^9}:{\left( {\frac{1}{3}} \right)^7} - 2\)\(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^{9 - 7}} - 2\)\( = \frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^2} - 2\)\( = \frac{{17}}{9} + \frac{1}{9} - 2\)\( = 2 - 2\)\( = 0\) c) \(\left( {1 + \frac{1}{2} + \frac{1}{3}} \right){\left( {\frac{4}{5} - \frac{3}{4}} \right)^2}\)\( = \left( {\frac{{6 + 3 + 2}}{6}} \right){\left( {\frac{{16 - 15}}{{20}}} \right)^2}\)\( = \frac{{11}}{6}.{\left( {\frac{1}{{20}}} \right)^2}\)\( = \frac{{11}}{6}.\frac{1}{{400}}\)\( = \frac{{11}}{{2400}}\) Phương pháp giải :
Áp dụng quy tắc chuyển vế đổi dấu. b) Đưa về dạng \(\left| A \right| = B\), chia hai trường hợp: A = B hoặc A = -B. Lời giải chi tiết :
a) \(\frac{2}{5}x - \frac{1}{2} = \frac{{ - 3}}{5}\) \(\begin{array}{l}\frac{2}{5}x = \frac{{ - 3}}{5} + \frac{1}{2}\\\frac{2}{5}x = \frac{{ - 1}}{{10}}\\x = \frac{{ - 1}}{{10}}:\frac{2}{5}\\x = \frac{{ - 1}}{4}\end{array}\) Vậy \(x = \frac{{ - 1}}{4}\). b) \(\left| {x - \frac{1}{2}} \right| = \frac{2}{3}\) \(x - \frac{1}{2} = \frac{2}{3}\) hoặc \(x - \frac{1}{2} = - \frac{2}{3}\) \(x = \frac{2}{3} + \frac{1}{2}\) hoặc \(x = - \frac{2}{3} + \frac{1}{2}\) \(x = \frac{7}{6}\) hoặc \(x = \frac{{ - 1}}{6}\) Vậy \(x \in \left\{ {\frac{7}{6};\frac{{ - 1}}{6}} \right\}\) Phương pháp giải :
Áp dụng công thức tính diện tích xung quanh của hình hộp chữ nhật để tính diện tích cần sơn chiếc thùng: Sxq = Cđáy.chiều cao. Số ki-lô-gam sơn = Sxq : 4. Lời giải chi tiết :
Diện tích cần sơn là: \(2.\left( {2 + 1,5} \right).2 = 14\left( {{m^2}} \right)\) Số ki-lô-gam sơn cần dùng là: \(14:4 = 3,5\left( {kg} \right)\) Vậy người thợ cần 3,5kg sơn để sơn bên ngoài các mặt xung quanh chiếc thùng đó. Phương pháp giải :
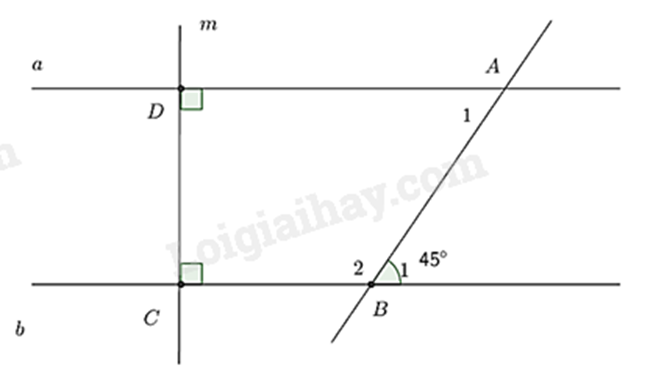
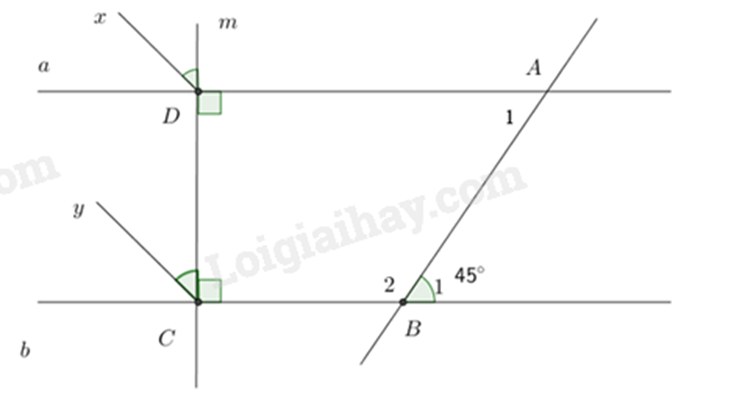
a) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song với nhau. b) Áp dụng tính chất hai góc kề bù có tổng bằng \(180^\circ \) và hai đường thẳng song song thì hai góc so le trong bằng nhau. c) Chứng minh hai góc ở vị trí đồng vị bằng nhau nên Dx // Cy. Lời giải chi tiết :
a) Ta có: \(a \bot m\) (gt), \(b \bot m\) (gt) nên a // b. b) Ta có: \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (hai góc kề bù) \(45^\circ + \widehat {{B_2}} = 180^\circ \) suy ra \(\widehat {{B_2}} = 180^\circ - 45^\circ = 135^\circ \). Vì a // b nên \(\widehat {{B_1}} = \widehat {{A_1}}\) (hai góc so le trong) Mà \(\widehat {{B_1}} = 45^\circ \) nên \(\widehat {{A_1}} = 45^\circ \). c) Vì Dx là tia phân giác của \(\widehat {aDm}\) (gt) nên \(\widehat {xDm} = 90^\circ :2 = 45^\circ \) Vì \(Cy\) là tia phân giác của \(\widehat {bCD}\) (gt) nên \(\widehat {yCD} = 90^\circ :2 = 45^\circ \) Do đó \(\widehat {xDm} = \widehat {yCD}\) Mà hai góc này ở vị trí đồng vị nên Dx // Cy. Phương pháp giải :
Áp dụng bài toán tìm m% của a theo công thức: m%.a Lời giải chi tiết :
Số tiền bạn An phải trả khi mua đôi giày ứng với số phần trăm là: 100% - 20% = 80% Số tiền bạn An phải trả khi mua đôi giày là: 400 000.80% = 320 000 (đồng) Vậy giá của đôi giày sau khi giảm giá là 320 000 đồng.
|






















Danh sách bình luận